1.2.2. Связь между векторным и координатным декартовым способами задания движения мт

Разлагая радиус-вектор МТ на составляющие, параллельные осям декартовой системы координат, получим искомую связь:

. (1.5)

1.2.3. Траектория мт

Уравнения (1.4) являются также уравнениями траектории МТ в параметрической форме, где параметром является время t.

Для того чтобы получить уравнение траектории МТ в явной форме необходимо из соотношений (1.4) исключить время t.

1.2.4. Скорость мт

Разлагая скорость МТ на составляющие, параллельные осям декартовой системы координат, получим:

, (1.6)

где V_x, V_y, V_z — проекции скорости МТ на соответствующие оси декартовой системы координат.

Учитывая соотношение (1.5), на основании соотношения (1.2) получим:

. (1.7)

Сравнивая соотношения (1.6) и (1.7), можно записать:

(1.8)

Используя соотношения (1.8), определяются модуль скорости МТ и направляющие косинусы углов, которые составляет скорость МТ с осями декартовой системы координат:

(1.9)

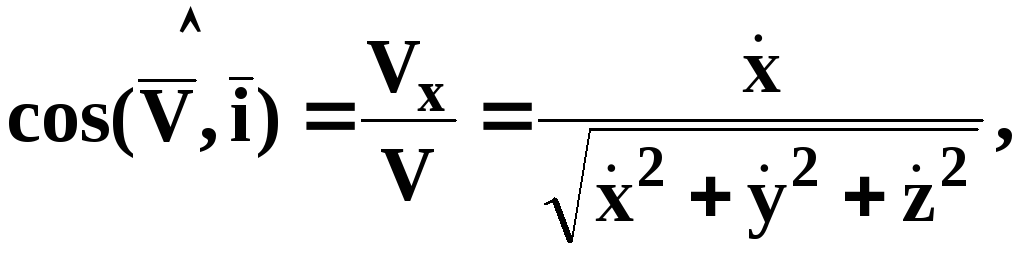
1.2.5. Ускорение мт

Разлагая ускорение МТ на составляющие, параллельные осям декартовой системы координат, получим:

, (1.10)

где W_x, W_y, W_z — проекции ускорения МТ на оси декартовой системы координат.

Учитывая соотношения (1.5) и (1.6), на основании формулы (1.3) получим:

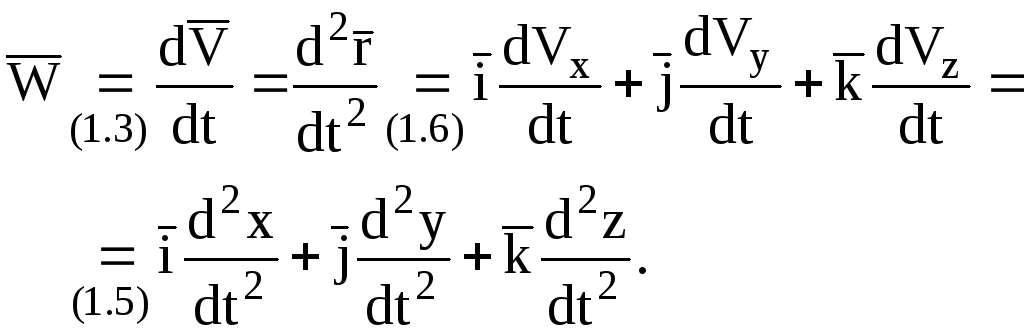(1.11)

Сравнивая соотношение (1.10) и (1.11), можно записать:

(1.12)

Используя формулы (1.12), определяются модуль ускорения МТ и направляющие косинусы углов, которые составляет ускорение МТ с осями декартовой системы координат:

(1.13)

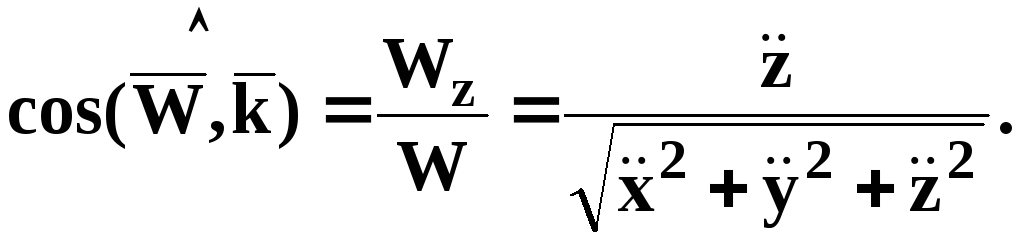
1.3. Естественный способ задания движения мт

1.3.1. Уравнение движения МТ

При естественном способе задания движения МТ необходимо знать:

• траекторию движения МТ,

• начало отсчета длины дуги на траектории — В₀,

• положительное направление отсчета,

• закон движения МТ по траектории в виде зависимости от времени длины дуги s, отсчитываемой от точки В₀ до точки В (уравнение движения), т.е.

s=s(t). (1.14)

Рис. 5

Функция должна быть однозначной, непрерывной и дважды дифференцируемой.

1.3.2. Скорость МТ

Для выражения скорости МТ через s, используя формулу (1.2), после простых преобразований получим:

.

При В₁В, (s0), длина дуги стремится к длине хорды:

.

Направление совпадает с касательной к траектории в точке В.

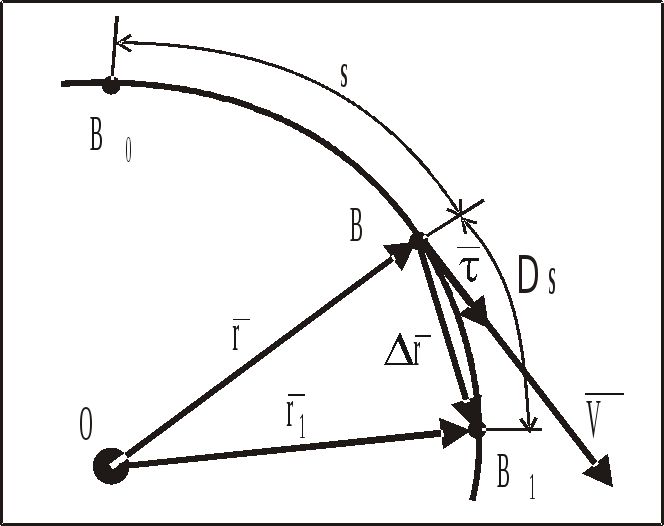
Рис. 6

Таким образом, , где и является единичным вектором касательной, направленным в сторону возрастания длины дуги s (рис.6) и тогда

, (1.15) . (1.16)

1.3.3. Связь между координатным декартовым и

естественным способами задания движения МТ

Даны уравнения движения МТ в виде (1.4):

x=x(t), y=y(t), z=z(t).

Перейдем к естественному способу задания движения МТ.

Для выполнения четырех условий п. 1.3.1 необходимо:

• использовать соотношения (1.4), как уравнения траектории МТ в параметрической форме, где параметром является время t, и, чтобы получить уравнение траектории МТ в явной форме, из него надо исключить время t;

• определить положение МТ в начальный момент времени В₀(x_0, y₀, z₀) на траектории, подставив в уравнение (1.4) t=0:

x₀=x(0), y₀=y(0), z₀=z(0);

• определить положительное направление отсчета длины дуги на траектории МТ, подставив в уравнение (1.4) момент времени t > 0 (близкое к начальному), изобразить В (x, y, z) на траектории и тогда направление движения по траектории от В₀ к В будет положительным;

• найти s=s(t), используя формулу (1.16) и первое соотношение в выражениях (1.9):

. (1.17)

1.3.4. Элементы дифференциальной геометрии

Для определения ускорения МТ при естественном способе задания движения МТ необходимо знать некоторые сведения из дифференциальной геометрии.

• Кривизна, радиус кривизны и соприкасающаяся плоскость

Проведем в точке В к кривой единичный касательный вектор, а в точке В₁, отстоящей от точки В на расстоянии s по траектории, единичный касательный вектор (рис. 7).

В точку В перенесем параллельно самому себе вектор и обозначим угол между и через .

Рис. 7

Определение: Кривизной кривой – k в точке В называется

. (1.18)

Определение: Радиусом кривизны кривой – _к в точке В называется величина, обратная кривизне кривой в этой точке, т.е.

. (1.19)

• Естественный трехгранник

Определения:

Соприкасающейся плоскостью кривой в точке В называется предельное положение плоскости, проходящей через и , перенесенного параллельно самому себе в точку В₁, при s0 (рис. 8).

Первая естественная ось – это касательная, направленная в сторону возрастания дуговой координаты s с единичным касательным вектором .

Нормальной плоскостью называется плоскость, проходящая через точку В перпендикулярно к (рис. 8).

Линия пересечения соприкасающейся и нормальной плоскостей называется главной нормалью.

Единичный вектор, направленный по главной нормали в сторону вогнутости траектории, называется единичным нормальным вектором .

Рис. 8

Спрямляющей плоскостью называется плоскость, проходящая через точку В перпендикулярно к соприкасающейся и нормальной плоскостям.

Линия пересечения нормальной и спрямляющей плоскостей называется бинормалью.

Единичный вектор, направленный по бинормали в ту сторону, чтобы он составлял правую тройку векторов с векторами и (с конца вектора поворот от к должен быть виден против хода часовой стрелки), называется единичным бинормальным вектором .

Три взаимно перпендикулярные оси, положительные направления которых совпадают с направлениями единичных векторов , , , называются естественными осями. Эти оси вместе с тремя плоскостями: соприкасающейся, нормальной и спрямляющей образуют в точке В естественный трехгранник.

При движении точки по кривой естественный трехгранник движется вместе с точкой, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.

• Производная по скалярному аргументу от вектора постоянного модуля

Пусть (u) - векторная функция скалярного аргумента,

имеющая постоянный модуль: .

На основании определения производной можно записать

.

Так как по условию а(u)=а(u+u), то из равнобедренного треугольника ОВВ₁ (рис. 9) можно определить:

.

Тогда

, здесь .

Если продифференцировать по u выражение =а²=const, получим , т. е. .

Рис. 9

Обозначив через единичный вектор, перпендикулярный к , можно записать:

.

Если скалярным аргументом будет время t, то

. (1.20)

Формулу (1.20) можно выразить векторным произведением:

, (1.21)

где — вектор, равный по модулю , направленный перпендикулярно к плоскости, в которой расположены и так, что поворот от к виден против хода часовой стрелки. Понятие угловой скорости — будет подробно рассмотрено в главе 3 "Вращательное движение НМС вокруг неподвижной оси".