Задача № 1

1.; 2.;

3. ; 4..

1. .

Переменные разделились.

Тогда ;.

Закончить самостоятельно.

2. После замены у = t * x, у = tx + t имеем:

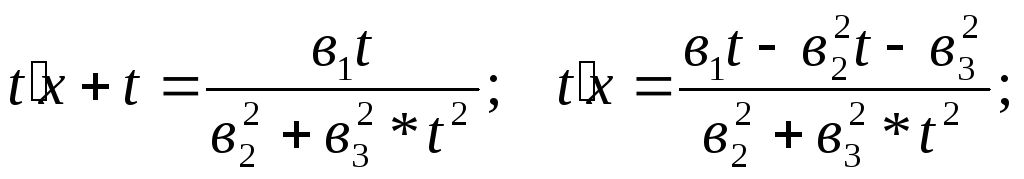
учитывая, что ,

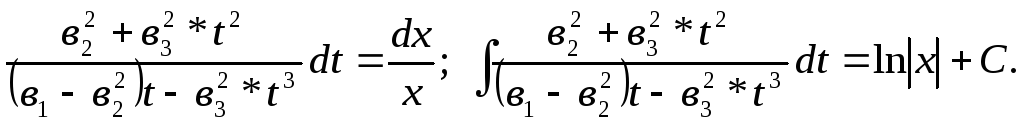
Интеграл слева вычислить самостоятельно.

3. 

Это - линейное уравнение, где ,

у = U * V, y = UV + UV,

- уравнение с разделяющимися переменными. Т. к. то;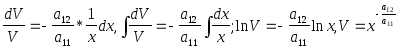

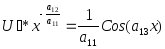- уравнение с разделяющимися переменными.

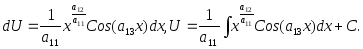Окончательно,

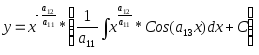- общий интеграл исходного уравнения (последний интеграл вычислить самостоятельно).

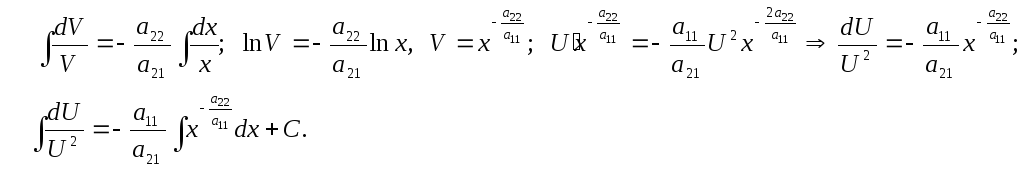
Далее по той же схеме, что и в предыдущем примере (закончить самостоятельно).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2-ГО ПОРЯДКА

Основные определения

Общий вид:

F(x, y, y , y) = 0 (7)

или

y = f (x, y, y). (7)

Начальные условия имеют вид

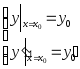. (8)

Функция (9) называется общим решением (7) или (7) в соответствующей области Д (С₁,С₂ - произвольные константы), если при соответствующем выборе С₁ и С₂ эта функция дает частное решение (7), удовлетворяющее (8).

Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами однородные уравнения

Общий вид:

у + а₁у + а₂у = 0 . (13)

Составляем характеристическое уравнение:

к² + а₁к + а₂ = 0. (13)

Пусть к₁, к₂ - его корни. Возможны 3 случая:

а) корни вещественные, различные;

б) корни вещественные, равные: к₁ = к₂ = к (2-кратный корень);

в) корни комплексные, сопряженные к_1,2 = а ± iв, где i = ).

Вид общего решения (13) в каждом из этих случаев запишем в табл. 1 .

Таблица 1

Корни к1, к2	Общее решение (13) ()
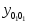(а)	.
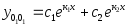(б)	.
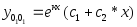(в)	.

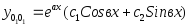Задача № 2

1. у - 4а₁₁² у + 3а₁₁¹у = 0; 2. у + 2а₂₂ у + а₂₂²у = 0;

3. у + а₂₁у = 0; 4. у + а₃₃²у = 0.

1. Характеристическое уравнение: .

Легко находим, что к₁ = 3а₁₁, к₂ = а₁₁ (корни вещественные, различные). Это 1-й случай табл. 1. Тогда - общее решение.

2. Характеристическое уравнение: .

Далее применить табл. 1 и самостоятельно записать у_о.о..

3. Характеристическое уравнение: .

Закончить пример самостоятельно.

4. Характеристическое уравнение: .

Закончить пример самостоятельно.

В следующих примерах найти частные решения д. у. (у_ч.о.), удовлетворяющие заданным начальным условиям.

5. у - 3а₁₂ у + 2а₁₂у = 0, у(1) = в₁, у(1) = в₂;

6. у - а₂₂²у = 0, у(0) = в₂, у(0) = в₃.

5. Характеристическое уравнение:

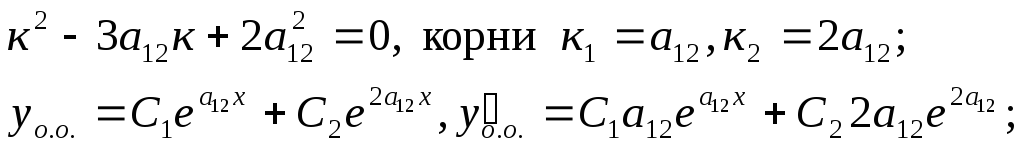
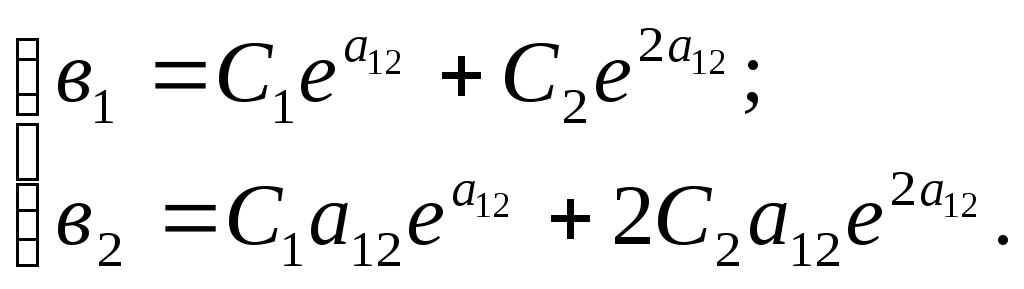
Решить систему, найти С₁, С₂ и у_ч.о..

6. Характеристическое уравнение:

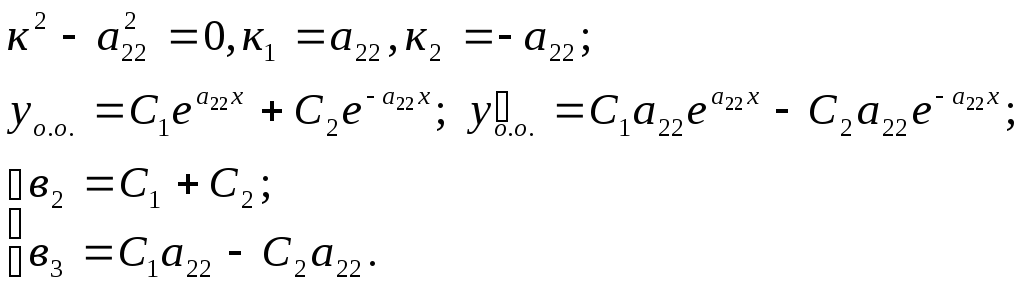
Решить систему, найти С₁, С₂ и у_ч.о..