
- •Интегральное исчисление
- •1. Интегральное исчисление
- •Основные свойства неопределенного интеграла
- •Найти неопределенный интеграл .
- •Метод подстановки
- •Найти неопределенный интеграл .
- •Задача № 8
- •Теорема существования определенного интеграла
- •Вычисление объема тела вращения
- •Задача № 12
- •Двойной интеграл
- •Двойной интеграл в прямоугольных координатах
- •Вычисление двойного интеграла
- •Задача № 13
- •Задача № 14
- •Контрольная работа №4 дифференциальные уравнения
- •Задача № 1
- •Основные определения
- •Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами однородные уравнения
- •Задача № 2
- •Неоднородные уравнения случай специальной правой части
- •Задача № 3
- •Пояснение
- •Контрольная работа
- •Высшей математике (часть 2) Студента(ки) группы _________________________________________________
Теорема существования определенного интеграла
Если функция f(x) непрерывна на отрезке [ a, в ], то предел интегральной суммы существует и не зависит ни от способов разбиения на отрезке [ a, в ] на элементарные отрезки, ни от выборов точек на этих отрезках.
Если
функция f(x)
на отрезке [
a,
в ] положительна,
то определенный интеграл
![]() геометрически представляет собой
площадь криволинейной трапеции - фигуры,
ограниченной линиями
геометрически представляет собой
площадь криволинейной трапеции - фигуры,
ограниченной линиями
![]()
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
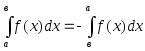 ;
2.
;
2.
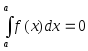 ;
3.
;
3.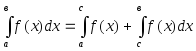 ;
;
4.
![]() ;
;
ФОРМУЛА НЬЮТОНА - ЛЕЙБНИЦА
![]() ,
где F(x)
- первообразная функции f(x)
, т.е. F(x)
= f(x).
,
где F(x)
- первообразная функции f(x)
, т.е. F(x)
= f(x).
МЕТОДЫ ВЫЧИСЛЕНИЙ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Замена переменной в интеграле
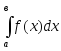 .
.
Делается подстановка х = (t) и вычисляется дифференциал dx = (t)dt. Находятся новые пределы интегрирования путем решения уравнений а = (t),
в = (t) относительно t. Тогда исходный интеграл примет вид:
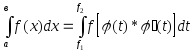 .
.
Интегрирование по частям
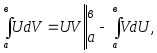
где U = U(x), V = V(x) - непрерывно дифференцируемые функции на [ а, в ].
Вычислить
определенный
интеграл:
1.
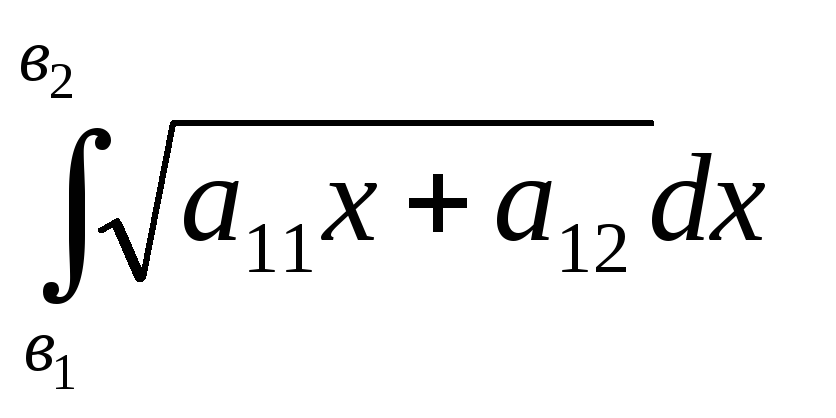 ;
2.
;
2.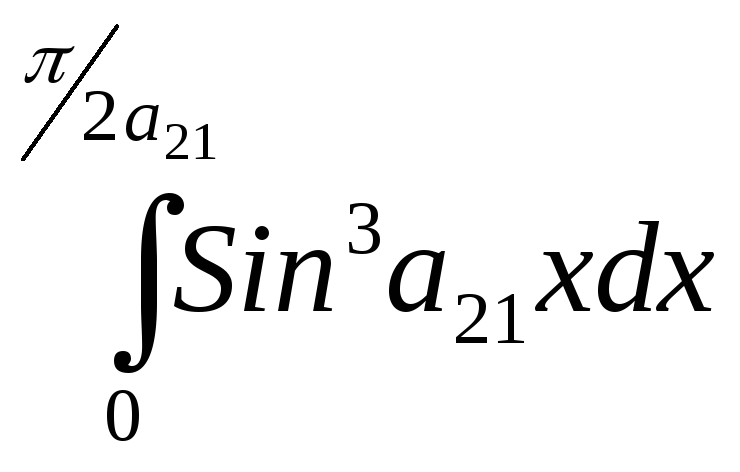 ;
;
3.![]() ;4.
;4.
![]() .
.
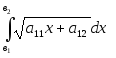 =
=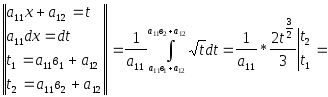
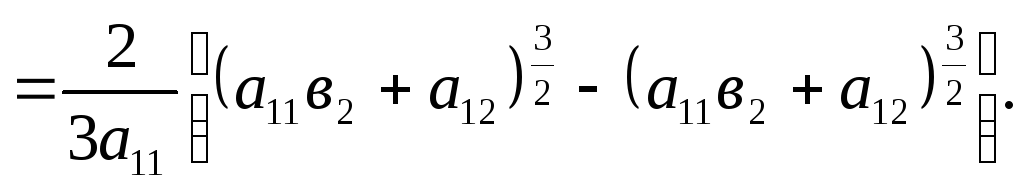
2.
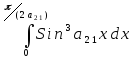 =
=
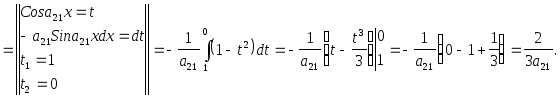
3.
![]() =
=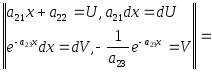
=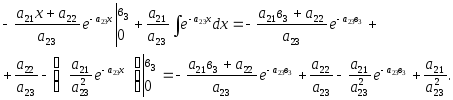
4.
![]() =
=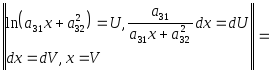
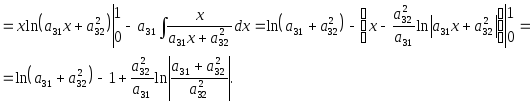
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ
Площадь криволинейной трапеции, ограниченной кривой y = f(x) [ f(x) 0 ], прямыми х = а, х = в, у = 0, вычисляется по формуле
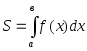 .
.

y
= f(x)












а
в
Площадь фигуры, ограниченной кривыми у = f1(x) и y = f2(x) сверху и снизу соответственно, вычисляется по формуле:
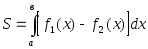 .
.
y
=f1(x)








y
= f2(x)

а
в
ПРИМЕР:
Вычислить площадь фигуры, ограниченной линиями у = -х2, х + у + 2 = 0.
Построим
график и найдем точки пересечения линий,
решив систему уравнений
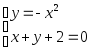 .
.
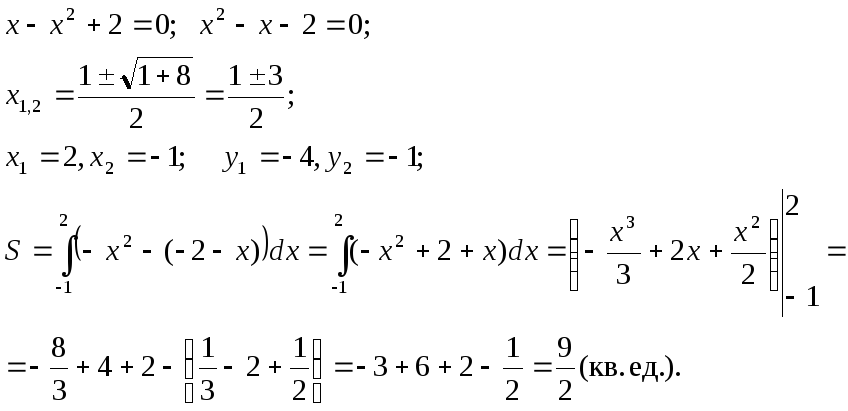
Y
2
-1
X
1


-4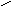
Вычисление объема тела вращения
Рассмотрим
криволинейную трапецию, ограниченную
кривой y
= f(x)
и прямыми у
= 0, х = в. Пусть
эта трапеция вращается вокруг оси Ох.
Тогда объем тела вращения вычисляется
по формуле
![]() .
.
Если
фигура, ограниченная кривыми y
= f1(x);
y
= f2(x)
(0 ≤
f1(x)
≤
f2(x))
и прямыми х
= а, х = в,
вращается вокруг оси Ох,
то объем тела вращения
![]() .
.
Рассмотрим
криволинейную трапецию
х = (у),
х = 0, у = 1, у = d.
Объем тела вращения, полученного путем
вращения этой трапеции вокруг оси Оу,
![]() .
.
Задача № 12
Найти объем тела вращения
![]()
![]()
У



Х
в





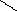
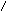
х1
в
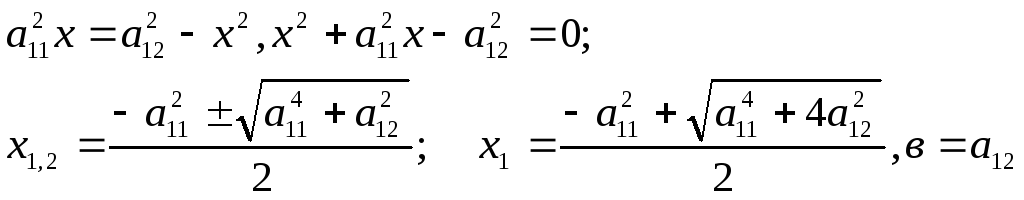
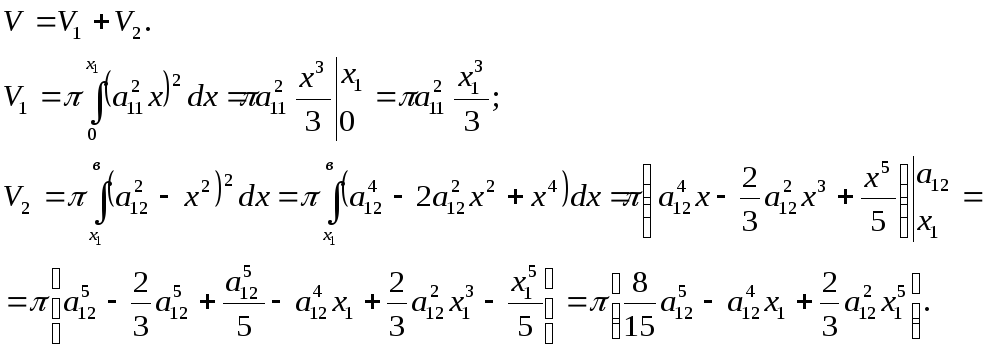
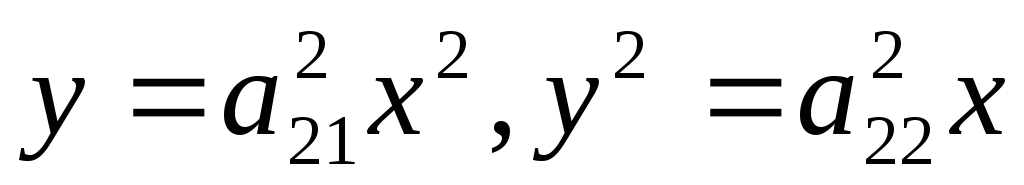 .
.
х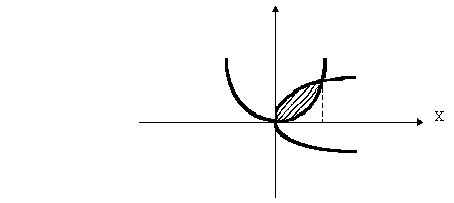

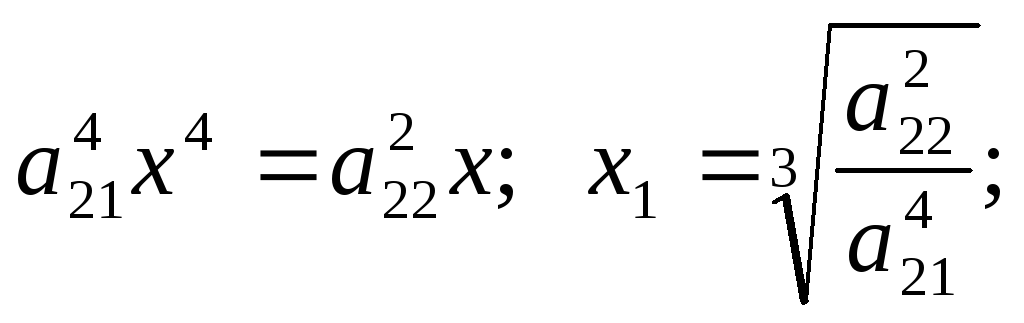

Двойной интеграл
Двойной интеграл в прямоугольных координатах
Пусть
функция
f(x,y)
определена и непрерывна в ограниченной
замкнутой области Д
плоскости хОу.
Разобьем область Д
произвольным образом на n
элементарных областей, имеющих площади
![]() S1
,
S1
,
![]() S2
, ... ,
S2
, ... ,![]() Sn
и диаметры d1,d2,
..., dn
(диаметром называется наибольшее из
расстояний между двумя точками границы
этой области). Выберем в каждой элементарной
области произвольную точку Pi(xi,
yi)
и составим следующую сумму:
Sn
и диаметры d1,d2,
..., dn
(диаметром называется наибольшее из
расстояний между двумя точками границы
этой области). Выберем в каждой элементарной
области произвольную точку Pi(xi,
yi)
и составим следующую сумму:
![]() .
.
Такая сумма называется интегральной суммой.
Определение:
Предел
интегральной суммы при условии, что
число элементарных областей
n
![]() и наибольший диаметр
max
dk
0, называется двойным
интегралом
от функции f(x,
y)
по области Д,
если этот предел существует и не зависит
:
и наибольший диаметр
max
dk
0, называется двойным
интегралом
от функции f(x,
y)
по области Д,
если этот предел существует и не зависит
:
ни от способа разбиения области Д на элементарные области;
ни от способа выбора в них точек Рi
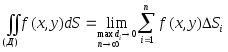 .
.
Если
f(x,
y)
0 в области
Д,
то двойной интеграл
![]() равен объему цилиндрического тела,
ограниченного сверху поверхностьюz
= f(x,
y),
сбоку - образующими параллельные оси
Оz,
а снизу - областью Д
(лежащей на
плоскости хОу).
равен объему цилиндрического тела,
ограниченного сверху поверхностьюz
= f(x,
y),
сбоку - образующими параллельные оси
Оz,
а снизу - областью Д
(лежащей на
плоскости хОу).
Свойства двойного интеграла аналогичны свойствам определенного интеграла.
