ТВиМС.Малярец.Егоршин 22.12.12

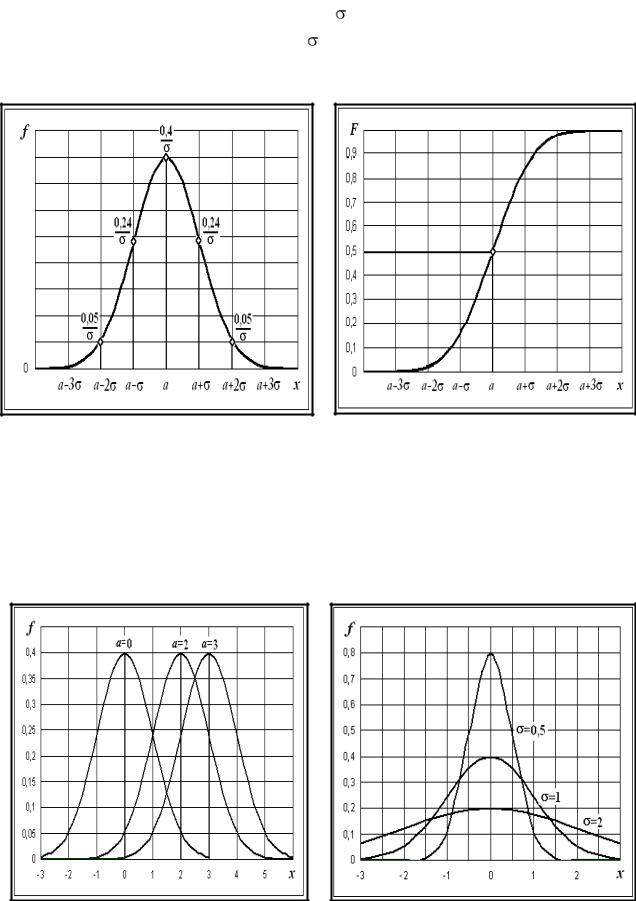
Параметры нормального закона а и х совпадают с его характеристиками: а = М(х) – математическое ожидание, х – стандартное отклонение. Коэффициенты асимметрии и эксцесса для нормального закона равны нулю.

Рис. 6.4. Графики дифференциальной и интегральной функций

нормального закона

На рис. 6.5 приведены графики плотности вероятности нормального распределения при различных значениях параметров.

Рис. 6.5. Зависимость нормального распределения от параметров

62

Для того чтобы не применять стандартную фразу: «Случайная величина х распределена нормально с характеристиками а и х», договорились использовать математическую запись x ~ N(а; х).

По аналогии с распределением Лапласа сформулируем три формы интегральной теоремы нормального закона:

1. Основная форма – вероятность попадания нормально распределенной величины х в заданный интервал с границами х1, х2:

2. Вторая форма предназначена для вычисления вероятности попадания случайной величины в интервал с симметричными границами:

Р(|x – a| t x) = 2Ф(t).

3. Утверждение, которое мы называем третьей формой интегральной теоремы нормального закона и приводим для полноты аналогии с тремя формами интегральной теоремы Лапласа, будет доказано немного позже:

x . Это не совсем правильно, но допустимо, если понимать, о чем идет речь. Ведь x – это одно число, константа, она не имеет изменчивости и потому не может быть как-то распределена. Но предполагается, что имеется n одинаково распределенных случайных величин Xi , из них составляется среднее – тоже случайная величина – Xcp= (X1 + X2 + … + Xn) / n. Утверждается, что эта случайная величина распределена нормально (центральная предельная теорема) с указанными выше характеристиками. Значения случайной величины Xcp могут быть сгенерированы (датчиком случайных чисел на компьютере) следующим образом: генерируются первые n значений случайной величины х, и из них составляется среднее – первое значение Xcp; следующие n значений х дают второе значение Xcp и т. д. Пример: вместо того, чтобы подбрасывать одновременно 10 костей и находить среднее значение выпавших очков, можно подбросить 10 раз одну и ту же игральную кость и вычислить среднее число выпавших очков за 10 бросков.

63

Найдем основные характеристики Xcp , используя свойства математического ожидания и дисперсии:

М(Xcp) = М((X1 + X2 +…+ Xn) / n) = (М(X1) + М(X2) +…+ М(Xn)) / n = = (а + а + … + а) / n = (n а) / n = а.

D(Xcp) = D((X1 + X2 + … + Xn) / n) = (D(X1) + D(X2) + … + D(Xn)) / n2 = = (Dx + Dx + … + Dx) / n2 = (n Dx) / n2 = Dx / n.

Последнее выражение в отечественной литературе называется ошибкой среднего, а в зарубежной – стандартной ошибкой.

Как и для 3-й формы интегральной теоремы Лапласа, здесь удобно пользоваться терминологией: P = 2Ф(t) – уровень доверия утверждения о том, что

грешности t nx .

В связи с этим появляются три типовых задачи.

I. Известны параметры распределения а и х. Дополнительно заданы n и погрешность . Найти уровень доверия Р.

II. Известны параметры распределения а и х. Дополнительно заданы n и уровень доверия Р. Найти погрешность .

Решение. Из P = 2Ф(t) по таблицам Лапласа находим t. Далее вычисляем

При изучении 3-й формы интегральной теоремы Лапласа была рассмотрена еще одна задача (IV), которая формулируется так: «Известны результаты опыта. Что можно сказать о теоретических характеристиках распределения?»

64

Подобные задачи составляют предмет математической статистики и будут рассмотрены в соответствующих разделах курса.

Показательный, или экспоненциальный, закон распределения

По этому закону распределено время работы оборудования до первого отказа. Его дифференциальная функция с точностью до постоянного сомножителя выражается формулой: f(t) = ke– t – для t 0; для t < 0 f(t) = 0.

Сомножитель k находим из условия – площадь под дифференциальной кривой равна единице:

вания по частям; внеинтегральный член оказался равным нулю. Математическое ожидание – это среднее значение случайной величины,

центр тяжести фигуры под дифференциальной кривой.

Для вычисления дисперсии предварительно найдем M(t2):

Тогда

Наивероятнейшее значение (мода) для показательного распределения равно нулю, то есть Мо = 0 (чаще всего оборудование выходит из строя в момент включения).

65

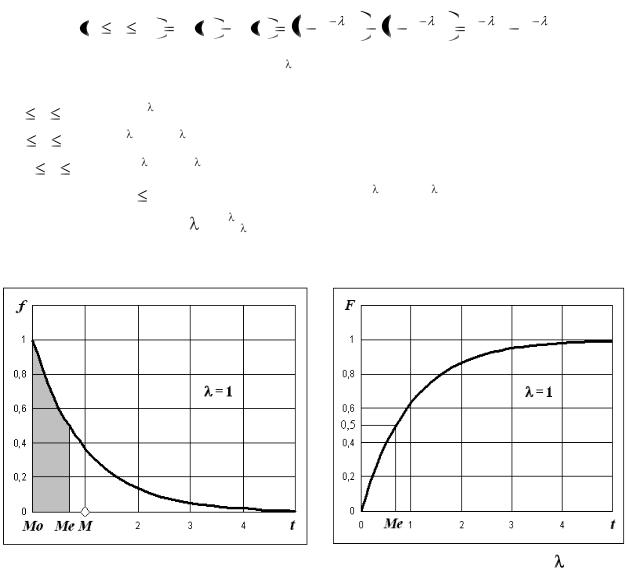
Интегральная теорема для показательного закона выглядит так:

Рис. 6.6. Функции распределения показательного закона для = 1

Квантили распределения

Для непрерывной случайной величины в качестве дополнительных характеристик используют так называемые квантили, к которым относятся медиана, квартили, децили и процентили.

Квантили делят фигуру под дифференциальной кривой на равновеликие части, или же они делят интервал изменения (варьирования) случайной величины на равновероятные части.

Медиана делит интервал варьирования на две части с вероятностью 50 % попадания случайной величины в каждую часть.

Квартили делят интервал варьирования на четыре части с вероятностью 25 % попадания случайной величины в каждую часть.

Децили делят интервал варьирования на десять частей с вероятностью 10 % попадания случайной величины в каждую часть.

66

Множитель А находим из условия равенства единице площади под диф-

Вычисляем дисперсию отклонений (при этом учтем, что М(х) = 0):

Этот интеграл вычисляется по правилу «интегрирования по частям». Окончательно получаем:

то есть отклонения попаданий от точки прицеливания действительно распределены нормально.

Вопросы для самопроверки

1.Что такое функция распределения? Каковы ее свойства и график? Как она называется для дискретной случайной величины?

2.Сформулируйте общую интегральную теорему, приведите ее вариант для непрерывной случайной величины.

3.Что такое функция плотности вероятности, каковы ее свойства и

график?

4.Как связаны между собой функция распределения и функция плотности вероятности?

5.Как вычисляются основные характеристики непрерывной случайной величины?

6.Сформулируйте закон равномерного распределения, опишите область его применения, приведите выражения для дифференциальной и интегральной функций.

7.Опишите характеристики равномерного закона. Выполняется ли для него правило «3-х сигм»?

8.Сформулируйте показательный закон распределения, опишите область его применения, приведите выражения для дифференциальной и интегральной функций. Опишите характеристики показательного закона.

68

9. Что такое нормальный закон распределения Гаусса, каковы его характерные особенности?

10. Какие отличия имеются между нормальным распределением и распределением Лапласа?

11. Каковы параметры и характеристики нормального закона?

12. Сформулируйте три формы интегральной теоремы нормального закона.

13. Какие задачи решаются с помощью 3-й формы интегральной теоремы нормального закона?

14. Что такое квантили? Перечислите их разновидности. 15. Что такое медиана и как она рассчитывается?

16. Что такое квартили и как они рассчитываются?

7.Предельные теоремы теории вероятностей

Кпредельным теоремам теории вероятностей относят закон больших чи-

сел и центральную предельную теорему. Строго говоря, предельными явля-

ются также асимптотические формулы Пуассона и Лапласа, но они формально не относятся к упомянутому выше разделу теории вероятностей.

В доказательстве закона больших чисел и центральной предельной теоремы принимали участие русские математики Чебышев П. Л. и Ляпунов А. М., и, может быть, поэтому в отечественной научной литературе доказанным теоремам придается слишком большое, чуть ли не мистическое, значение. В действительности же доказывались очевидные вещи, в справедливости которых никто не сомневался. Здесь имеет место принцип: математики всегда доказывают все утверждения в отличие от представителей инженерных наук, которые никогда не доказывают утверждения, в справедливости которых уже убедились на основе опытов или правдоподобных рассуждений.

Закон больших чисел

1. Теорема Бернулли. Доказывается, что при увеличении числа однородных независимых испытаний относительная частота появления события A стремится к ее вероятности.

Это предположение изначально лежит в основе универсального метода статистического определения вероятностей:

69

Для строгого доказательства рассмотрим 3-ю форму интегральной теоремы Лапласа:

При t = 3 уровень доверия (вероятность выполнения этого условия, гарантия) уже равен Р = 0,997. Если потребуется еще больший уровень доверия, можно принять t = 4, 5 и даже 10. Таким образом, с гарантией, сколь угодно близкой к единице, можно утверждать, что отклонение относительной часто-

2. Теорема Чебышева. Доказывается, что с увеличением повторных измерений среднее значение величины приближается к своему математическому ожиданию.

В справедливости этого утверждения также никто не сомневался. Действительно, пусть случайная вели-

значения xi , где (m1 + m2 + m3 + … mk)= n. Тогда среднее значение случайной величины по этим n наблюдениям будет равно:

Для строгого доказательства рассмотрим неравенство Чебышева, которое ранее использовали для обоснования правила «3-х сигм», но сейчас запишем это неравенство для случайного среднего Xcp :

При t = 10 гарантия этого утверждения будет больше 0,99; если требуется еще больший уровень доверия, принимаем еще большее значение t.

Таким образом, с гарантией, сколь угодно близкой к единице, можно утверждать, что отклонение среднего от математического ожидания не превысит погрешности, которая стремится к нулю при увеличении n:

70