33.Теорема о размерности ядра и образа ло.

Пусть А:RⁿRⁿ

Тогда dim (Ker A)+dim (ImA)=n

Замечание: dim (ImA)=rangA, dim(Ker A)=defA – дефект Л.О

Пусть (e₁, e₂, … e_n)=e базис в Rⁿ и A –матрица Л.О А

KerA = {xRn: Ax=} Ax(e)== - ЛОС

dim (kerA) - Число линейных независимых решений ЛОС = n-r, т.е. dim(kerA) = n-r => n=dim(kerA) + r и т.к. к=rangA=rangA, имеем, n=rangA+dim(KerA)

№34 Действия над ЛО. Обратный оператор. Теорема об обратном операторе.

Действия над ЛО:

Пусть A, B: RⁿRⁿ, VV

1)A=B, если Ax=Bx, xRⁿ (равенство ЛО)

2)A+B=C: (A+B)(x)=Ax+Bx, xRⁿ (сумма ЛО)

3)A=C: (R): (A)(x)=(Ax), xRⁿ (произведение ЛО на число)

4)A*B=C: (AB)(x)=A(Bx), xRⁿ (произведение ЛО)

5)ЛО A^-1 называется обратным к ЛО А, если A*A^-1=A^-1*A=I (Ix=x – тождество ЛО)

Теорема об обратном операторе:

Пусть ЛО A: RⁿRⁿ, тогда равносильны утверждения:

1)A^-1

2)A – взаимооднозначен

Замечание:

ЛО А называется взаимооднозначным, если из Ax=Ay x=y; x, yRⁿ

3)KerA={}

4)rangA=n

Доказательство:

12

Пусть A^-1 и Ax=Ay A^-1(Ax)= A^-1(Ay) (A^-1A)x=(A^-1A)y Ix=Iy x=y A – взаимооднозначен

23

Пусть A – взаимооднозначен и Ax=0=A* x= KerA={}

34

KerA={} dim(KerA)=defA=0, а т.к. defA+rangA=n, rangA=n

41

rangA=n и (l₁…l_n)=l – базис в Rⁿ g_k=Al_k: (g₁…g_k)ImA – базис в R^k

Пусть В – ЛО, переводящий g_k в l_k Bg_k=l_k и Al_k=g_k

(B*A)(x)=B(Ax)=B(A())=B()===x B*A=I(аналогично A*B=I) B=A^-1

№35 Теорема о ранге произведения ЛО.

Пусть A, B: RⁿRⁿ, тогда:

1)rang(AB)min(rangA, rangB)

2)если rangA=n, то rang(AB)=rangB

3)если rangB=n, то rang(AB)=rangA

Доказательство:

1)W₂W₁ dimW₂=rang(AB) dimW₁=rangB, т.к. W₁Rⁿ, то W₂ImA dimW₂=rang(AB)dim(ImA)=rangA

2)пусть rangA=n ImA=Rⁿ ImB=Im(AB) rangB=rang(AB)

3)аналогично

Следствие:

Пусть A, BP_n², тогда:

1)rang(AB)min(rangA, rangB)

2)если detA0, rang(AB)=rangB,

detB0, rang(AB)=rangA

№36 Собственные числа (СЧ) и собственные вектора (СВ) ЛО.

Характеристическое уравнение.

Свойства СЧ и СВ ЛО.

Вектор g называется собственным вектором ЛО А, если R; Ag=g

 - собственное число А, g

g=Ig, пусть A– матрица ЛО A в базисе l=(l₁…l_n)

Ag=g ~ Ag(l)=g ~ (A - I)g==,

ЛОС имеет ненулевое решение: det(A-I)=0

det(A-I)=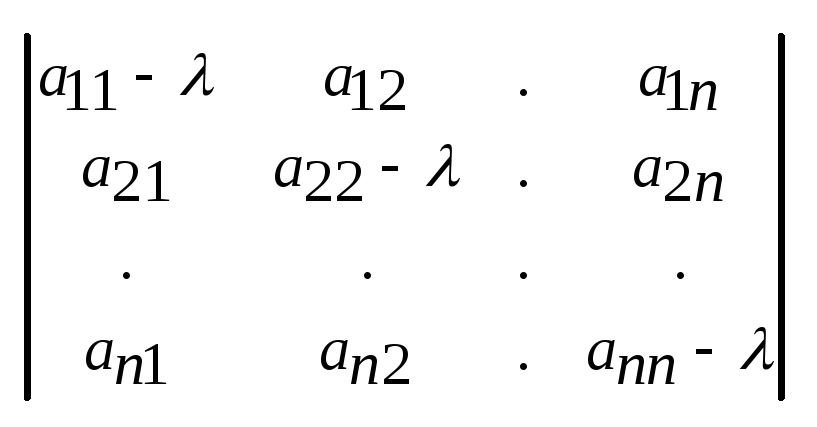=(-1)ⁿⁿ+(-1)^n-1(a₁₁+…a_nn)^n-1+…+detA=0 – характеристическое уравнение.

Свойства СЧ и СВ ЛО А:

1)число СЧn

2)₁…_m – СЧ

g₁…g_m – СВ, соответствующие СЧ

если _i_j, то g₁…g_m – линейно независимы

3)M_ - множество СВ, соответствующих СЧ , тогда { M_, }=W_ - ЛПП

4)если  - корень характеристического уравнения кратности S, то dimW_S

5)если для ЛО А n различных СЧ, то соответствующие СВ образуют базис в Rⁿ и матрица А – диагональна в этом базисе

Доказательство:

1)следует из основной теоремы алгебры

2)докажем по индукции:

а)m=1 – очевидно

б)(m-1) СВ линейно независимы

A(₁g₁+…+_mg_m)=, тогда в силу линейности оператора

A(₁g₁+…+_mg_m)=₁₁g₁+…+_m-1_m-1g_m-1+_m_mg_m= (1)

₁_mg₁+…+_m-1_mg_m-1+_m_mg_m= (2)

Вычтем из (1) (2):

₁(₁-_m)g₁+…+_m-1(_m-1-_m)g_m-1=

Т.к. g₁…g_m-1 – линейно независимы, то

_k(_k-_m)=0 (k=1, m-1), причем (_k-_m)0

Значит, _k=0 _m=0 g₁…g_m – линейно независимы.

3)Пусть g₁, g₂ – СВ для  ₁g₁+₂g₂ – СВ. Действительно, А(₁g₁+₂g₂)= А₁g₁+А₂g₂= ₁g₁+₂g₂= (₁g₁+₂g₂)

W_={M_, } – ЛПП

4)Пример:

4.1)- хар.ур.

(-3)²=0

=3 – корень кратности 2

Решаем уравнение:

(A-I)g=

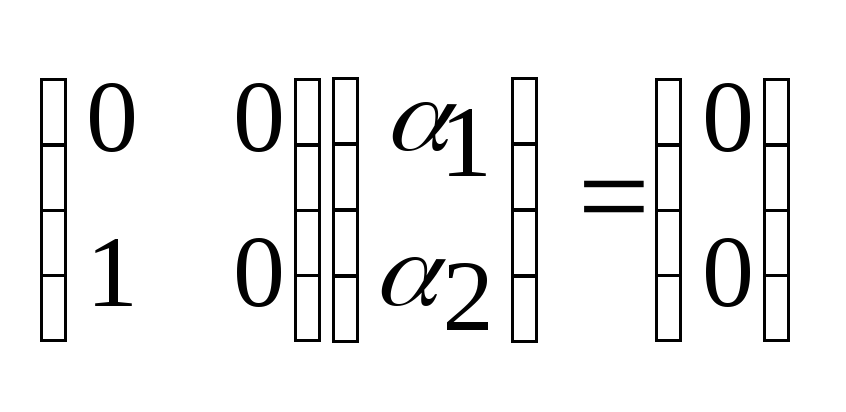
n=2 rangA=1

, значит, dimW₃=1<2

4.2)

=3 – корень кратности 2

rangA=0 Значит, любой вектор – решение

dimW₃=2=2

5)Пусть ₁…_n – СЧ,

g₁…g_n – СВ

_i_j g₁…g_n – линейно независимы по свойству 2 это базис в Rⁿ

Ag₁=₁g₁

…

Ag_n=_ng_n

Замечание:

Матрицы A и В называются подобными, если существует матрица SP_n, (|S|0): B=SAS^-1

Если ЛО А имеет n различных СЧ, то матрица А подобно-диагональна

№37 Самосопряжённый оператор, критерий самосопряжённости.

Пусть А: EⁿEⁿ

ЛО А* называется сопряжённым к А, если x, yEⁿ: (Ax, y)=(x, A^*y); если А=А^*, то А называется самосопряжённым ЛО ((Ax, y)=(x, Ay))

Теорема: (критерий самосопряжённости)

А: EⁿEⁿ

А является самосопряжённым (СЛО)матрица А симметрична в ОНБ

Доказательство:

Пусть (e₁…e_n)=E – ОНБ и А – СЛО,

=

a_ij=a_ji A=A^T т.е. матрица симметрична.

Пусть А – матрица ЛО А в ОНБ e и a_ij=a_ji

,

(Ax, y)=(A(),)=

(x, Ay)=( , A())=

но a_ij = a_ji Значит, (Ax, y)=(x, Ay)

№38 Свойства СЧ и СВ самосопряжённого оператора.

1)если ₁, ₂ – СЧ,

g₁, g₂ – СВ, тогда, если ₁₂, то g₁ и g₂ – ортогональные

2)СЧ СЛО действительны

3)если _ - корень хар.ур. кратности S, то dimW_=S

4)B Eⁿ ОНБ из CВ СЛО

Доказательство:

1) ₁, _n – СЧ ₁₂

(Ag₁,g₂)=₁(g₁,g₂)

(Ag₁,g₂) = (g₁,Ag₂)=₂(g₁,g₂)  (₁-₂)(g₁,g₂)=0  (g₁,g₂)=0 => g₁  g₂

2)Пусть А – матрица СЛО А, то А=А^т

=+i - СЧ

=-i - СЧ

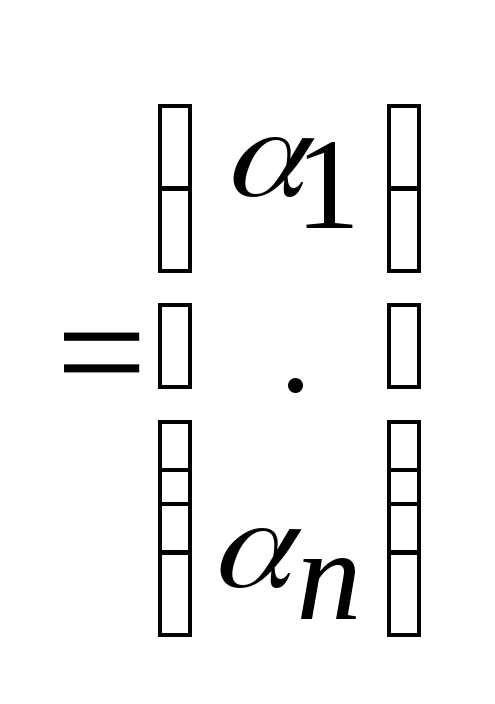kk

Действительно: Ak=k

Ak=A*k=k=*k

Заметим: k^тk=₁₁+…+_n_n=|₁²|+…+|_n²|=²>0

k^тAk= k^тk=²

k^тAk = (k^тAk)^т=k^тА^тk=k^тAk=k^тk=²

(-)²=0 = R

4)₁ – корень кратности S_i, тогда

dimW_1=S₁  ОНБ e₁¹…e_S1¹

_m – корень кратности S_m dimW_m=S_m  ОНБ e₁^m…e_Sm^m

Т.к. СЧ  R, то ₁+…+_m=n  e₁¹…e_S1¹… e₁^m…e_Sm^m – ОНБ в Rⁿ

№39 Ортогональные операторы, свойства, ортогональная матрица.

ЛО : EⁿEⁿ называется ортогональным, если x, yEⁿ: (x, y)=(x, y)

Свойства:

1)ОЛО сохраняет длины векторов и углы между ними

2)

3)если , то А – ОЛО

4)еслт Р – матрица ОЛО в ОНБ, то Р^тР=I (Р^т=Р^-1)

Доказательство:

1)из определения

2)из 1

3)Пусть e=(e₁…e_n) – ОНБ

e_k’ – образ e_k

e_k’=A e_k (k=1,n)

(e₁’… e_n’)= e’ – ОНБ

,

(x, y)=

(Ax,Ay)=(A(), A())=(Ae_i, Ae_j)= e_i’*e_j’= = (x, y)

4)P – матрица ОЛО в ОНБ

коор

Ae₁

(Pe_i, Pe_j)= ()()= =

=

A, BP_n²

A*B=

A^т*B=

P^т*P=

P^тP=I, т.е. P^-1=P^т – ортогональная матрица

40. Пусть V – ЛП над P. Опр. Функция называется линейной формой (ЛФ) если.Вид ЛФ в конечномерном ЛП: - базис вV; ; (₁… _n)^T=x(e); ; .

Опр. Функция называется билинейной формой (БФ), если для.

БФ называется симметричной если (x,y)=(y,x). Если БФ симметричная, то .Вид БФ в конечномерном ЛП: - базис вV; ;;(e_i,e_j)=a_ij; 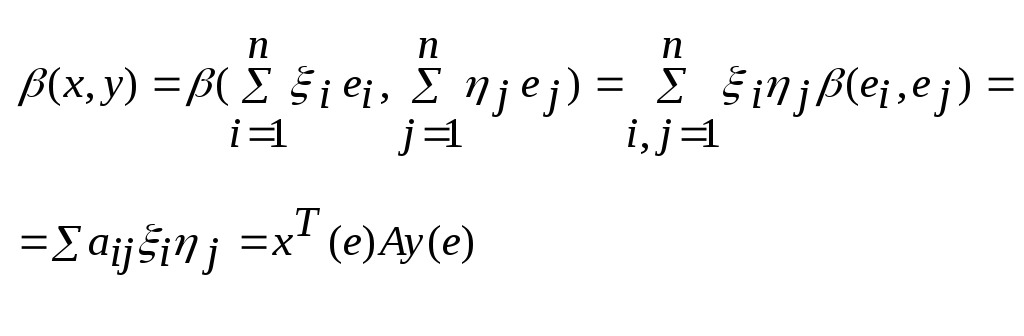;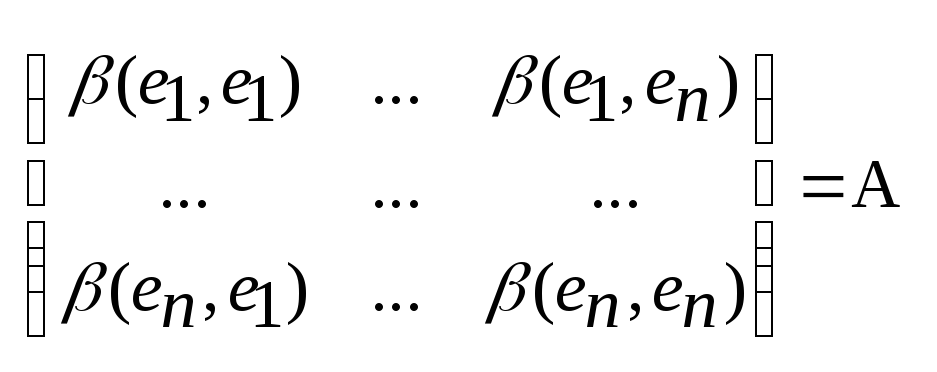- матрица БФ.

Опр. Пусть (x,y) – симметричная БФ. Функция вида k(x)=(x,x) называют квадратичной формой (КФ). (x,x) называют полярной БФ к k(x). Вид КФ в конечномерном ЛП: ; А – матрица КФ.

Классификация КФ. 1) КФ k(x) называется положительно (отрицательно) определенной если для ; 2) КФk(x) называется знакопеременной если ; 3) КФk(x) называется квазизнакоположительной (отрицательной) если k(x)0 (k(x)0) и yV (y): k(y)=0

41. - канонический вид КФ, где_i – канонические коэффициенты.

Приведение КФ к каноническому виду ортогональным преобразованием.

Еⁿ – вещественное евклидово пространство; k(x) – КФ. Опр. Линейный оператор называется присоединенным кk(x) если : 1) А – самосопряженный ЛО; 2) k(x)=(Ax,x).

Теорема (о присоединенном ЛО): пусть в Еⁿ задана КФ k(x), тогда : 1)  присоединенный ЛО А ((Ax,x)=k(x)) ; 2) в любом ОНБ матрица ЛО A совпадает с матрицей k(x).

Теорема (о приведении КФ к главным осям): пусть в ОНБ (е₁…е_n) КФ , тогда ОНБ из СВ присоединенного ЛО А в котором КФ, где_I – СЧ А. Док-во. По предыдущей теореме  присоединенный ЛО А к КФ k(x) и . Пусть- ОНБ из СВ А и, тогда

42. Метод Лагранжа (выделение полного квадрата). 1) а₁₁0; 2)а_ii=0 ; , где₁=₁+₂, ₂=₁-₂, ₃=₃, ..

Метод Якоби. 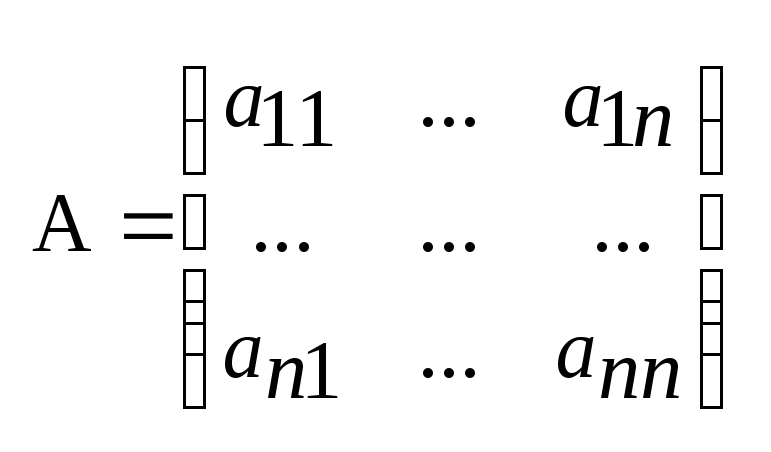- матрица КФk(x); - главные миноры.

Теорема Якоби: пусть главные миноры матрицы КФ _k0, тогда  базис в котором , где_k=_k/_k-1 (₀=1)

43. Опр. Ранг КФ k(x) (r(k)) – число равное рангу матрицы КФ в некотором базисе. (Если , тоr(k) – число ненулевых канонических коэффициентов).

Теорема (закон инерции квадратичных форм): число положительных (отрицательных) канонических коэффициентов КФ не зависит от выбора канонического базиса. Док-во. Пусть - в базисеи- в базисе(a,b,c,d>0) ; 1) r(k)=l=m; 2) допустим, что p<q. Рассмотрим W₁=Z(f₁…f_q), dim W₁=q и W₂=Z(e_p+1…e_n), dim W₂=n-p; dim(W₁+W₂)n; dim(W₁+W₂)=dim W₁ + dim W₂ – dim(W₁W₂)  dim(W₁W₂)= dim W₁ + dim W₂ - dim(W₁+W₂)  q+n–p–n=q–p>0  ( x₀  0): x₀W₁W₂  x₀W₁, x₀W₂  иполучили противоречие pq аналогично можно доказать что pq  p=q.

Опр. Положительный (отрицательный) индекс КФ i₊(i _-) положительных (отрицательных) канонических коэффициентов (i₊=p, i _-=m-p, r(k)=m).

Теорема (о классификации КФ): пусть в Еⁿ задана КФ k(x), тогда: 1)КФ – положительна (отрицательно) определена  i₊=n (i _-=n); 2) КФ – знакопеременная  i₊>0, i _->0; 3) КФ = квазиположительная (отрицательная)  0<i₊<n, i _-=0 (0<i _-<n, i₊=0). Док-во. 1) «»i₊=n  приx0  КФ – положительнопределена. «» КФ – положительно определена и i₊<n, и пусть в каноническом базисе i₊=k<n  k(x₀)0 и x₀0 пришли к противоречию.

44. Теорема (критерий Сильвестра): пусть в Еⁿ задана КФ и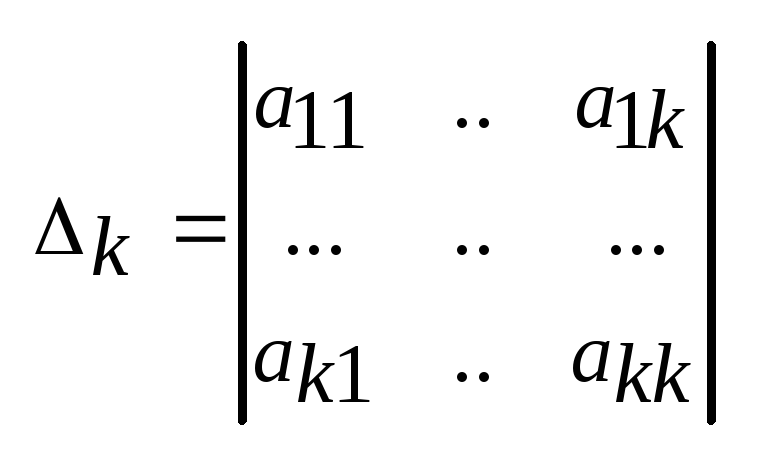- главные миноры матрицы А, тогдаk(x) положительно (отрицательно) определена  _k>0, k=1,n ((-1)^k_k>0, k=1,n). Док-во. «» КФ – положительно определена  _k0. Докажем от противного: пусть _m=0 - ЛОС. Так как_m=0, то ЛОС имеет не нулевое решение . Возьмем, тогда- противоречие _m0. По теореме Якоби  ОНБ в котором (_k>0)  ₁=₁>0; ₂=₂/₁>0₂>0;…; _n=_n/_n-1>0 _m>0.

«»_k>0 по теореме Якоби ₁=₁>0, ₂=₂/₁>0,…, _n=_n/_n-1>0 i₊=n  k(x) – положительно определена.

КФ отрицательно определена. Пусть k(x) – отрицательно определена  -

положительно определена   (-1)^k_k>0  ; (,).

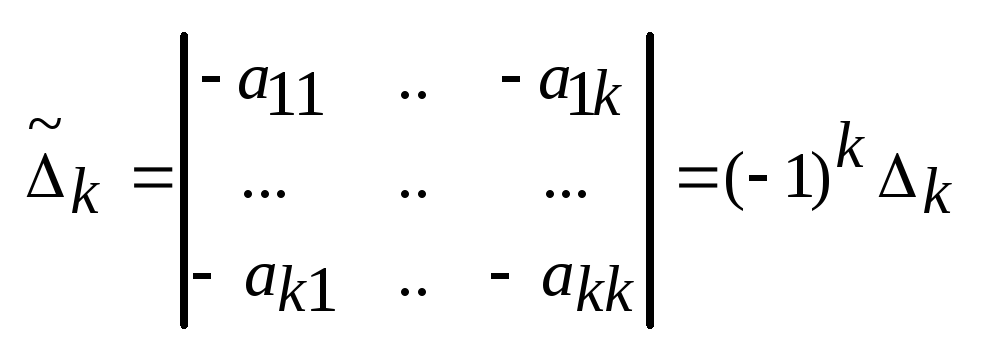45. Теорема (о приведении 2-х КФ к каноническому виду): пусть и- в базисе, еслиk₁(x) положительно определена, то  ОНБ в котором k₁(x) и k₂(x) имеют канонический вид. Док-во. Пусть k₁(x) положительно определена   ОНБ в котором. Пусть, тогда ОНБ из СВ матрицыB_f в котором , где_k – СЧ матрицы B_f. Пусть S - матрица перехода от базиса f к базису g  S - ортогональная матрица  , гдеA_g=S^-1I S  . Т.о. нашли базис в котором две КФ имеют канонический вид.