7. Разложение определителя по строке ( столбцу ).

Опр: AP_n^2. Опр-ль матрицы, полученной из матр А путем вычеркивания i-той строки и j-того столбца наз-ся минором к элементу, леж-му на пер-ии вычеркнутых строки и столбца. M_ij – минор. (-1)^i+jM_ij = A_ij – алг.дополнение к a_ij. Лемма: Пусть тогда detA = a_ijA_ij Док-во: 1)i=j=n, имеем ; detA==a_nn=a_nnA_nn 2) Общий случай: С помощью (n-i) соседних перестановок строк и (n-j) соседних перестановок столбцов сделаем a_ij  a_nn; Тогда detA = (-1)^n-i+n-ja_ijM_ij=a_ijA_ij Трм: Пусть AP_n^2. Тогда detA=Док-во: |A| = = (по лемме) = ++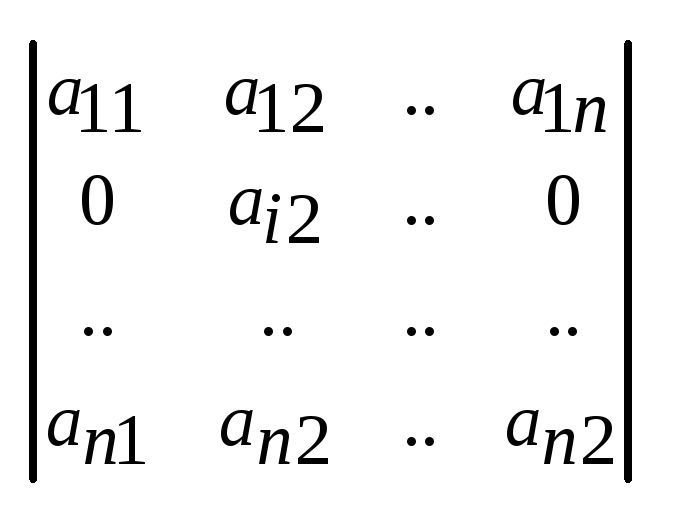...+= a_i1A_i1+ a_i2A_i2+... +a_inA_in =

8.Теорема Лапласа о разложении определителя по m строкам (без док - ва). Пример.

Опр: AP_n^2. Опр-ль матрицы из элементов, расположенных на пересечении k выделенных строк и столбцов – минор k-того порядка. (m^i1...ik_j1...jk) Определитель матрицы, сост-й из эл-тов, оставшихся после вычеркивания – дополнительный минор k-того порядка. (M^i1...ik_j1...jk); A ^i1...ik_j1...jk = (-1)^{i1+...+ik+j1+...+jk} *M^i1...ik_j1...jk

Трм. Пусть в AP_n^2. выделено k строк (i₁...i_k) Тогда detA = ∑[m^i1...ik_j1...jk*A ^i1...ik_j1...jk], суммирование по всем выборкам j₁...j_k;

Прим1: H = = где A, B, C, 0 P_n^2; HP_(2n)^2 ; detH = detAdetC(-1)^2*(1+2+..+n) = |A|*|C|; Прим2: H = detH = detBdetC(-1)^{2*(1+2+..+n + (n+1)+..+2n)} = |B|*|C|(-1)^{2n(2n+1) \ 2} = |B|*|C|(-1)ⁿ

9.Теорема об определителе произведения матриц.

A,BP_n^2. Тогда det(AB)=detA*detB; Д-во: С=AB; E – единичная матрица. detD == = т.Лапласа = detA*detB = (непонятно_как

к 1-ой строке прибавляем (n+1)a₁₁+(n+2)a₁₂+...+(2n)a_1n

ко 2-ой строке прибавляем (n+1)a₂₁+(n+2)a₂₂+...+(2n)a_2n

....

к n-ой строке прибавляем (n+1)a_n1+(n+2)a_n2+...+(2n)a_nn) = == (-1)ⁿdetE detC = (-1)²ⁿdetC = detC, чтд.

16. Метод Гаусса решения ЛС.,AP_mn, rang(A)=k

Запишем матрицу системы:

,

ЛС – совместимая.

17. Однородные системы линейных уравнений ( ЛОС ), свойства решений ЛОС.- ЛОС,AP_mn

Свойства: 1. не бывает несовместных ЛОС (); 2. если α₁, … α_k – решение ЛОС, тогда - решение ЛОС (сR); 3. ЛОС определена  rang(A)=n; 4. пусть AP_nn, тогда для того, чтобы ЛОС имела единственное решение det(A)=0

Док-во: 2. пусть α₁, α₂ – решения и с₁,с₂R - решение. По индукции можно провести доказательство для n корней

3. пусть rang(A)=n  и- линейно независимые - ЛОС; с₁=с₂=…=с_n=0, это значит, что ЛОС имеет решение

18. Фундаментальная система решений ЛОС ( ФСР ). Теорема о существовании ФСР. Структура общего решения ЛОС. Фундаментальной системой решений (ФСР) ЛОС называется набор решений, такие что 1.- линейно независимы; 2. (- решение ЛОС)(с₁,…с_кR):

Теорема о существовании ФСР ЛОС:

Пусть AP_mn – матрица ЛОС иrang(A)=k (k<n). Тогда существует ФСР из (n-k)

Док-во: Пусть - базисный минор., гдеx₁,…,x_k – базисные переменные, а x_k+1,…,x_n – свободные параметры.

Положим x_k+1=1, а остальные x_k+2=…=x_n=0  x₁=c₁₁…x_k=c_1k, затем

x_k+2=1, x_k+1= x_k+3=…=x_n=0  x₁=c₂₁…x_k=c_2k

x_n=1, x_k+1= x_k+2=…=x_n-1=0 x₁=c_n-k1…x_k=c_n-kk

…

Проверка:

1. ,M_n-k0  rang(B)=n-k  - линейно независима

2. Пусть - решение ЛОС;- решение ЛОС

- решение ЛОС

, т.к. M_k0  y_i-d_i = 0, 

Следствие: множество решений ЛОС называется общим решением, где_iR, - ФСРЛОС

19. Неоднородные линейные системы ( ЛНС ). Структура общего решения ЛНС.- ЛНС,AP_mn (m – число уравнений, n – число неизвестных); - приведённая однородная система (ПОС)

Свойства решений ЛНС:

1. - решение ЛНС, - решение ПОС - решение ЛНС

2. , - решение ЛНС- решение ПОС

3. Пусть - решение ЛНС, тогда для любого решения ЛНС -:- решение ПОС

Доказательство:

1. 

2. 

3. Пусть - решение ЛНС - решение ПОС

Множество всех решений ЛНС называется общим решением

20. Аксиоматика линейного пространства ( ЛП ), примеры, свойства ЛП. Множество V называется линейным пространством (ЛП) над полем Р, если в V заданы 2 операции:

4. x + y  V – операция сложения элементов этого множества

5. α  x  V, хV, αP – умножение на число

удовлетворяющие условиям:

1. x + (y + z) = (x + y) + z – ассоциативность

2. : x +  =  + x = x – существование нулевого вектора

3. хV, (-x): x + (-x) =  - существование противоположного вектора

4. x + y = y + x - коммутативность

5. 1  x = x – свойство единичного элемента

6. (  ) x =  ( x) – ассоциативность относительно умножения

7.  (x + y) =  x +  y – дистрибутивность относительно векторов

8. ( + ) x =  x +  x – дистрибутивность относительно чисел

1) – 4) – абелева группа

Свойства операций:

1. Единственность . Доказательство: Пусть ₁ и ₂ – два нулевых элемента в V, тогда ₁ = ₁ + ₂ = ₂

2. Единственность (-x). Доказательство: (-x₁) и (-x₂) – противоположны к х, тогда (-x₁) + х + (-x₂) = (-x₁) +  = (-x₂) +  = -x₁ = -x₂

3. 0  x = . Доказательство:   x = ( + 0) х =   x + 0  х =   x +  =   x

4. – х = (-1) х. Доказательство: 0  х = (1 + (-1)) х = 1 х + (-1) х = х + (-1) х, то есть – х = (-1) х

5.    = . Доказательство:    =  (х – х) =  (1 х + (-1) х) =  (1 + (-1)) х =   

6.  х =    = 0 или х = . Доказательство: 1. Пусть   0, . 2. Пусть = 0  0  x = 

7. Вычитание векторов: разность векторов (x – y) – вектор z, z + y = x, z = x + (-y)

8. ( - ) x =  x -  x

Примеры ЛП:

1. V = P_mn

2. V = Rⁿ

3. V = C_[a;b]

4. V – множество решений ЛОС

5. V = Р_n – множество многочленов степени n

если P = R, то V – вещественные ЛП; P = С, то V – комплексные ЛП

21. Подпространства, свойства. Сумма и пересечение подпространств. Линейная оболочка множества векторов. Множество WV называется линейным подпространством (ЛПП) ЛП V, если оно замкнуто относительно сложения векторов и умножения вектора на число. Т.е. x, y  W: x + yW; xW и R:  xW

Пересечение ЛПП W₁ и W₂: W₁W₂ = {х | xW₁, xW₂}

Сумма ЛПП W₁ и W₂: W₁+W₂ = {х | х = х₁ + х₂, x₁W₁, x₂W₂}

Свойства ЛПП: Пусть W₁, W₂V – ЛПП

1. W₁, W₂ – ЛП. Доказательство: W₁, Пусть хW₁  0  х = W₁

2. W₁W₂ – ЛПП. Доказательство: W= W₁W₂. Пусть x,yW  x,yW₁, x,yW₂  x+yW₁, x+yW₂  x+y W₁W₂= W. Аналогично  х

3. W₁+W₂ – ЛПП.

4. Пусть даны два вектора a₁ и a₂ (не параллельны). Введём

W₁={x=*a₁} и W₂={x=βa₂}. Тогда W₁+W₂={x=*a₁+ βa₂}