
- •1.Сложение матриц. Умножение матрицы на число. Свойства операций.
- •2. Произведение матриц. Свойства произведения.
- •3.Перестановки, инверсии и транспозиции.
- •4.Теорема о транспозиции. Четность перестановки.
- •6. Определитель n- го порядка: определение и свойства.
- •7. Разложение определителя по строке ( столбцу ).
- •8.Теорема Лапласа о разложении определителя по m строкам (без док - ва). Пример.
- •9.Теорема об определителе произведения матриц.
- •22. Линейная зависимость (лз) векторов в лп, свойства. Основная трм о лз.
- •23.Базис и координаты в лп, свойства, примеры. Размерность лп.
- •24. Замена базиса. Формулы перехода.
- •25. Изоморфизм лп. Теорема об изоморфизме.
- •26. Прямая сумма и прямое дополнение. Теорема о прямом дополнении. Теорема о размерности суммы подпространств.
- •27.Cкалярное произв-е векторов: определение и св-ва. Евклидово пространство, примеры.
- •33.Теорема о размерности ядра и образа ло.
25. Изоморфизм лп. Теорема об изоморфизме.
Пусть V, V' над P. V и
V’
называют изоморфными (V=~V’)
если сущ-т взаимнооднозначное соответствие
(изоморфизм) φ:V
-> V’
такое, что 1) φ(x,y) = φ(x)
+ φ(y),
для
![]() x,y
x,y
![]() V. 2) φ(αx)
= αφ(x),
V. 2) φ(αx)
= αφ(x),
![]() x
x
![]() V,
V,
![]() α
α![]() R.
(NB:
Если φ – изом-м, то φ(Θ) = Θ', Θ
R.
(NB:
Если φ – изом-м, то φ(Θ) = Θ', Θ![]() V,
Θ ‘
V,
Θ ‘![]() V’.
φ(Θ)= φ(0x)=0*
φ(x)=
Θ’.
V’.
φ(Θ)= φ(0x)=0*
φ(x)=
Θ’.
Трм Пусть
V, V' – конечномерные ЛП над P. Тогда V=~V’
необх\дост dimV=dimV' (т.е. все конечномерные
ЛП одной размерности изоморфны). Док-во:
Дость: пусть
dimV=dimV' и пусть e1..en
= E
– базис в V,
E’
= e’1..e’n
– базис в V'.
Зададим φ: x=∑ξiei =>
x’=∑ξie’i .
Ну и изоморфизм ли φ? 1) φ(x+y) = φ(∑ξiei+∑hiei
) = ∑(hi+ξi)e’i
= ∑ξie’i+∑hie’i
= φ(x)
+ φ(y)
2)φ(αx)=
φ(∑αξiei)=∑αξie’i
= α∑ξie’i
= αφ(x).
Из этих двух фактов имеем, что φ –
изоморфизм и V=~V’
Необх-ть:
пусть V=~V’
и φ – изоморфизм. Предположим, n>n'.
e1..en
= E
- базис в V.
ei’=
φ(ei)
![]() V’;
e1’...en’
– лз в V', т.к. n>n',
т.е. сущ-т α1..
αn
V’;
e1’...en’
– лз в V', т.к. n>n',
т.е. сущ-т α1..
αn
![]() P
: ∑αie’i
= Θ’. ∑αie’i
= ∑αi
φ(ei)
= φ(∑αiei)
= Θ’ => ∑αiei
= Θ => e1...en
– лз, но это противоречит тому, что
e1...en
– базис. Значит, предп-е, что n>n' неверно
=> n≤n’.
Но если, n<n' и e’1..e’n
= E’
- базис в V’
(ei’=
φ(ei)
P
: ∑αie’i
= Θ’. ∑αie’i
= ∑αi
φ(ei)
= φ(∑αiei)
= Θ’ => ∑αiei
= Θ => e1...en
– лз, но это противоречит тому, что
e1...en
– базис. Значит, предп-е, что n>n' неверно
=> n≤n’.
Но если, n<n' и e’1..e’n
= E’
- базис в V’
(ei’=
φ(ei)
![]() V’),
имеем e1...en
– лз в V', т.к. n>n',
т.е. сущ-т α1..
αn
V’),
имеем e1...en
– лз в V', т.к. n>n',
т.е. сущ-т α1..
αn
![]() P
: ∑αiei
= Θ. ∑αie’i
= ∑αi
φ(ei)
= φ(∑αiei)
= Θ’ т.к. ∑αiei
= Θ => e'1...e’n
– лз, но это противоречит тому, что
e’1...e’n
– базис. Значит, предп-е, что n<n' неверно
=> n’≤n.
Итак, мы имеем одновременно n’≤n
и n≤n’
значит, n=n, чтд.
P
: ∑αiei
= Θ. ∑αie’i
= ∑αi
φ(ei)
= φ(∑αiei)
= Θ’ т.к. ∑αiei
= Θ => e'1...e’n
– лз, но это противоречит тому, что
e’1...e’n
– базис. Значит, предп-е, что n<n' неверно
=> n’≤n.
Итак, мы имеем одновременно n’≤n
и n≤n’
значит, n=n, чтд.
26. Прямая сумма и прямое дополнение. Теорема о прямом дополнении. Теорема о размерности суммы подпространств.
WcV – ЛПП. W1+W2
= {x|
x=x1+x2,
x1![]() W1,
x2
W1,
x2![]() W2}
– сумма ЛПП. W1
W2}
– сумма ЛПП. W1![]() W2={x|
x
W2={x|
x![]() W1,
x
W1,
x![]() W2}
W2}
Опр.
Сумма ЛПП W1
иW2
наз-ся прямой (W1![]() W2)
если W1
W2)
если W1![]() W2
= {Θ}
W2
= {Θ}
Опр.
W1,
W2
– ЛПП, W1сW.
ЛПП W2
наз-ся прямым
дополн-м к W1
отн-но W,
если W= W1![]() W2
W2
Трм.
(О прям.доп). Пусть W1,W
– ЛПП. dimW=m, dimW1=k<m.
Тогда сущ-т W2
- прямое-доп-е к W1
отн-но W и dimW2=m-k.
Д-во Пусть
e1...ek
– базис в W1
тогда по трм о пополн. базиса сущ-т
gk+1...gm
такие, что (e1...ek,
gk+1...gm)-базис
в W. W2
= Z(gk+1...gm).
x![]() W:
x=ξ1e1+...+ξkek
+ hk+1gk+1+...+hmgm
= x1+x2
(x1
W:
x=ξ1e1+...+ξkek
+ hk+1gk+1+...+hmgm
= x1+x2
(x1![]() W1
; x2
W1
; x2![]() W2).
W=W1+W2.
x
W2).
W=W1+W2.
x![]() W1
W1![]() W2
=> x=
ξ1e1+...+ξkek
= hk+1gk+1+...+hmgm
=> ξ1=...=ξk=0=>
x=
Θ. W1
W2
=> x=
ξ1e1+...+ξkek
= hk+1gk+1+...+hmgm
=> ξ1=...=ξk=0=>
x=
Θ. W1![]() W2=W;
dimW1+dimW2=dimW.
W2=W;
dimW1+dimW2=dimW.
Трм (О
разм-ти суммы ПП) Пусть W1иW2
– конечномерные
ЛПП. Тогда
dim(W1+W2)=dim(W1)+dim(W2)-dim(W1![]() W2).
Док-во
M=
W1
W2).
Док-во
M=
W1![]() W2
– ЛПП.
McW2=>cущ-т
прям.
дополн
к
М
отн-но
W2.
Т.е.
сущ-т
ЛПП
P: P
W2
– ЛПП.
McW2=>cущ-т
прям.
дополн
к
М
отн-но
W2.
Т.е.
сущ-т
ЛПП
P: P![]() M=W2,
dimW2=dimP+dimM.
W1+W2=W1+(P
M=W2,
dimW2=dimP+dimM.
W1+W2=W1+(P![]() M)
= (W1+M)
M)
= (W1+M)
![]() P
= W1
P
= W1![]() P
=> dim(W1+W2)=dimW1+dimP=dimW1+dimW2
–
dimM = dimW1+dimW2
–
dim(W1
P
=> dim(W1+W2)=dimW1+dimP=dimW1+dimW2
–
dimM = dimW1+dimW2
–
dim(W1![]() W2).
W2).
27.Cкалярное произв-е векторов: определение и св-ва. Евклидово пространство, примеры.
Скалярное произведение (СП) – это ф-ция VxV->R и удовл. усл-ям: 1)(x,y)=(y,x) 2)(x+y,z)=(x,z)+(y,z) 3)(αx,z)= α(x,z) 4)(x,x)≥0, (x,x)=0=>x=Θ. (NB 1) из усл-й 2 и 3 сл-т утв-е (αx+βy,z)= α(x,z)+ β(y,z) 2)Псевдоскал-е пр-е – это когда 4) выглядит так: (x,x) ≥0).
Cв-ва:
1)(Θ,x)=0 2)(x,
αy+βz)=
α(x,y)+β(x,z)
3)(x,y)\|x||y|
= cosφ;
![]() =
|x|
4)|(x,y)|≤|x||y|
5)|x+y|≤|x|+|y|
Док-во:
1)(Θ,x)=
(0*y,x)=0(y,x)=0
2)
(x,
αy+βz)=
(αy+βz,
x)
= α(y,x)+β(z,x)
= α(x,y)+β(x,z).
3) 4) 0≤(x+ty,
x+ty)
= (x,x)+2t(x,y)+t2(y,y)≥0
=> D\4
= (x,y)2
– (x,x)(y,y)≤0
=> (x,y)2≤|x|2|y|2
=>|(x,y)|≤|x||y|.
5)|x+y|2
= (x+y,x+y)
= (x,x)
+ 2(x,y)
+ (y,y)
≤ x2
+ 2|x||y|
+ y2
= (|x|+|y|)2=>|x+y|≤|x|+|y|.
=
|x|
4)|(x,y)|≤|x||y|
5)|x+y|≤|x|+|y|
Док-во:
1)(Θ,x)=
(0*y,x)=0(y,x)=0
2)
(x,
αy+βz)=
(αy+βz,
x)
= α(y,x)+β(z,x)
= α(x,y)+β(x,z).
3) 4) 0≤(x+ty,
x+ty)
= (x,x)+2t(x,y)+t2(y,y)≥0
=> D\4
= (x,y)2
– (x,x)(y,y)≤0
=> (x,y)2≤|x|2|y|2
=>|(x,y)|≤|x||y|.
5)|x+y|2
= (x+y,x+y)
= (x,x)
+ 2(x,y)
+ (y,y)
≤ x2
+ 2|x||y|
+ y2
= (|x|+|y|)2=>|x+y|≤|x|+|y|.
Опр-е: Евклидово
простр-во E – ЛП V c заданным СП. Примеры:
1. E=Rn,
x=(ξ1...
ξn)
y=(h1...hn) ;
(x,y)=∑ξihi,
|x|=(ξ12,...,ξn2)1\2
2) E=C[ab],
x=x(t)
– непр-я на [ab]
ф-ция. (x,y)=![]() ;
|(x,y)|2=
(
;
|(x,y)|2=
(![]() )2
≤
)2
≤
![]() *
*![]() =
|x2||y2|;
[ ∑(ξihi)2
≤ ∑ξi2∑hi2
] 3)
E=R2
x=(ξ1,ξ2)
a)(x,y)=ξ1h1+
ξ2h2
б)(x,y)=ξ1h1
в) (x,y)=ξ1h2+
ξ2h1
=
|x2||y2|;
[ ∑(ξihi)2
≤ ∑ξi2∑hi2
] 3)
E=R2
x=(ξ1,ξ2)
a)(x,y)=ξ1h1+
ξ2h2
б)(x,y)=ξ1h1
в) (x,y)=ξ1h2+
ξ2h1
29.Теор (О существовании ОНБ)
Опр1: (g1...gn) = G – ОБ, если (gn, gi)=0, i=1,(n-1) Опр2: (e1...en)=E – ОНБ если это ОБ и |ei|=1, i=1,n
Во всяком конечномерном пространстве существует ОНБ
Док-во: Пусть (f1, f2, … fn)=F – базис в E
Проведём процесс ортогонализации:

Тогда имеем, что (gngk)=0 k=1,n-1
(g1,g2…gn) – ОБ в E
![]() k=1,n
k=1,n
получаем, (e1,…ek)-ОНБ
28. Ортогональность векторов. Теорема о связи ортогональности и линейной зависимости.
Опред: Векторы x, y называются ортогональными если (х,у) =0 (х┴у)
замеч: 1) Θ┴х х Е
2) если х┴у у то х= Θ
Система векторов g1...gn ортогональна если (gigj)=0 ij и ортонормированна если |gi|=1 i=1,n
Теор(Об ортогональности системы векторов)
Если g1, g2…gn – ортогональная система ненулевых векторов, то она линейно независима.
Док-во:
1g1+2g2+…+ngn= Θ |*gk
1 (g1gk)+…+ k(gkgk)+…+ n (gngk)= 0+0+...+ k(gkgk)+0+...+0 = k(gkgk)
с другой стороны, это равно Θ => k(gkgk)= Θ причем gk0 k=0 значит
g1, g2…gn – ЛНЗ.
30,Матрица Грама, свойства.
(f1,
f2,
… fn)=F–
базис в E
![]()
![]()
(x,y)=(
![]()
![]() )=
)=![]()
((fifj))ij=1,n=Г(F)-матрица Грамма
если Е=(e1,e2…en)-ОНБ то
 -
единичная матрица.
-
единичная матрица.
Св-ва Г(F)
Г(F)=ГT(F)
det Г(F)=0 (f1, f2, … fn) – линейно зависимы.
Если (f1, f2, … fn)=F - линейно не зависимы, то detГ(F)>0
Док-во
1) из определения. Г(F) = ((fi,fj)) = ((fj,fi)
2) (достат.) (f1, f2, … fn) – линейно зависимы ненулевой набор 1+2+…+n R
1f1+2f2+…+nfn= | fk , k=1,n =>

Г(Е)=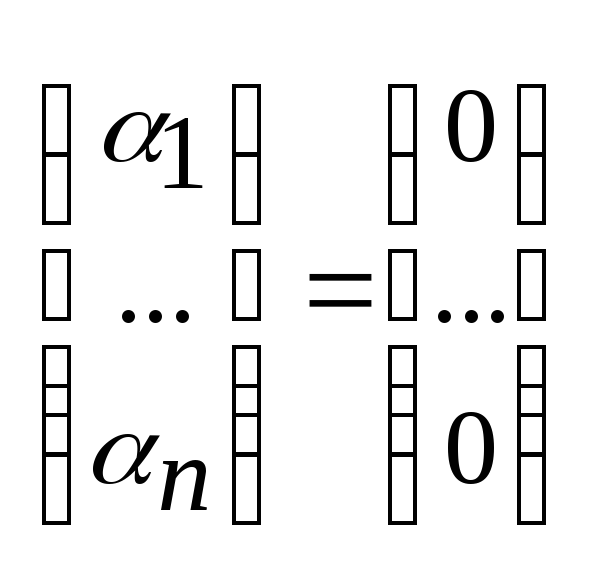 и1...
n
0
det Г(F)=0
и1...
n
0
det Г(F)=0
(необход.) для док-ва достаточно пойти в обратном направлении в док-ве достаточности.
3) Пусть (f1, f2, … fn)=F - базис в Z (f1, f2, … fn) ОНБ (e1, e2, … en)=Е
пусть S- матрица перехода от Е к F т.е F=E*S
Г(F)=Fт*F,
т.е

Г(F)=FT*F=(E*S)T*E*S=ST*ET*E*S=ST*I*S=ST*S
DetГ(F)=det (ST*S)= detST*detS=(detS)2>0
31. Линейные операторы ( ЛО ) в ЛП: определение, свойства, примеры. Ядро и образ ЛО.
Пусть V, W – ЛП над полем P. Oпр: Ф-ция A:VW наз-ся линейной, если для (x,yV, ,βP):( A(x+βy) = Ax+β Ay ); Если W=P, A – линейная форма, если W=V, то A – линейный оператор (ЛО). Опр: Образ ЛО A – Im A = {yV:Ax=y, xV}; Ядро ЛОA – KerA={xV, Ax=0}; Ранг ЛО – rangA = dim(Im(A));
примеры:
1)V=Pn
– ЛП многочленов. ЛО D
= d\dt;
Dx=x’(t);
2)Пусть V=V1![]() V2,
x=x1+x2
; A
– оператор проекции на V, если Ax=x;
3)N – нулевой оператор, если Nx=,
xV
V2,
x=x1+x2
; A
– оператор проекции на V, если Ax=x;
3)N – нулевой оператор, если Nx=,
xV
Cв-ва:
1)
A
=
2)
A(![]() )
=
)
=
![]() 3)
x1...xm
– ЛЗ => Ax1...Axm
– ЛЗ 4)
rangA
dimV;
Док-во:
1)
A
= A(0*x)
= 0*(
Ax)
= ;
2) из определения. 3) x1...xm
–
ЛЗ => ненулевой
набор 1...
m
такой, что 1x1+...+xmm
=
тогда и A(1x1+...+xmm)=
=> 1Ax1+...+
mAxm=
=> Ax1...Axm
– ЛЗ
4)Пусть dimV = n =>(x1...xn+1)
– ЛЗ => Ax1...Axn+1
– ЛЗ => dim(ImA)
= rangA
<
n+1 => rangA
≤ n = dimV;
3)
x1...xm
– ЛЗ => Ax1...Axm
– ЛЗ 4)
rangA
dimV;
Док-во:
1)
A
= A(0*x)
= 0*(
Ax)
= ;
2) из определения. 3) x1...xm
–
ЛЗ => ненулевой
набор 1...
m
такой, что 1x1+...+xmm
=
тогда и A(1x1+...+xmm)=
=> 1Ax1+...+
mAxm=
=> Ax1...Axm
– ЛЗ
4)Пусть dimV = n =>(x1...xn+1)
– ЛЗ => Ax1...Axn+1
– ЛЗ => dim(ImA)
= rangA
<
n+1 => rangA
≤ n = dimV;
ЛО в конечномерных ЛП. Матрица ЛО, ранг ЛО, замена базиса.
A:RnRn
(e1,
e2,
… en)=E
в
Rn ;
 .
Пусть y=Ax
– образ. Теперь пусть
.
Пусть y=Ax
– образ. Теперь пусть
![]()
…
![]()
тогда A= -
матрица линейного оператора A
в E
-
матрица линейного оператора A
в E
![]() -
координаты Ae1.
-
координаты Ae1.
![]() -
координатыAen
-
координатыAen
 -координаты
x
в E.
-координаты
x
в E.
 - координатыy
в E
- координатыy
в E
y=Ax
y(e)=Ax(e)
Переход к другому базису:
(e1, e2, … en)=e в Rn
(e’1, e’2, … e’n)=e’
 - матрица перехода
от e
к e’
- матрица перехода
от e
к e’
![]() -координатыe’1
-координатыe’1
e’=e*S
предположим что A1 A’ - матрицы Л.О в e и e’ x(e) y(e) – координаты x, y в e
x(e’) y(e’) – координаты x, y в e’
x=ex(e) y=Ax
x(e)=Sx(e’)x(e’)=S-1x(e)
y=ey(e)=eAx(e)=e’y(e’)=eSA’*x(e’)=e[SA’S-1]x(e) (A=SA’S-1) и (A’=S-1*A*S)
Теор (О ранге Л.О)
Пусть (e1, e2, … en)=e - базис в Rn. A-матрица Л.О A в e тогда rangA=rangA
Док-во:
RangA=dim(ImA); ImA=Z(g1,g2,…,gn) где gi=Aei i=1,n
rangA=dim Z(g1,g2,…,gn)=rang(g1(e),…,gn(e))=rangA
