Распределение Вейбулла

Двухпараметрическое распределение Вейбулла является более гибким, чем экспоненциальное, которое может рассматриваться как частный случай первого. Плотность распределения Вейбулла

. (8)

При 1/t₀ =  и m = 1 уравнение (8) превращается в плотность экспоненциального распределения. Величина 1/t₀ определяет масштаб, а m – асимметрию (форму) распределения.

После интегрирования (8) от 0 до t получаем функцию распределения F(t), равную Q(t) :

. (9)

Следовательно, . (10)

Отношение плотности (8) и вероятности (10) даёт интенсивность отказов

. (11)

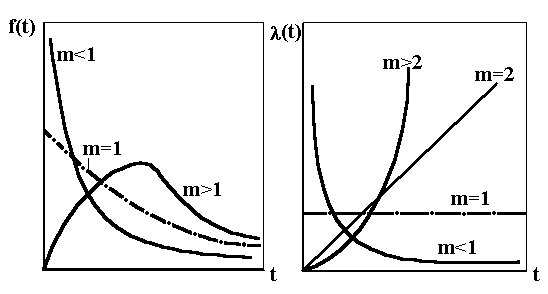
Основные графики распределения Вейбулла показаны на рис.4.

Двухпараметрическое распределение Вейбулла обладает исключительной гибкостью при аппроксимации эмпирических распределений и поэтому широко применяется в практических приложениях теории надёжности. Оно используется при описании законов надежности, как на участке приработки, так и при анализе процессов старения и износа.

Средняя наработка на отказ при распределении Вейбулла определяется из условия

а) б)

Рис.3.4. Графики распределения Вейбулла

и равна

, (12) где - гамма – функция; .

Нормальное распределение

Двухпараметрическое нормальное (гауссово) распределение исключительно широко применяется в практических задачах теории надёжности. Параметрами этого распределения является  – математическое ожидание случайной величины и  - среднеквадратическое отклонение. Плотность нормального распределения определяется зависимостью

. (13)

Функция распределения F(x) (рис.3.5) при нормальном законе определяется интегралом от плотности f(x) с пределами интегрирования от -  до + .

Случайная величина t как и во всех задачах надёжности имеет смысл наработки объекта и поэтому определена на положительной полуоси чисел, а нормальный закон, как уже отмечалось, определён на всей числовой оси от -  до + . В связи с этим в теории надёжности рассматривают усечённый нормальный закон, плотность которого определяется путём умножения (3.13) на постоянный множитель

,

где , a, b – левая и правая границы усечённого распределения.

F(a),F(b) – значения функций распределения нормального закона на левой и правой границах усечения.

Смысл постоянного множителя с становится ясным при рассмотрении графика плотности нормального распределения, представленного на рис.6.

Рис.5. Плотность и функция распределения нормального закона при математическом ожидании  =0 и среднеквадратическом отклонении  =1.

Известно, что площадь под кривой плотности распределения всегда должна быть равна единице, то есть в данном случае . Как показано на рис.6 для обеспечения этого условия кривую плотности усечённого нормального закона приходится сдвигать вверх и вправо путём умножения исходной плотности нормального закона на постоянный множитель. Соответственно будут меняться основные параметры: математическое ожидание и среднеквадратическое отклонение. Расчёты показывают, что при отношении / < 0.5 (коэффициент вариации) постоянный множитель c для усечённо- нормального закона близок к единице. Поэтому во многих практических задачах теории надёжности пользуются параметрами нормального закона распределения случайной наработки объекта до отказа. При этом математическое ожидание  отождествляют со средней наработкой до отказа Т₀.

Рис.6. Плотности нормального и усечённо – нормального распределений при  = 2,  = 3. Параметры усечения a=0, b=10.

Вероятность безотказной работы при нормальном распределении равна

. (14)

Вероятность отказа рассчитывается по формуле (при с  1)

. (15)

Интенсивность отказов определяется отношением плотности к вероятности безотказной работы

. (16)

Интегралы в выражениях (14)…(16) не выражаются через элементарные функции. Обычно они представляются через интеграл вероятности от параметра

z = (t-T₀)/

, (17) для которого составлены таблицы.

С учётом (17) вероятность безотказной работы при нормальном законе определяется по формуле

. (18)

1 Червоный А.А., Лукьященко В.И., Котин Л.В. Надёжность сложных систем. Изд.2-е, перераб. и доп.-М.: Машиностроение. 1976.

11

- -