ЛЕКЦИЯ №48
17.2. Интегральная и дифференциальная форма закона полного тока
Количественная
связь между циркуляцией вектора
по замкнутому контору и током внутри
контура определяется законом полного
тока в интегральной форме:
(17.3)
Линейный интеграл от напряженности магнитного поля вдоль любого замкнутого контура равен полному току, пронизывающему замкнутый контур.
Интегральную форму закона полного тока применяют, когда может быть использована симметрия в поле. Определим напряженность поля в некоторой точке А в поле уединенного прямого провода с током I (рис. 17.3).
Рис. 17.3. к определению напряженности поля уединенного провода
Проведем через точку А окружность радиусом R в плоскости, перпендикулярной оси провода, так что центр ее находится на этой оси. В силу симметрии напряженность поля во всех точках окружности численно одна и та же. Направление напряженности совпадает с касательной к окружности:
;
.
(17.4)
Если какое-либо поле имеет сложный характер и напряженность H нельзя вывести из-под знака интеграла, то использовать закон полного тока в интегральной форме так просто не удается.
Соотношение (17.3) пригодно для контура любых размеров, в том числе и для весьма малого.
Выделим в какой-либо
среде небольшой контур и составим вдоль
него циркуляцию вектора
(рис 13.4).
Рис. 17.4. К нахождению
циркуляции вектора
для любого контура
Если площадь мала,
то можно полагать, что плотность тока
в пределах этой площади одинакова, и
тогда ток, пронизывающий площадь:
,
Разделим обе части равенства на s и устремим s к нулю. Возьмем предел полученного соотношения:
Если площадь
ориентирована перпендикулярно к
,
то
(17.6)
Формула (17.6) называется законом полного тока в дифференциальной форме.
Ротор – это функция, характеризующая поле в рассматриваемой точке, в отношении способности к образованию вихрей. Раскрытие функции ротора в декартовой системе координат мы рассмотрели в параграфе 14.1.3 формулы (12.17), (12.18) и (12.19).
17.3. Принцип непрерывности магнитного потока
и запись его в дифференциальной форме
Магнитный поток – это поток вектора магнитной индукции через некоторую поверхность:
(17.7)
Если поверхность замкнута, то
(17.8)
Это математическая запись принципа непрерывности магнитного потока.
Разделим обе части (17.8) на объем V, находящийся внутри замкнутой поверхности s, и найдем предел отношения, когда V стремится к нулю:
(17.9)
Соотношение (17.9)
можно трактовать как дифференциальную
форму принципа непрерывности магнитного
потока. В любой точке магнитного поля
нет ни истока, ни стока линий вектора
магнитной индукции. Линии вектора
нигде не прерываются, они представляют
собой замкнутые сами на себя линии.
17.4. Скалярный потенциал магнитного поля
Вихревыми принято
называть поля, в которых ротор векторной
величины, описывающей поле, отличен от
нуля. Так, для магнитного поля постоянного
тока
,
поэтому во всех точках пространства,
где
,
поле вектора
является вихревым. В областях пространства,
где J
= 0,
,
магнитное поле можно рассматривать как
потенциальное, т.е. как такое поле, каждая
точка которого имеет скалярный магнитный
потенциал
.
(17.10)
Так как
,
то при a
= const
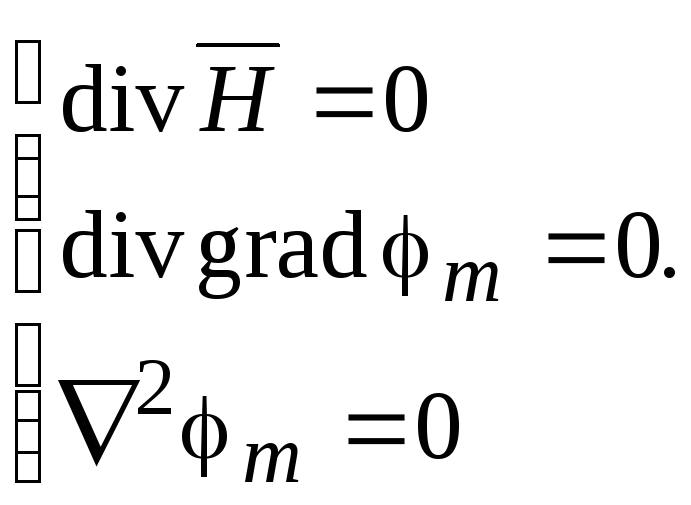(17.11)
Скалярный потенциал
магнитного поля
подчиняется уравнению Лапласа.
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2.
17.5. Граничные условия
В магнитном поле постоянного тока выполняются следующие граничные условия:
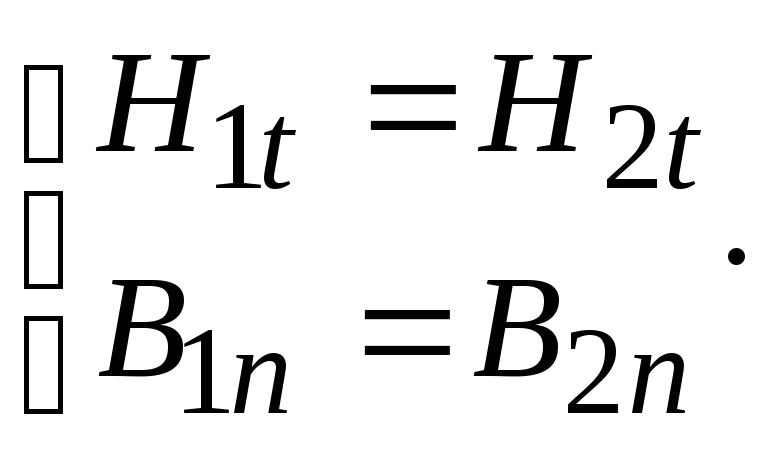(17.12)
На границе раздела двух однородных и изотропных сред, различных в магнитном отношении (различные r) равны тангенциальные составляющие векторов напряженности магнитного поля и нормальные составляющие магнитных индукций на границе раздела.
Условие (17.12) не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. Под ним понимают ток, протекающий по бесконечно тонкому плоскому проводнику, положенному на границе раздела.
17.6. Векторный потенциал магнитного поля
Векторный потенциал
магнитного поля
– это векторная величина, плавно
изменяющаяся от точки к точке, ротор
которой равен магнитной индукции
(17.13)
Основанием для представления индукции в виде ротора от вектора-потенциала служит то, что дивергенция любого ротора тождественно равна нулю, т.е.
Если вектор-потенциал как функция координат известен, то индукцию в любой точке поля определяют путем нахождения ротора от вектора-потенциала в соответствии с (17.13). Векторным потенциалом можно пользоваться и для областей, занятых током.
В электротехнических расчетах векторный потенциал применяют для двух целей:
1. Определения вектора магнитной индукции по формуле (17.13);
2. Определения магнитного потока, пронизывающего какой-либо контур.
Векторный потенциал в произвольной точке поля связан с плотностью тока в этой же точке уравнением Пуассона.
Умножим обе части (17.6) на a. Если магнитная проницаемость постоянна, то ее можно внести под знак ротора:
; (17.14)
;
;
rot rot A = [V[VA]] = grad div A - V2A = mad.
Так как
есть расчетная функция, то в магнитном
поле постоянного тока ее можно подчинить
требованию:
(17.15)
Это требование
означает, что линии вектора
есть замкнутые сами на себя линии:
.
(17.16)
Уравнение (17.16)
представляет собой уравнение Пуассона.
В отличие от уравнения (13.21), составленного
относительно скалярной величины ,
уравнение (17.16) составлено относительно
векторной величины
.
Общее решение по аналогии может быть
записано как
(17.17)
Единицей измерения
является Вс/м.
Формула (17.17) дает общее решение уравнения
(17.16). Вектор
в любой точке поля можно определить
вычислением объемного интеграла (17.17).
Последний должен быть взят по всем
областям, занятым током. Следует отметить,
что взятие интеграла правой части
формулы (17.17) сопряжено обычно со
значительными математическими выкладками.
17.7. Выражение магнитного потока через циркуляцию вектора-потенциала
Магнитный поток, пронизывающий какую-либо поверхность:
(17.7)
На основании теоремы Стокса поверхностный интеграл может быть преобразован в линейный
(17.18)
Для определения
магнитного потока, пронизывающего
некоторую площадь (поверхность) s,
необходимо подсчитать циркуляцию
вектора потенциала
по замкнутому контуру, на который
опирается поверхность s.
Определение потока
по (17.18) часто имеет преимущества по
сравнению с определением потока через
магнитную индукцию (17.7). Соотношением
(17.7) можно пользоваться в том случае,
когда известно значение
в любой точке поверхности s,
тогда как для вычисления потока с помощью
соотношения (17.18) достаточно знать
значение
на контуре и не требуется значения
в точках внутри контура.
Рассмотрим граничные условия для векторного потенциала.
.
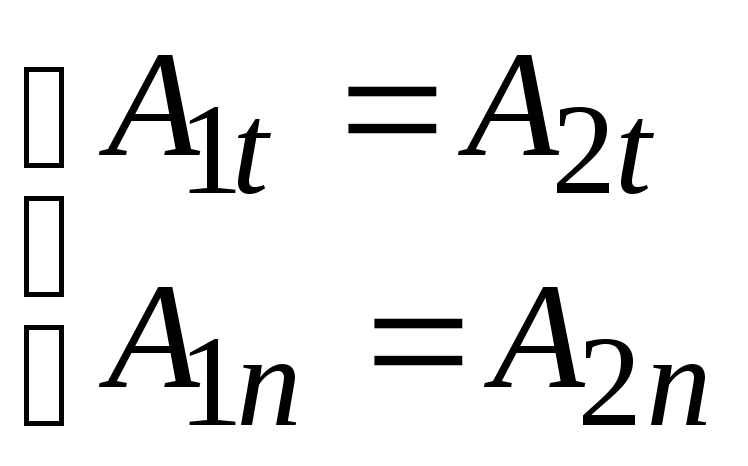(17.19)
17.8. Расчет магнитного поля одиночного проводника с током
Требуется рассчитать магнитное поле внутри и за пределами проводника (рис. 17.5). Это означает, что необходимо определить распределение напряженности и вектора-потенциала.
Рис. 17.5. К расчету магнитного поля одиночного проводника
Для расчета используем закон полного тока в интегральной форме
Рассчитаем
циркуляцию вдоль окружности, центр
которой совпадает с центром провода.
При этом напряженность в любой точке
этой окружности
постоянна по модулю и совпадает с
направлением элементарного участка
dl.
Внутри проводника
(
)
.
Следовательно, внутри проводника напряженность магнитного поля определяется выражением
.
Максимальное значение напряженности магнитного поля имеет место на поверхности проводника
Вне проводника
(
)
закон полного тока можно записать в
виде
.
При этом распределение напряженности
происходит по закону
.
Распределение напряженности магнитного поля внутри и вне проводника показано на рис. 17.6.
Рис. 17.6. Распределение магнитного поля одиночного проводника