
ЛЕКЦИЯ №52
18.7. Электрический поверхностный эффект
Рассмотрим проводник в виде шины (рис.18.8). Предположим, что 2a<<h, h<<l. По проводнику протекает ток I. В любом поперечном сечении характер распределения напряженности магнитного поля одинаков.
Требуется выяснить распределение напряженности электрического и магнитного полей по сечению шины.
Так как у шины имеется две границы, то могут возникать прямые и обратные волны. Поэтому решение дифференциальных уравнений второго порядка имеет вид:
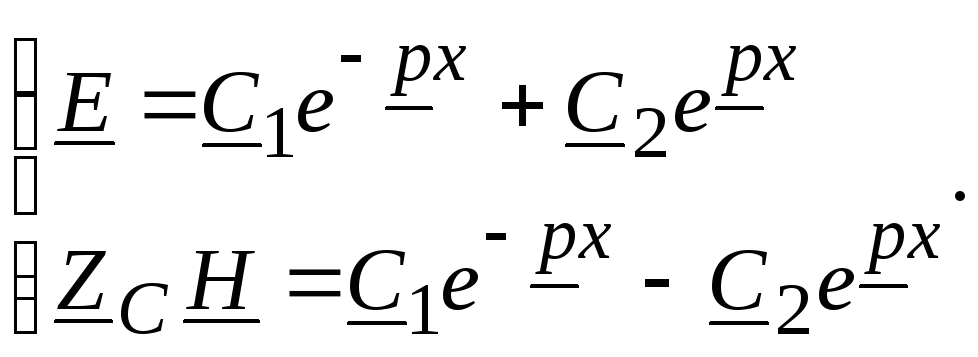 (18.26)
(18.26)

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 18.8. Электромагнитное поле в проводнике с током
Разместим начало системы координат посредине шины и сориентируем ее таким образом, чтобы векторы напряженностей электрического и магнитного полей имели составляющие только по одной координате.
Постоянные интегрирования определим из граничных условий:
- при x=-a H=H0;
- при x=a H=-H0.
Тогда из системы уравнений (18.26) следует:

Последовательной подстановкой получаем:

Следовательно,
![]() (18.27)
(18.27)
Подставив эти значения в уравнения (18.26), получим
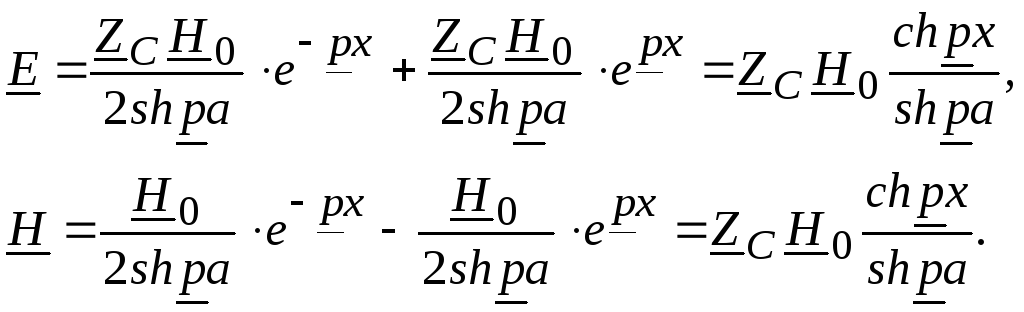
Учитывая, что на границе шины
![]()
получим
![]()
Окончательно мы имеем
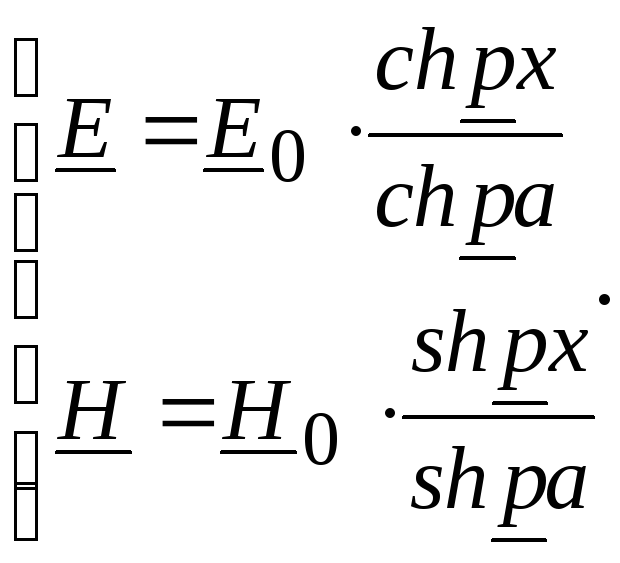 (18.28)
(18.28)
Рассмотрим, как изменяются соотношения E/E0 и H/H0 по сечению шины. Так как коэффициенты затухания и фазы для проводящей среды равны, то
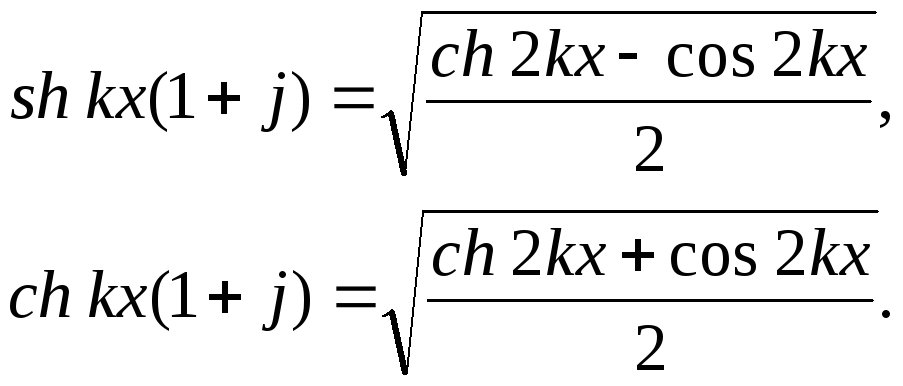
Тогда
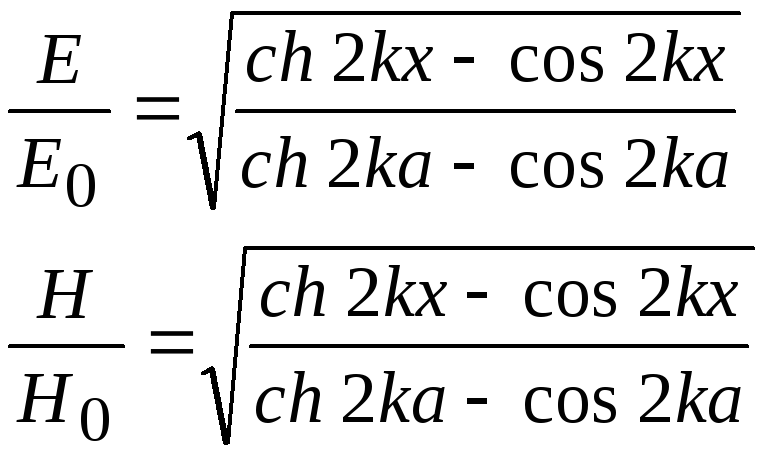 , (18.29)
, (18.29)
![]()
Так как величина a является числом, то характер зависимостей E/E0 и H/H0 определяется характеристиками материала шины и частотой. Эти зависимости представлены на рис. 18.9.
Так как ch p·0≠0, то напряженность электрического поля не уменьшается до нуля. В то же время sh p·0=0, поэтому напряженность магнитного поля в середине шины (при x=0) равна нулю.
![]() 2ka=0
2ka=0

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 18.9. Зависимости E/E0 и H/H0 от толщины шины
При ω=0 (постоянный
ток) величина напряженности электрического
поля определяется вектором плотности
тока
![]() и не зависит от положения рассматриваемой
области. Аналогичная картина наблюдается
при частотах, близких к нулю. В этом
случае говорят о квазистатическом
распределении поля.
и не зависит от положения рассматриваемой
области. Аналогичная картина наблюдается
при частотах, близких к нулю. В этом
случае говорят о квазистатическом
распределении поля.
При повышении частоты картина распределения плотности тока, а, следовательно, и напряженности электрического поля меняется. Большее значение напряженностей наблюдается по края пластины и спадает во внутренней части. Возникает поверхностный эффект.
В другом случае (при ω→∞) ток будет протекать только по поверхности шины.
18.8. Магнитный поверхностный эффект
Рассмотрим поле
в стальном листе при прохождении вдоль
листа переменного магнитного потока
![]() (рис. 18.10). Лист имеет толщину 2a,
высоту h>>2a
и большую протяженность в направлении,
перпендикулярном рисунку. Средняя
плотность магнитного потока по сечению
листа
(рис. 18.10). Лист имеет толщину 2a,
высоту h>>2a
и большую протяженность в направлении,
перпендикулярном рисунку. Средняя
плотность магнитного потока по сечению
листа
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
а) б)
Рис. 18.10. Электромагнитное поле в проводнике с магнитным потоком
Задача состоит в
определении законов изменения
![]() и
и
![]() по сечению листа.
В силу симметрии напряженность магнитного
поля на левой стороне такая же, что и на
правой поверхности листа. Обозначим ее
через
по сечению листа.
В силу симметрии напряженность магнитного
поля на левой стороне такая же, что и на
правой поверхности листа. Обозначим ее
через
![]() и будем считать известной.
и будем считать известной.
Так как 2a<<h,
то искажающим влиянием краев листа на
поле можно пренебречь и считать, что в
лист с двух сторон проникает плоская
электромагнитная волна. Пусть напряженность
магнитного поля
![]() направлена по оси
x.
Тогда
направлена по оси
x.
Тогда
![]()
Из граничных условий найдем постоянные интегрирования.
При z=-a ![]() (18.30)
(18.30)
При z=a ![]() (18.31)
(18.31)
Совместное решение
(18.30) и (18.31) относительно
![]() и
и
![]() дает
дает
![]() (18.32)
(18.32)
В произвольной точке
![]()
![]() (18.33)
(18.33)
Напряженность электрического поля:
![]()
где
![]() (18.34)
(18.34)
При z=+a
напряженность
![]() направлена вверх,
при z=-a
– вниз.
направлена вверх,
при z=-a
– вниз.
Вектор Пойнтинга направлен внутрь листа.
Ток, возникающий
при прохождении по листу переменного
магнитного потока, называют вихревым.
Вектор плотности вихревого тока
![]() в любой точке листа совпадает с вектором
в любой точке листа совпадает с вектором
![]() в этой же точке.
Магнитная индукция в произвольной
точке:
в этой же точке.
Магнитная индукция в произвольной
точке:
![]() (18.35)
(18.35)
Среднее значение индукции в листе:
![]() (18.36)
(18.36)
Если считать
![]() известной
и равной
известной
и равной
![]() то из (18.36) можно найти напряженность
поля на поверхности листа
то из (18.36) можно найти напряженность
поля на поверхности листа
![]() (18.37)
(18.37)
Напряженность поля в средней плоскости листа при z=0
![]()
Отношение:
![]()
Напряженность поля в средней плоскости может быть много меньше напряженности поля на поверхности листа. Неравномерное распределение поля по сечению проводящего тела, вызвано затуханием электромагнитной волны при ее распространении в проводящую среду, называемым поверхностным эффектом. Если вдоль листа направлен магнитный поток, то поверхностный эффект часто называют магнитным, если вдоль плоского листа направлен переменный ток, то – электрическим поверхностным эффектом. На рис. 18.7б показаны кривые: H(z) и E(z). H(z) до нуля не снижается, так как ch 0≠0/.
Для
![]() справедливо:
справедливо:
![]() и кривая проходит через нуль.
и кривая проходит через нуль.
Кривая плотности вихревых токов J=γE качественно повторяет кривую E(z).
