ЛЕКЦИЯ №50
18. ПЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
18.1. Определение переменного электромагнитного поля.
Основные уравнения
Под электромагнитным
переменным полем понимают совокупность
изменяющихся во времени и взаимно
связанных и обуславливающих друг друга
электрического и магнитного полей. Оно
определяется двумя векторными величинами:
напряженностью электрического поля
и напряженностью магнитного поля
.
(18.4)
Если выразить
индукции D
и H
через напряженности
то второе слагаемое уравнения (18.3)
запишется
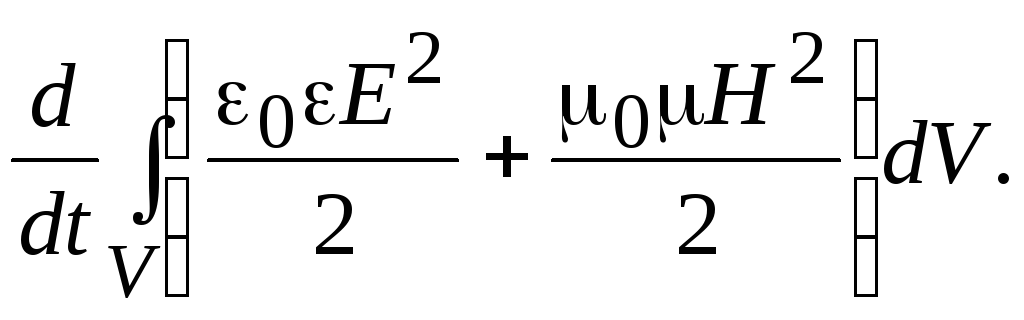
Тогда
(18.5)
Это уравнение представляет собой уравнение баланса энергии
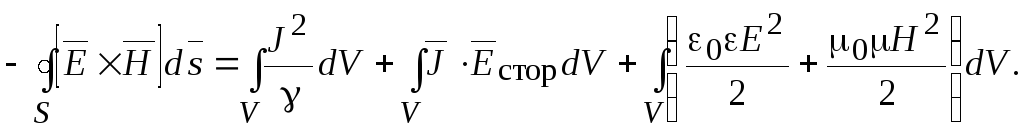
Векторное
произведение
обозначают
и называют вектором Пойнтинга.
Первое слагаемое показывает, какая энергия выделяется в данном объеме в виде тепла, второе – энергию сторонних сил, третье – изменение электрической и магнитной энергий.
Векторы
,
и
образуют правую тройку векторов (рис.
18.1).
Рис. 18.1. Взаимное расположение векторов
Вектор Пойнтинга характеризует плотность потока энергии и направление ее перемещения.
18.2. Передача энергии по коаксиальному кабелю
На рис. 18.2 показан отрезок коаксиального кабеля и расположенные относительно него составляющие электромагнитного поля.
Определим проекции
вектора Пойнтинга в цилиндрической
системе координат, так как вектор
напряженности магнитного поля ориентирован
по касательной к цилиндрическому
проводнику с током, т.е. в цилиндрической
системе координат имеет составляющую
только
,
то вектор Пойнтинга не будет иметь такой
проекции. При этом Пz=ErHα;
Пr=EzHα.
Рис. 18.2. Отрезок коаксиального кабеля
Напряженность электрического поля в диэлектрике определяется зарядом и током
Напряжение между жилами кабеля
.
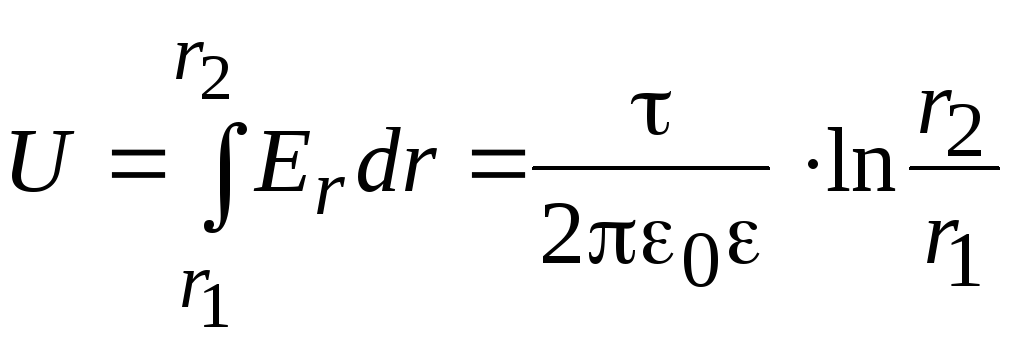Следовательно, на поверхности жилы
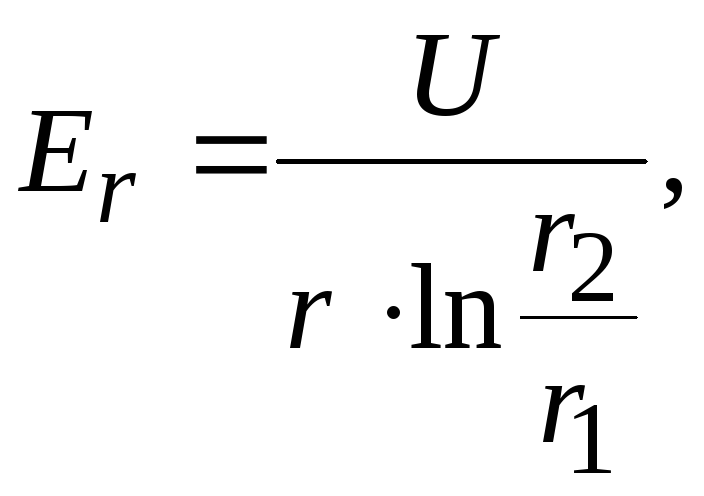
По закону полного
тока
Тогда
(18.6)
Из формулы видно, что плотность потока энергии имеет наибольшее значение вблизи жилы (рис. 18.3):
(18.7)
Рис. 18.3. К определению плотности тока энергии
За пределами кабеля магнитного поля нет (H=0).
В пределах оболочки нет радиальной составляющей вектора поля, следовательно, нет потока.
Угловая и радиальная составляющие напряженностей имеются только в кольцевом сечении диэлектрика.
Следовательно, энергия в осевом направлении передается по зазору в кабеле, а проводники служат как направляющие для потока.
Радиальная составляющая вектора Пойнтинга на поверхности жилы
(18.8)
Полагая, что плотность тока энергии на поверхности жилы одинакова, найдем энергию
(18.9)
т.к.
Следовательно, радиальная составляющая вектора Пойнтинга определяет потери энергии в проводнике при протекании по нему тока.
18.3. Уравнения для расчета электромагнитного поля
Запишем I и II уравнения Максвелла:
(18.10)
Известно, что
а также что в области, где нет свободных
зарядов,
Возьмем ротор системы уравнений (18.10):
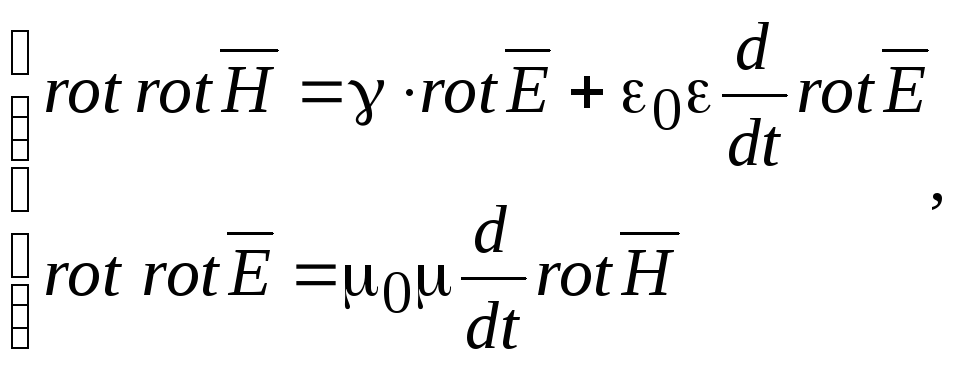
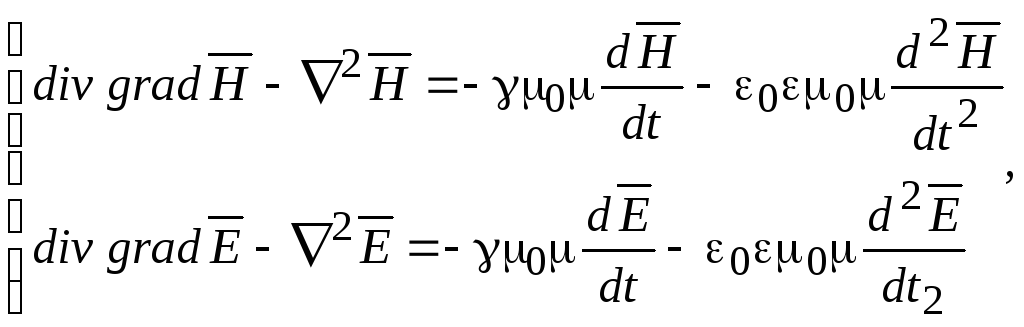
(18.11)
Эти уравнения показывают, как распространяется поле во времени и в пространстве.
Получение решения этих уравнений в общем виде невозможно. Поэтому решают некоторые частные случаи.
-
В случае проводящей среды (ε=0)
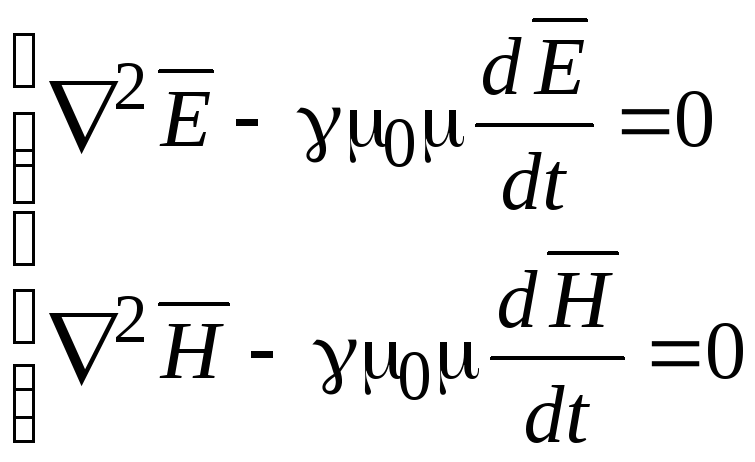(18.12)
Это уравнения теплопроводности.
-
В случае диэлектрика (γ=0) получаем
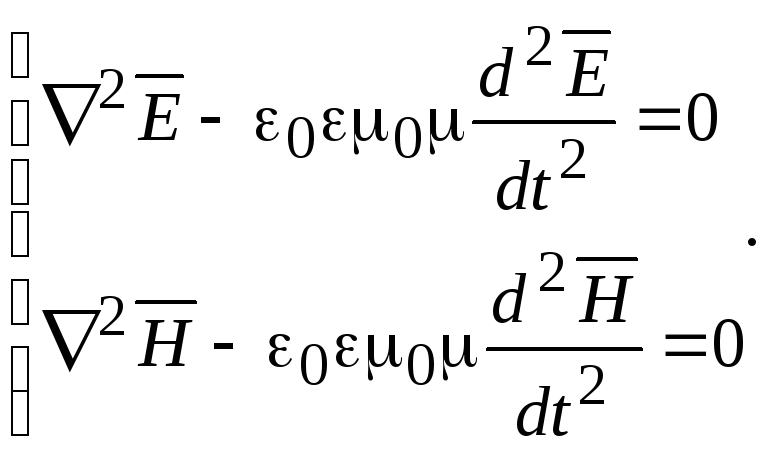(18.13)