
справочник по физике
.pdf= |
ст |
= |
ст , |
|
|
61 |
|
где Ест – напряженность поля сторонних сил.
ЭДС, действующая в замкнутой цепи, определяется как циркуляция вектора напряженности поля сторонних сил,
ЭДС на участке цепи 1-2 |
= ∫ |
ст |
. |
= |
ст |
. |
Помимо сторонних сил на заряд q0 действуют также силы
электростатического поля
FE = q0E .
Сила, действующая в проводнике на заряд q0, равна:
F = Fст + FE = q0(Eст + E) .
= |
∫ |
ст |
+ |
∫ |
|
|
= |
+ |
, |
|
|
|
(φ − φ ) |
||||||
Работа результирующей силы на участке 1-2: |
|
||||||||
для замкнутой цепи работа электростатических сил равно нулю, поэтому
A = q0 E12;
напряжение на участке 1-2
U12 = (ϕ1 − ϕ2 ) + E12,
т.е. напряжение есть алгебраическая сумма работ кулоновского и стороннего полей по перемещению единичного положительного заряда.
4.3. Сопротивление проводников
PDF created with pdfFactory Pro trial version www.pdffactory.com

62
Электрическое сопротивление
R = dUdI .
Сопротивление однородного линейного проводника длиной l и площадью поперечного сечения S
где r - удельное электрическое сопротивление.
Единица сопротивления 1 Ом.
1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток 1 А.
Единица удельного сопротивления 1 ом-метр (Ом × м).
Электрическая проводимость
Единица электрической проводимости 1 сименс (См).
1 См – проводимость участка электрической цепи сопротивлением 1 Ом.
Удельная электропроводимость:
Единица удельной электропроводимости 1 сименс на метр (См/м).
Зависимость сопротивления металлов от температуры:
r = r0 (1+ at) ,
R = R0 (1+ at) ,
где a – температурный коэффициент сопротивления; t – температура, °С.
PDF created with pdfFactory Pro trial version www.pdffactory.com

63
4.4. Последовательное и параллельное соединение проводников
Последовательное соединение |
Параллельное соединение |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
= |
R1 |
|
|
|
|
|
R |
|
|||
U |
2 |
|
|
|||
|
|
|
2 |
|
|
|
4.5. Закон Ома
Закон Ома для однородного участка цепи (не содержащего ЭДС):
сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника
Закон Ома в дифференциальной форме связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в той же точке:
Закон Ома для неразветвленной замкнутой цепи:
I = E /(R + r),
где R – сопротивление внешней цепи; r – внутреннее сопротивление источника.
PDF created with pdfFactory Pro trial version www.pdffactory.com

64
r E
R
Напряжение во внешнем участке цепи:
U = IR = E – Ir.
Ток короткого замыкания:
Iкз = E /r.
Закон Ома для батареи последовательно соединенных элементов с одинаковыми E и r:
I = nE /(R + nr).
где n – число элементов в батарее.
r |
|
E |
|
|
|
|
|
|
|
|
E1 = E2 =…= En |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
r1 = r2 = ... = rn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Закон Ома для батареи параллельно соединенных элементов:
I = Eрез /(R + rрез),
n |
1 |
|
|
|
|
n |
|
где 1/ rрез = å |
|
|
и Eрез/rрез = åEk/rk; n – число элементов в батарее. |
||||
rk |
|||||||
k |
|
|
|
k |
|||
|
I = |
|
Eε |
|
(при E1 = E2 =…= En; r1 = r2 = ... = rn ). |
||
|
|
R + |
r |
||||
|
|
|
|
n |
|||
|
|
|
|
|
|||
E, r
E, r
E, r
R
PDF created with pdfFactory Pro trial version www.pdffactory.com

65
Закон Ома для неоднородного (содержащего ЭДС) участка цепи (обобщенный закон Ома):
IR = (ϕ1 − ϕ2 ) + E12,
где E 12 – ЭДС, действующая на участке 1-2; (ϕ1 − ϕ2 ) − разность потенциалов точек 1 и 2; E12>0, если она способствует движению положительных зарядов; E12 <0, если она препятствует их движению.
4.6. Анализ обобщенного закона Ома (ОЗО)
1 |
Источника нет: |
Из ОЗО: |
Закон Ома для |
|
E12 = 0 |
|
однородного участка |
|
|
|
цепи |
2 |
Цепь замкнута |
Из ОЗО: |
Закон Ома для |
|
|
I = E /(R + r), |
замкнутой цепи |
|
|
где R – сопротивле- |
|
|
|
ние всей цепи |
|
3 |
Цепь разомкнута: |
Из ОЗО: |
ЭДС равна разности |
|
I = 0 |
E12 = ϕ2 − ϕ1 |
потенциалов на |
|
|
|
клеммах разомкнутого |
|
|
|
элемента |
|
4.7. Правила Кирхгофа для разветвленных цепей |
||
Узел электрической цепи – любая точка цепи, в которой сходится не менее трех токов. Токи, входящие в узел, считаются положительными, а токи, выходящие из узла, отрицательными.
Первое правило Кирхгофа:
алгебраическая сумма сил токов, сходящихся в узле, равна нулю
Второе правило Кирхгофа:
PDF created with pdfFactory Pro trial version www.pdffactory.com

66
в любом замкнутом контуре
n |
n |
åIi Ri =åEi. |
|
i=1 |
i=1 |
4.8. Работа и мощность тока
Элементарная работа электрического тока:
Работа электрического тока:
Единица работы 1 джоуль (Дж).
Внесистемная единица работы 1 кВтч = 3,6 МДж = 3,6×106 Дж.
Работа постоянного электрического тока:
A = Uq = IUt = I 2Rt = U 2 t .
R
Мощность электрического тока
Единица мощности 1 ватт (Вт).
Закон Джоуля-Ленца:
.
Закон Джоуля-Ленца для постоянного тока
Q = Uq = IUt = I 2Rt = U 2 t .
R
PDF created with pdfFactory Pro trial version www.pdffactory.com

67
Закон Джоуля-Ленца в дифференциальной форме:
где w - удельная тепловая мощность тока, т.е. количество теплоты, выделяющейся за единицу времени в единице объема проводника.
Коэффициент полезного действия источника тока (КПД):
η = |
Pпол |
= |
R |
= U |
|
|
R + r |
E |
|||
|
Рзатр. |
Е |
|||
|
|
||||
5. МАГНИТНОЕ ПОЛЕ
Основные формулы и определения
5.1. Основные характеристики магнитного поля
где a -
где
Момент сил, вращающий рамку с током в магнитном поле:
|
|
r |
r |
r |
= pmBsin α, |
|
|
|
M = [pmB], M |
|
|||
p |
|
– магнитный момент рамки с |
r |
- магнитная индукция; |
||
m |
током; B |
|||||
|
|
|
|
|
r |
|
угол между нормалью к плоскости контура и вектором B .
Магнитный момент рамки с током
S – площадь рамки; r - единичный вектор нормали к поверхности рамки. n
Магнитная индукция в некоторой точке поля равна отношению максимального момента сил, действующих на рамку с током, к магнитному моменту этой рамки:
Единица индукции магнитного поля 1 тесла (Тл = 1 Н/А × м).
Магнитное поле макротоков описывается вектором напряжен- r
ности Н , который связан с вектором магнитной индукции:
PDF created with pdfFactory Pro trial version www.pdffactory.com
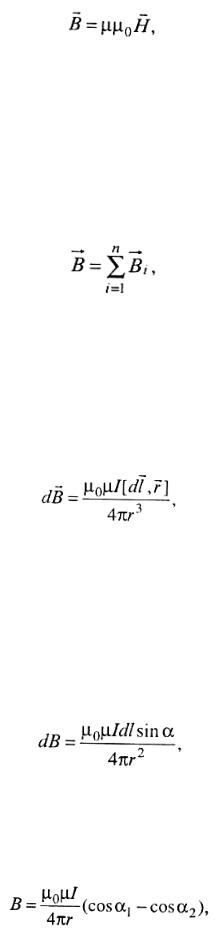
68
где m - магнитная проницаемость среды, m0 = 4p ×10−7 Гн/м – магнитная постоянная.
Принцип суперпозиции (наложения) магнитных полей: магнитная индукция поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых
каждым током или каждым движущимся зарядом в отдельности
5.2. Закон Био-Савара-Лапласа и его применение
r
Закон Био-Савара-Лапласа: индукция магнитного поля dB , создаваемого элементом тока I длиной dl, на расстоянии r от него равна
где r - радиус-вектор, проведенный из элемента dl в выбранную точку поля. r
r
Направление dB находится по правилу правого винта: если
поступательное движение винта соответствует направлению тока, то r
касательная к траектории головки винта дает направление dB .
Скалярная форма записи закона Био-Савара-Лапласа имеет вид:
r |
r |
где a - угол между dl |
и r . |
Магнитное поле прямолинейного тока:
PDF created with pdfFactory Pro trial version www.pdffactory.com

69
где α1, α2 − углы, под которыми из рассматриваемой точки поля видны начало и конец тока; r – расстояние до тока.
α1
 В
В
I
α2
Магнитное поле бесконечного прямого тока:
I
В r
r
В
Магнитное поле в центре кругового тока радиусом r:
В
r
I
Магнитное поле на оси соленоида конечной длины:
PDF created with pdfFactory Pro trial version www.pdffactory.com

70
где n = N/L – число витков, приходящихся на единицу длины; N, L – соответственно, общее число витков и длина соленоида; α1, α2 −
углы, под которыми из произвольной точки на оси соленоида видны его концы.
5.3. Закон Ампера. Взаимодействие параллельных токов
Сила Ампера, действующая на элемент тока I длиной dl:
r r
где α – угол между dl и В .
Направление силы Ампера определяется правилом левой руки:
если ладонь левой руки расположить так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца расположить по направлению тока, то отогнутый большой палец покажет направление силы, действующей на ток.
FA
I
В
Сила Ампера, действующая в магнитном поле на ток I конечной длины l:
Сила Ампера, действующая в однородном магнитном поле на прямолинейный ток конечной длины l:
F = IlBsin α ,
r
где α – угол между вектором плотности тока в проводнике и вектором B .
PDF created with pdfFactory Pro trial version www.pdffactory.com
