справочник по физике

здесь предполагается, что система K′ движется со скоростью υ в положительном направлении оси х системы отсчета K, причем оси х' и х совпадают, а оси у' и у, z' и z параллельны, с − скорость света в вакууме.

Из преобразований Лоренца вытекает:

где t – промежуток времени между событиями, отсчитанный покоящимися часами: t′ − промежуток времени между двумя событиями, отсчитанный движущимися со скоростью υ часами;

– релятивистское (лоренцево) сокращение длины:

=1 − υ ,

где l0 – длина стержня, измеренная в системе отсчета, относительно которой стержень покоится (собственная длина); l – длина стержня, измеренная в системе отчета, относительно которой он движется со скоростью υ;

PDF created with pdfFactory Pro trial version www.pdffactory.com

22

– релятивистский закон сложения скоростей:

где предполагается, что система K' движется со скоростью u в положительном направлении оси х системы отсчета K, причем оси х и х¢ совпадают, у' и у, z' и z параллельны.

Интервал S12 между событиями – инвариантная величина:

где tl2 - промежуток времени между событиями 1 и 2; l12 - расстояние между точками, где произошли события.

Масса релятивистской частицы:

где m0 - масса покоя.

Релятивистский импульс:

Основной закон релятивистской динамики:

Энергия покоя частицы:

PDF created with pdfFactory Pro trial version www.pdffactory.com

23

где m0 – масса покоя частицы.

Полная энергия частицы:

Кинетическая энергия частицы:

Связь между энергией и импульсом релятивистской частицы:

2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Основные формулы и определения

2.1. Основные понятия молекулярно-кинетической теории

Атом – наименьшая часть химического элемента, являющаяся носителем его свойств.

Молекула – наименьшая устойчивая частица вещества, обладающая его основными химическими свойствами и состоящая из атомов, соединенных между собой химическими связями.

Количество вещества – физическая величина, определяемая числом специфических структурных элементов – молекул, атомов или ионов, из которых состоит вещество.

PDF created with pdfFactory Pro trial version www.pdffactory.com

24

Единица количества вещества 1 моль (моль).

Молярная масса:

M = m0NA .

Постоянная Авогадро NA – число атомов, содержащихся в одном моле любого вещества; m0 – масса одной молекулы.

Единица молярной массы 1 килограмм на моль (кг/моль).

Молярный объем:

Vm = Vν .

Единица молярного объема 1 кубический метр на моль (м3/моль).

Число молей вещества:

v = mM ; v = V Vm ,

где m – масса; М – молярная масса; V – объем; Vm – молярный объем.

Масса одной молекулы:

m0 = M NA ,

где М – молярная масса; концентрация n0 определяется из соотношения:

n0 = NV .

Число молекул в данной массе вещества:

N= mm0 = m NA M .

2.2.Параметры состояния вещества

Температура Т – физическая величина, характеризующая состояние

термодинамического равновесия макроскопической системы и определяющая направление теплообмена между телами. Она является мерой средней кинетической энергии беспорядочного движения молекул.

Единица температуры 1 кельвин (К).

PDF created with pdfFactory Pro trial version www.pdffactory.com

25

Наиболее вероятное значение энергии молекул:

< В > = /2.

где i − число степеней свободы молекул (для одноатомного газа i = 3; для двухатомного газа i = 5; для многоатомного газа i = 6); k − постоянная Больцмана; T − термодинамическая температура.

Термодинамическая температура связана с температурой шкалы

Давление р – физическая величина, определяемая силой, действующей

со стороны газа на единицу площади поверхности в перпендикулярном к поверхности направлении:

p = F / S .

Единица давления 1 паскаль (Па). 1 Па = 1 Н/м2.

Нормальному атмосферному давлению соответствует 105 Па.

Объем V.

Единица объема 1 кубический метр (м3).

2.3. Законы, описывающие поведение идеальных газов

Идеальный газ – газ, собственный объем молекул которого пренебрежимо мал по сравнению с объемом сосуда, а между молекулами газа отсутствуют силы взаимодействия, за исключением парных столкновений. Вероятность тройных столкновений мала. Столкновения молекул газа между собой и со стенками сосуда считаются абсолютно упругими.

PDF created with pdfFactory Pro trial version www.pdffactory.com

26

Уравнение состояния идеального газа (уравнение МенделееваКлапейрона):

pVm = RT − для одного моля газа;

pV = mRT/M; pV = vRT − для произвольной массы газа.

Здесь Vm − молярный объем; M − молярная масса; m − масса газа; v = m/M − число молекул вещества; R − универсальная газовая постоянная; Т – термодинамическая температура.

Еще одна формула уравнения состояния, вытекающая из уравнения Менделеева-Клапейрона

p = nkT,

где р – давление; n – концентрация молекул, k – постоянная Больцмана.

Объединенный газовый закон (уравнение Клапейрона):

pV T = const ; p1V1T1 = p2 V2 T2 .

Справедлив только при ν = const.

Закон Бойля-Мариотта (изотермический процесс):

pV = const; p1V1 = p2V2 при T = const , m = const .

Кривая, изображающая зависимость между величинами р и V при постоянной температуре, называется изотермой. Изотермы представляют собой гиперболы.

р

T1 < T2 < T3

T2T3

T1

V

Изобарный процесс на диаграмме в координатах V, t изображается прямой, которая называется изобарой.

PDF created with pdfFactory Pro trial version www.pdffactory.com

27

V

p2 = const

p1 = const

V= V0 (1 + αt), или V T = const ; V1V2 = T1T2 при p = const , m = const .

Закон Шарля (изохорный процесс):

давление при 0 oC , коэффициент α =1273 K-1, p, V, T соответственно давление, объем и термодинамическая температура.

Закон Дальтона для давления смеси n идеальных газов:

PDF created with pdfFactory Pro trial version www.pdffactory.com

28

n

p = å pi , i=1

где pi - парциальное давление i-ой компоненты газа.

Парциальное давление – давление, которое оказывал бы газ, входящий в состав смеси, если бы он один занимал объем, предоставленный смеси при той же температуре.

Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы. При нормальных

условиях ( p =1,013 ×105 Па ; T = 273K ) этот объем равен

Vm = 22,41×10-3 м3/моль.

Основное уравнение молекулярно-кинетической теории газов:

PDF created with pdfFactory Pro trial version www.pdffactory.com

29

Скорости молекул:

наиболее вероятная:

υв = 2RTM ,

средняя квадратичная:

< υкв >= 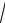3RTM ,

средняя арифметическая:

< υ >= 8RTπM ,

где Т − абсолютная температура газа; М − молярная масса газа; m0 − масса одной молекулы; R − универсальная газовая постоянная; k − постоянная Больцмана.

Барометрическая формула (зависимость атмосферного давления от высоты):

p = p0 exp[− Mg(h − h0 )RT ],

где p и p0 − давление газа на высоте h и h0 , М − молярная масса газа, m0 − масса молекулы, R − универсальная газовая постоянная, k − постоянная Больцмана.

Больцмановское распределение частиц во внешнем потенциальном

поле:

n = n0 exp[− MghRT ],

где n и n0 − концентрации молекул на высоте h и h0 = 0.

2.4. Среднее число столкновений и длина свободного пробега молекул

Среднее число соударений, испытываемых молекулой за 1 с:

<Z>= 2πd 2n < υ > ,

где d − эффективный диаметр молекулы (минимальное расстояние, на которое сближаются при столкновении центры двух молекул); n − концентрация молекул; <υ> − средняя арифметическая скорость молекул

PDF created with pdfFactory Pro trial version www.pdffactory.com

30

dо о

d

Средняя длина свободного пробега молекул газа – среднее значение расстояния, проходимого молекулой между двумя последовательными

столкновениями:

<l >= < υ >< Z > =12πd 2n .

2.5.Явление переноса в термодинамически неравновесных системах

Явление переноса – особые необратимые процессы в термодинамически неравновесных системах, в результате которых происходит пространственный перенос энергии, массы, импульса или заряда.

Теплопроводность – один из видов явлений переноса, заключающийся в том, что если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных

столкновений молекул происходит выравнивание средних кинетических энергий молекул, т.е. температур.

Закон Фурье для теплопроводности:

Q = −λ(dTdx) s t ,

где Q − количество теплоты, протекающей в направлении х через площадку s за время t ; dT dx − градиент температуры; λ − коэффициент

теплопроводности. Знак минус показывает, что энергия переносится в направлении убывания температуры.

Коэффициент теплопроводности равен при единичном градиенте температуры тепловому потоку за единицу времени через единичную площадку, нормальную к направлению потока (плотности потока):

λ = 13cV ρυl ,

где cV – удельная теплоемкость газа при постоянном объеме; ρ − плотность газа; υ − средняя скорость теплового движения молекул; l − средняя длина свободного пробега.

PDF created with pdfFactory Pro trial version www.pdffactory.com