12. Холостой ход асинхронного двигателя
Режим холостого хода асинхронного двигателя возникает при отсутствии на валу нагрузки в виде редуктора и рабочего органа. Из опыта холостого хода могут быть определены значения намагничивающего тока и мощности потерь в магнитопроводе, в подшипниках, в вентиляторе. В режиме реального холостого хода s=0,01-0,08. В режиме идеального холостого хода n2=n1, следовательно s=0 (на самом деле этот режим недостижим, даже при допущении, что трение в подшипниках не создаёт свой момент нагрузки — сам принцип работы двигателя подразумевает отставание ротора от поля статора для создания поля ротора. При s=0 поле статора не пересекает обмотки ротора и не может индуцировать в нём ток, а значит не создаётся магнитное поле ротора.)
13. Приведение вторичной обмотки трансформатора к первичной
Для упрощения анализа и расчета режимов работы трансформатора пользуются способом, при котором одна из его обмоток приводится к другой. Смысл приведения состоит в том, чтобы сделать ЭДС первичной и вторичной обмоток одинаковыми, электромагнитную связь между обмотками заменить электрической связью и получить единую электрическую схему замещения трансформатора, построить другую, более простую и наглядную векторную диаграмму. Чаще всего вторичную обмотку приводят к первичной. Для этого условно заменяют реальную вторичную обмотку некоторой фиктивной обмоткой с числом витков:
т.е. увеличивают число ее витков в k раз. Таким образом, коэффициент приведения вторичной обмотки к первичной равен коэффициенту трансформации. Все параметры приведенной обмотки обозначают со штрихами:
и т.д. В приведенной обмотке в соответствии с новым числом витков увеличиваются все ЭДС, напряжения и падения напряжения, т.е.:
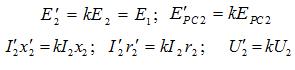
Важным условием приведения является то, чтобы мощности и потери энергии во вторичной обмотке не изменялись. Для этого должны выполняться равенства:
из которых получаются соотношения для тока и активного сопротивления приведенной вторичной обмотки:
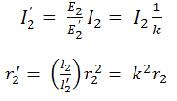
Аналогично последнему соотношению изменяются индуктивное сопротивление рассеяния приведенной вторичной обмотки и параметры нагрузки:
Для полных сопротивлений справедливы соотношения:
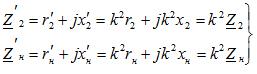
Если таким образом изменить (условно конечно) все электрические величины вторичной обмотки, то энергетические соотношения в реальном и приведенном трансформаторе сохраняются без изменений и поэтому приведение правомерно. При этом необходимо помнить, что приведение — это чисто аналитический прием, позволяющий упростить расчеты и анализ физических процессов в реальном трансформаторе.
14. Основные уравнения и векторная диаграмма трансформатора Векторная диаграмма трансформатора
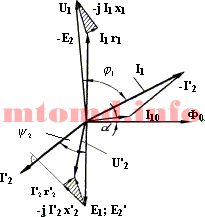
Воспользуемся вторым основным уравнением и произведем сложение векторов:
Для этого к концу вектора E2‘ пристроим вектор — j I2‘ x2‘, а к его концу — вектор — I2‘ r2‘. Результирующим вектором U2‘ будет вектор, соединяющий начало координат с концом последнего вектора. Теперь используем третье основное уравнение:
из которого видно, что вектор тока I1 состоит из геометрической суммы векторов I10 и — I2‘. Произведем это суммирование и достроим векторную диаграмму трансформатора. Теперь вернемся к первому основному уравнению:
Чтобы построить вектор — Е1 , нужно взять вектор +Е1 и направить его в противоположную сторону. Теперь можно складывать с ним и другие векторы: + j I1 x1 и I1 r1. Первый будет идти перпендикулярно току, а второй — параллельно ему. В результате получим суммарный вектор u1.
Построенная векторная диаграмма трансформатора имеет общий характер. По этой же методике можно осуществить ее построение как для различных режимов, так и для разных характеров нагрузки.