FTF 2 semestr.MARTINOV / 13

	(28)
	(29)
	(30)
	(33)
	(20)

Пусть заданы два декартовых базиса  и , связанных между собой соотношениями (28) и (29).

Рассмотрим вектор . Сам по себе он от базиса не зависит, но в базисе  он задается координатами : , а в базисе  : . При этом, естественно:

(35)

Используя (28), перейдем от базиса  к базису . Тогда

и, заменяя далее индексы в правой части , с учетом линейной независимости ортов, получим:

(36)

Аналогично для обратного преобразования

(37)

Из сравнения (36), (37) с (28), (29) следует, что координаты векторов при переходе от одного декартового базиса к другому преобразуются так же, как и орты. Поэтому векторные равенства, записанные через координаты, справдливы в любом декартовом базисе: если  и в одном базисе , то в другом базисе также имеет место . Следует отметить, что в некоторых случаях это утверждение не будет справделивым. Для примера рассмотрим вектор, который является результатом вычисления векторного произведения: . Тогда

(38)

Если  был бы истинным вектором, то это равенство должно было бы иметь такой же вид и в другом базисе

(39)

Проверим это, изменив в (38) координаты всех векторов на новые согласно (36):

(40)

Умножим обе части (40) на  и просуммируем по :

(41)

Используя соотношение ортогональности (30), получим далее

      Покажем,что

(42)

где  - определитель матрицы преобразования базисов. Действительно, умножим обе части (42) на  и просуммируем по индексам , , . Тогда в левой части с учетом (36) получим

а в правой части с учетом (20) и (33) -

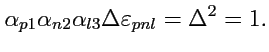
Таким образом, в отличие от (39), получаем правило преобразования координат вектора, который является результатом векторного произведения

(43)

      Значит векторное произведение ведет себя как вектор только при преобразовании базиса первого рода (), т. е. только при преобразовании правого (левого) базиса в правый (левый). При преобразовании второго рода, т. е. при переходе от правого декартового базиса к левому и наоборот, согласно (43), появляется знак минус в формуле, связывающей координаты векторов, входящих в векторное произведение. Поэтому векторное произведение не является истинным вектором и называется псевдовектором.

      Аналогично ведет себя относительно преобразования координат и смешанное произведение трех векторов, которое поэтому не является истинным скаляром и называется псевдоскаляром.