FTF 2 semestr.MAVRODI / 12
.pdf
Дифференцируемость сложной функции нескольких переменных. Первый дифференциал и инвариантность его формы.
Теорема. Пусть функции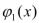 
,…,
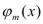дифференцируемы в точке 
=(
,…,
)
, 
=(
,…,
)
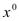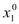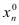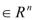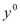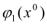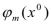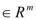и функция f(y)=f(
,…,
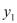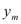) дифференцируема в точке 
.
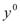Тогда сложная функция Ф(х)=f(
,…,
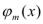) дифференцируема в точке 
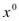, причем при х
Ф(х)-Ф( )= |
( - |
)+о( |
), |
= |
|
, i= . |
|
|
Док-во: Так как функция f(y) дифференцируема в точке |
, то найдутся функции |
, |
, |
|||||
непрерывные в точке |
=( ,…, |
) и такие, что f(y)-f( |
)= |
, |
= |
. |
||
Пользуемся, что дифференцируемая в точке функция непрерывна в этой точке, а также теоремой о
непрерывности сложной функции, получаем: |
= |
, |
непрерывны в |
||
точке , причем |
= |
= |
= |
. Подставляя в |
|
полученное |
,…, |
и используя вышеполученные соотношения, получаем: |
|||
Ф(х)-Ф(
)=
(
-
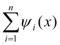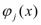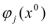). Но функции 
, 
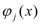, дифференцируемы в точке
,
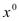поэтому найдутся такие непрерывные в точке 
функции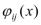 
, что:
-
=
(
-
), 
=
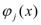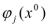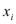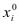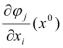, i=
,
.
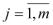Подставляя в предыдущее соотношение, получаем:
Ф(х)-Ф(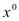
)=
(
-
), 
=
.
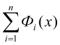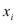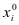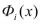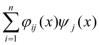Так как функции 
и 
непрерывны в точке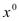 
, то и функции 
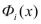непрерывны в точке 
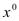. Значит, сложная функция Ф(х) дифференцируема в точке 
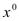, ч.т.д.
Пусть функция f(x) дифференцируема в точке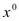 
. Тогда при 
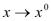ее можно записать в
виде: f(x)=f(
)+
(
)(
-
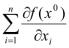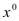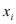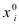)+о(
). Положим по определению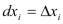 
=
-
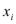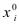. Если функция f(x) дифференцируема в точке 
, то линейную форму относительно приращений
независимых переменных |
= |
назовем первым дифференциалом функции f(x) в |
||||||
точке . Иначе можно записать как: |
|
|
|
|
|
|||
f(x)=f( )+df( )+о( |
). |
|
|
|
|
|
||
Ищем дифференциал сложной функции. Пусть функции |
,…, |
дифференцируемы в |
|
|||||
точке |
, а функция f( ,…, |
) дифференцируема в точке |
=( |
,…, |
). Тогда функция |
|||
Ф(х)=f( |
,…, |
) дифференцируема в точке , получаем: dФ( |
)=df( |
,…, |
)= |
|||
|
= |
|
|
= |
|
= |
, |
|
= |
|
. Итак, df( |
,…, |
)= |
. (*) |
|
|
|
Если бы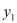 
,…,
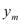были независимыми переменными, то 
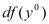отличился бы от дифференциала сложной функции (*) только тем, что в выражении 
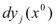- дифференциалы функции 
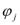, а
в 
= , 
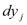- дифференциалы независимых переменных. Форма первого дифференциала инварианта относительно замены переменных. Инвариантность помогает не
задумываться о независимости переменных в варианте записи через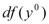 
.
Пусть функция f(x) дифференцируема во всех точках некоторого открытого множества G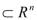
. Тогда
в каждой точке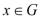 
можно вычислить дифференциал 
=
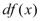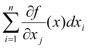. Он будет функцией 2n переменных.