FTF 2 semestr.MAVRODI / 10-11
.pdf
4. Дифференцируемость функции нескольких переменных в точке. Достаточное условие дифференцируемости функции
Опр: Функция 
определенная в окрестности 
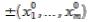называется дифференцируемой в этой точке,
если ее приращение Δf в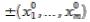 
:
=
–
=
+
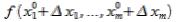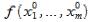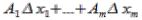, что 
Необходимое условие дифференцируемости:
Если ф-ция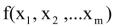 
дифференцируема в 
, то, 1.Она непрерывна в этой окрестности.
|
2.Существуют частные производные |
|
, i=1,...,m; причем |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Док-во: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если дифф.,то |
|
|
= |
+ |
|
|
+ |
|
, |
|
|
|||||
|
|
|
lim |
|
|
|
lim |
|
|
|
(при |
и |
)= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
непрерывна в |
. |
|
|
|
|
|
|
|
|
|
||||
|
Докажем, что в |
|
сущ. |
|
|
=0. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
– |
= |
+ |
|
|
, |
НО lim |
|
|
|
|||
|
=0, |
|
|
|
. Значит, lim |
|
|
=0 (аналог предела по направлению для функции m переменных) |
|
||||||||
|
|
|
|
|
– |
= |
+ |
|
|
, где |
|
|
|
||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
– |
)/ |
|
|
|
|
|
|
|
|
|
|
|
|
Тогда в пределе при |
существует |
|
что и требовалось доказать. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Достаточное условие дифференцируемости |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пусть |
|
|
|
для функции |
|
|
непрерывной в |
|
|
для функции m переменных. |
|
|||||
|
Тогда |
|
|
|
непрерывна в |
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Док-во. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказываем при m=2, (в общем случае аналогично, но более громоздко) |
|
|
|
|
|
|
|
|||||||||
|
Т.к. |
, |
непрерывна в |
, то они определены в |
=> f(x,y) определена в |
. Рассмотрим |
|||||||||||
|
∆х, ∆у такие, что |
|
принадлежит |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
– |
|
|
|
– |
+ |
|
|
||||
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
|
— дифф. по х на |
, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
– дифф. по у на |
, |
|
|
|
|
. По теореме Лагранжа: |
|
|||||
|
|
|
|
|
|
= |
+ |
|
|
|
|
|
|
|
|
||
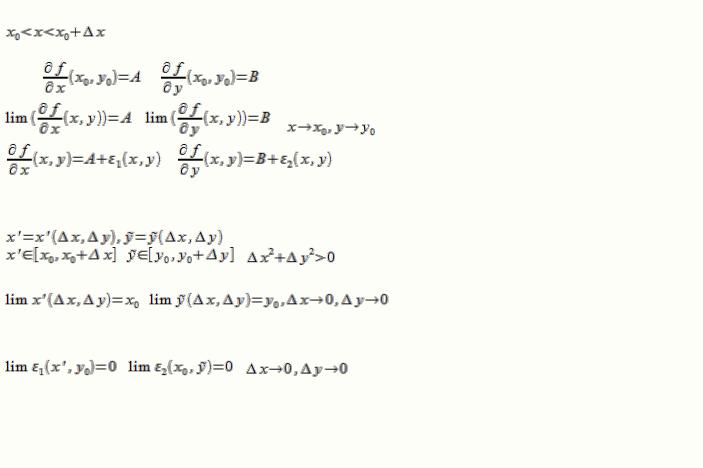
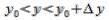(или наоборот, в зависимости от знаков ∆х,∆у)
Пусть |
и |
. В силу непрерывности соответствующих функций двух переменных: |
|
, |
; |
;
; 
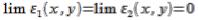, можно считать, что
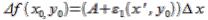+(B+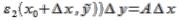
+
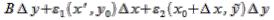
Доопределим: x'(0,0)=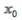
, 
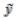(0,0)=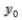
По теореме о двух ментах следует, что функции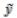 
,x' непрерывны по ∆х,∆y в 
(0,0),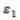 
(x,у) и 
(х,у) непрерывны по х и у в 
(0,0), по теореме о суперпозиции непрерывных функций.
.
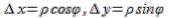
, то есть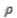 
умножается на функцию от ∆х,∆y, которая стремится к нулю, при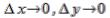 
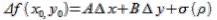. что и требовалось доказать.