FTF 2 semestr.MAVRODI / 33
.pdf
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ I РОДА: ОПРЕДЕЛЕНИЕ, ОСНОВНЫЕ СВОЙСТВА, |
||||||
ВЫЧИСЛЕНИЕ, НЕКОТОРЫЕ ПРИЛОЖЕНИЯ |
|
|
||||
Определение криволинейного интеграла I рода |
|
|
||||
Общий вид криволинейного интеграла I рода, или криволинейного интеграла по длине дуги: |
||||||
|
|
или |
; |
- двумерный случай |
|
|
ОПРЕДЕЛЕНИЕ |
|
|
|
|
||
1. |
Дугу |
кривой |
или |
в |
|
|
пространстве XOYZ разбиваем на nмалых |
|
|
||||
частей точками M0=A, M1,…,Mn=B; |
|
|
||||
обозначаем |
|
длины |
|
|
||
хорд |
|
, (Рис. 13) |
|
|
|
|
2. Вычисляем значения функции f (x,y,z) в произвольно выбираемых точках |
|
на i-той части |
||||
разбиения и умножаем их на соответствующие длины хорд li: |
, |
|
||||
3. Составляем интегральную сумму |
|
|
|
|||
и вычисляем её предел при λ → 0, где |
– это ранг разбиения. |
|
|
|||
4. Если предел интегральной суммы существует, является конечным и не зависит ни от способа |
||||||
разбиения дуги (l) на |
элементарные |
части, ни от выбора на них точек |
, то он |
|||
называетсякриволинейным интегралом I рода от функции |
|
|
||||
f (x, y, z) по линии l: |
|
|
|
|
||
Механическая трактовка криволинейного интеграла I рода |
|
|
||||
Если 
— это линейная плотность распределения материала по линии l (т.е. количество материала на единицу длины), то
— это «масса» тяжелой линии (l).
Основные свойства криволинейного интеграла I рода
Аналогичны свойствам определенных и кратных интегралов.
СВОЙСТВО 1 (ЛИНЕЙНОСТЬ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА ПО ПОДЫНТЕГРАЛЬНОЙ ФУНКЦИИ)
ГДЕ C1,С2 – ПОСТОЯННЫЕ ПО X, Y, Z.
СВОЙСТВО 2 (АДДИТИВНОСТЬ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА ПО ЛИНИИ ИНТЕГРИРОВАНИЯ)
Если (l)=(l1)
(l2), то
СВОЙСТВО 3 (ЗНАЧЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА ОТ ФУНКЦИИ, ТОЖДЕСТВЕННО РАВНОЙ ЕДИНИЦЕ НА ЛИНИИ ИНТЕГРИРОВАНИЯ)
Если |
на (АВ), то |
— длина дуги линии (АВ). |
СВОЙСТВО 4 (ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА I РОДА)
Если функция 
является непрерывной для 
, то 
существует.
Вычисление криволинейного интеграла I рода (Как вычисляется криволинейный интеграл I рода)
Если записать параметрические уравнения линии (l): |
, |
в которых функции 
, 
, 
являются дифференцируемыми, то можно показать, что дифференциал длины дуги dl пересчитывается по формуле, аналогичной формуле для дифференциала длины дуги плоской линии (см. тему «Интегральное исчисление функции одной переменной»):
,
а криволинейный интеграл I рода сводится к определенному интегралу по переменной 
.
В результате получается следующая формула для вычисления криволинейного интеграла I рода:
(2)
При этом в качестве параметра t на линии (l) можно брать любую независимую переменную.
В частности, если дан двумерный криволинейный интеграл и линия интеграирования l является графиком функции 
, 
, то в качестве параметра можно взять независимую
переменную x: тогда 
и формула сведения криволинейного интеграла I рода к определенному интегралу будет иметь вид:
(3)
.
Если плоская линия l задана уравнением |
, |
в полярной системе координат, то в |
||
качестве параметра нужно брать полярный угол |
|
и использовать связь между полярными |
и |
|
декартовыми |
координатами: |
|
, |
. |
Тогда
формула сведения крволинейного интеграла I рода к определенному интегралу в полярных координатах:
(4)
При составлении формул (2)-(4) нужно учитывать, что значение криволинейного интеграла I рода не зависит от направления на линии интегрирования l, поэтому 
всегда в следствие этого пределы интегрирования по независимой переменной «от 
до 
» всегда такие, что 
<
.
Пример 1 (вычисление криволинейного интеграла I рода)
Вычислить 
, где (l)— это отрезок прямой, соединяющий точки А(1; 2; 3) и В(-4; 8; 4).
Решение
Составляем параметрические уравнения прямой в пространстве по двум её известным точкам:
Находим пределы изменения для t на отрезке AB: tA=0, tB=1 
Сводим искомый криволинейный интеграл к определенному интегралу по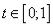 
, используя формулу (2), в которой 
:
.
2. Вычислить 
, где l – это часть координаты 
, 
.
Решение
;
;
,
так как 
при 
;
.