FTF 2 semestr.MAVRODI / 47
.pdf
Интегральный признак
Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда.
Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимостинесобственного интеграла соответствующей функции на 
, последний часто может быть найден в явном виде.
Формулировка теоремы
Пусть для функции f(x) выполняется: |
|
|
1. |
(функция принимает неотрицательные значения) |
|
2. |
|
(функция монотонно убывает) |
3. |
(соответствие функции ряду) |
|
Тогда ряд |
и несобственный интеграл |
сходятся или расходятся одновременно. |
|
|
|
Набросок доказательства
1.Построим на графике f(x) ступенчатые фигуры как показано на рисунке
2.Площадь большей фигуры равна 
3.Площадь меньшей фигуры равна 
4.Площадь криволинейной трапеции под графиком функции равна
5.Получаем
6.Далее доказывается с помощью критерия сходимости знакоположительных рядов.
Примеры
|
расходится так как |
. |
|
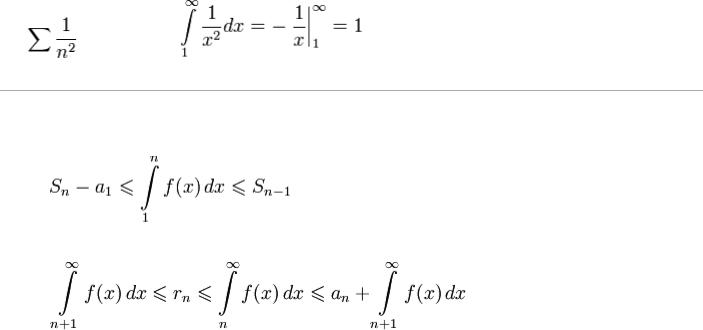
сходится так как |
. |
Оценка остатка ряда
Интегральный признак Коши позволяет оценить остаток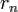 
знакоположительного ряда. Из полученного в доказательстве выражения
с помощью несложных преобразований получаем:
.