FTF 2 semestr.MAVRODI / 46

Свойства сходящихся числовых рядов.

1.Если сходится числовой ряд , то сходящимся будет и ряд . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

2.Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд , причем 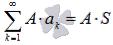, где A – произвольная постоянная.

3. Если сходятся числовые ряды и , их суммы равны A и Bсоответственно, то сходящимися будут

ряды 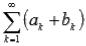и 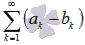, причем их суммы будут равны A + B и A - B соответственно.

Пример.

Докажите сходимость числового ряда .

Решение.

Запишем ряд в другом виде . Числовой

ряд 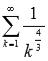сходится, так как обобщенно гармонический

ряд является сходящимся при s > 1, а в силу второго свойства сходящихся числовых рядов будет сходится и ряд с числовым

коэффициентом .