FTF 1 semestr.MAVRODI / 33

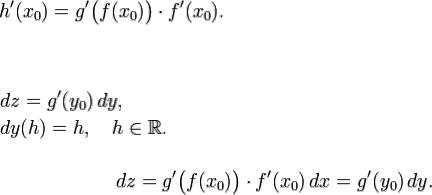
Правила дифференцирования

6) Если функция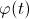 имеет производную в точке, а функцияимеет производную в точке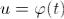, то сложная функция 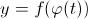имеет производную в точке , причем 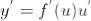(правило дифференцирования сложной функции).

Инвариантность формы первого дифференциала

Дифференциал функции 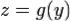в точке 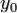имеет вид:

где 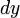— дифференциал тождественного отображения :

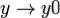Пусть теперь 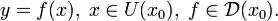Тогда 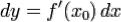, и согласно

цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того,

является ли переменная функцией или нет.

7) Пусть функция y = f(x) имеет производную в точке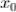, причем . Если существует обратная функция 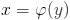, то она имеет производную в точке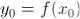

и (производная обратной функции).