
ИКТСС_2у_1 / Лекции / Теория электрических цепей-Лк3-ИКТиСС-2у-1-Панин
.pdf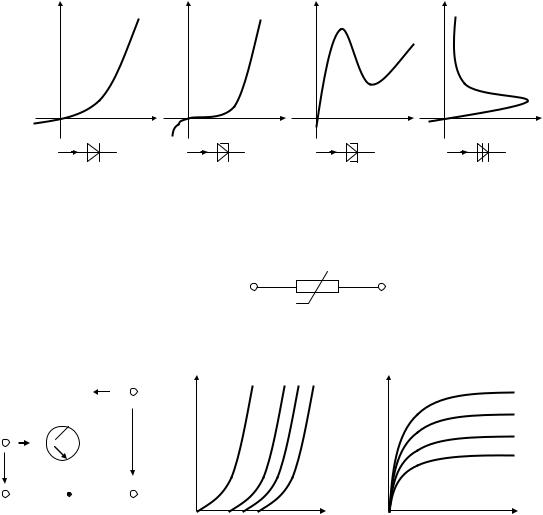
Лекция № 3 Нелинейные электрические цепи в стационарном режиме
Нелинейные резистивные элементы Нелинейными резистивными элементами (диодами) являются все полупроводниковые и
электронные двухполюсные безинерционные приборы. Единственной их характеристикой является зависимость мгновенного значения тока от приложенного мгновенного значения напряжения (ВАХ).
i |
i |
i |
i |
u |
u |
u |
u |
выпрямительный диод |
стабилитрон |
туннельный диод |
динистор |
Для удобства двухполюсные нелинейные резистивные элементы будем называть нелинейными резисторами.
Обозначение:
Рассмотрим нелинейные резистивные четырехполюсники (транзисторы, электронные лампы)
|
|
|
|
|
i2 |
|
i1 |
u2 = 0 u2 > 0 |
i2 |
iБ4 |
|
|
|
|
|
K |
|
|
|
|
|
|
|
i1 |
|
|
|
|
|
|
iБ3 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
iБ2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
u2 |
|
|
|
|
u1 |
|
|
|
Э |
|
|
|
iБ1 |
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
биполярный транзистор |
0 |
u1 |
0 |
u2 |
||||||
с общим эмиттером |
|
|||||||||
|
входная характеристика |
выходная характеристика |
||||||||
|
|
|
|
|
|
|
||||
При анализе транзисторов используется система уравнений вида:
u f i ,u . i f i ,u
Для нелинейных резисторов важным параметром является сопротивление (проводимость).
Существуют два вида сопротивления (проводимости).
Статическое сопротивление (статическая проводимость) – определяется отношением постоянного
напряжения (тока) к постоянному току (напряжению): Rст |
|
U |
, Gст |
I |
. |
|
I |
U |
|||||
|
|
|
|
Дифференциальное сопротивление (дифференциальная проводимость) – отношение приращения напряжения (тока) к приращению тока (напряжения).
Rдиф |
|
u |
|
, Gдиф |
|
i |
. |
|||||
|
|
|
|
|
|
|||||||
|
|
i |
|
|
|
|
u |
|||||
Обычно переходят к пределу этих отношений: |
|
|
|
|
|
|
|
|
||||
Rдиф |
du |
, Gдиф |
di |
. |
||||||||
|
|
|
||||||||||
|
|
di |
|
|
|
|
du |
|||||
Иногда используют понятие крутизна: |
|
|
|
|
|
|
|
|
|
|
|
|
S Gдиф |
|
|
di |
. |
||||||||
Rдиф |
|
|||||||||||
|
|
|
|
|
|
du |
||||||
Например: нелинейный резистор имеет ВАХ вида: i u a a u a u .
Определить статическое и дифференциальное сопротивление в точке u U .
1. Определяем значение тока, если u U : I a a U a U .
2. |
Определяем статическое сопротивление: Rст |
U |
|
|
|
|
|
|
U |
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
I |
|
a a U a U |
|
|||||||||
3. |
Определяем дифференциальную проводимость: Gдиф |
di |
|
|
|
|
|
a a U . |
||||||
|
|
|
|
|
||||||||||
du |
u U |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
4. |
Определяем дифференциальное сопротивление: Rдиф |
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
a a U |
|||||||||
|
|
|
|
|
Gдиф |
|
||||||||
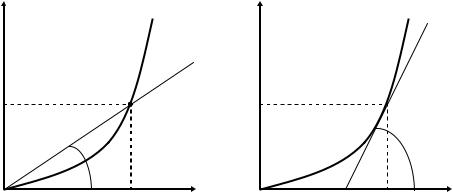
Данный способ является аналитическим. Рассмотрим графический способ определения статического и дифференциального сопротивления.
i |
i |
I0 |
|
|
A |
I0 |
|
|
|
|
|
|
|
|
A |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
U0 |
u |
0 |
|
|
|
|
|
|
u |
|||
|
|
|
|
|
|
|
|
U1 U0 |
|||||||
|
|
Gст |
I |
|
tg , Rст |
|
U |
|
|
ctg . |
|||||
|
|
U |
|
I |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Gдиф |
i |
|
I |
tg , Rдиф |
|
|
u |
|
U U |
ctg . |
|||||
|
U U |
|
|
|
|||||||||||
|
u |
|
|
|
|
|
i |
|
|
I |
|||||
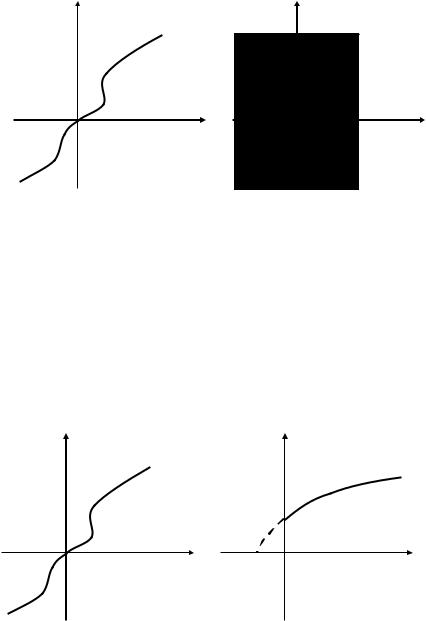
Нелинейные реактивные элементы К нелинейным реактивным элементам относят:
Нелинейные индуктивные элементы – катушки с ферромагнитными сердечниками.
Нелинейность обусловлена характеристикой намагниченности материала сердечника B H .
Поскольку Ф BS, а H iw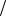 L, где S – сечение, L – длина сердечника, то вид зависимости предопределяет характер вебер-амперной характеристики Ψ i , где Ψ Фw .
L, где S – сечение, L – длина сердечника, то вид зависимости предопределяет характер вебер-амперной характеристики Ψ i , где Ψ Фw .
Представим вебер-амперные характеристики:
Ψ |
Ψ |
i |
i |
Нелинейный индуктивный элемент характеризуется:
Статической индуктивностью Lст |
|
Ψ |
, дифференциальной индуктивностью Lдиф |
|
dΨ |
. |
|
||||||
|
|
|||||
|
|
I |
|
di |
||
Нелинейных емкостных элементов различают две группы: а) вариконды, нелинейность которых связана с зависимостью диэлектрической проницаемости ε от напряженности электрического поля E, б) варикапы – полупроводниковые диоды, нелинейная емкость которых определяется свойствами p-n-перехода.
Описываются вольт-кулонной характеристикой.
q |
q |
u |
u |
Нелинейный элемент емкости характеризуется статической и дифференциальной емкостью:
Cст |
q |
, Cдиф |
dq |
. |
u |
|
|||
|
|
du |
||
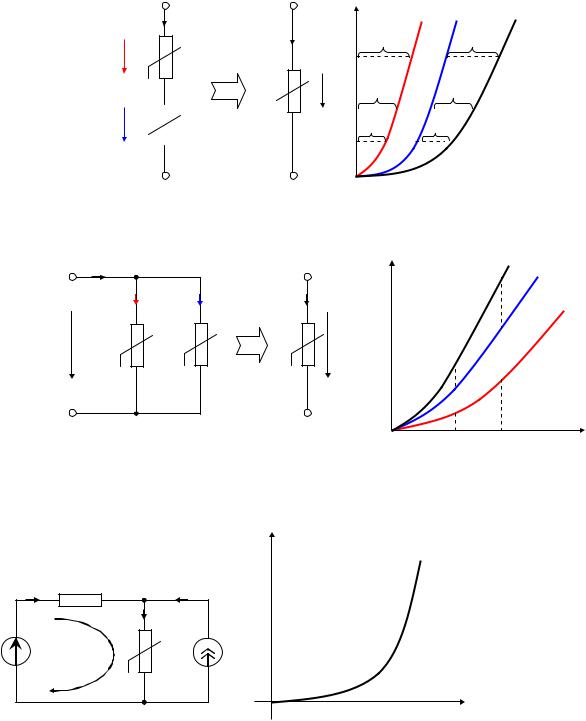
Методы расчета нелинейных резистивных электрических цепей Графо-аналитический метод расчета НЭ Рассмотрим последовательное соединение нелинейных резистивных элементов:
|
i |
i |
|
i |
|
u1 |
|
|
HЭ1 |
|
|
|
|
|
|
|
u |
u2 |
|
|
HЭ |
|
|
|
|||
|
|
|||
|
|
|
HЭ2 |
|
|
|
|
||
 u
u
На основании II закона Кирхгофа: u u u получаем ВАХ НЭ.
Рассмотрим параллельное соединение нелинейных резистивных элементов.
i
|
|
i |
i1 |
i2 |
i |
НЭ1 |
НЭ2 |
НЭ |
u |
|
u |
u
На основании I закона Кирхгофа: i i i получаем ВАХ НЭ.
Аналитический метод расчета НЭ основан на законах Кирхгофа.
i
I |
R |
J |
|
, |
U |
нэ |
|
|
|
|
|
|
|||||||
|
|
I |
|
|
|
|
|
. |
|
|
|
I |
Iнэ |
|
, |
U |
|
||
|
|
нэ |
U |
нэ |
|
||||
|
I |
|
нэ |
|
нэ |
|
|
|
|
E |
НЭ |
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
u |
На основании законов Кирхгофа запишем уравнение:
Iнэ I J, E Uнэ IR .
Находим решение, если Uнэ :
I Iнэ J, E Uнэ Uнэ J R .
После преобразований получим:
R Uнэ Uнэ JR E .

Uнэ |
|
|
|
|
JR E |
– первое решение. |
R |
R |
|
||||
|
|
|
R |
|||
Находим решение, если Uнэ :
I J , Uнэ E JR – второе решение.
Второе решение противоречит условию Uнэ , поэтому оставляем первое решение.
Если ВАХ НЭ описывалась более сложной функцией, то аналитическое решение получить было бы крайне сложно.
Аналитическое представление ВАХ Точное представление ВАХ в аналитическом виде крайне сложно, поэтому на первое место выходит приближенное представление ВАХ (задача аппроксимации).
Задача аппроксимации состоит в двух этапах:
1.Выбор аппроксимирующей функции f x
2.Выбор критерия оценки «близости» Λ в интервале аппроксимации a x b .
Λmax f x x – линейный критерий близости,
|
|
b |
Λ |
f x x dx – квадратичный критерий близости, |
b a a
где x – аппроксимируемая функция.
Виды аппроксимации Полиномиальная (степенная) аппроксимация
В качестве аппроксимирующей функции используется алгебраический полином:
f x a a x a x an xn .
Добиваются совпадения значений аппроксимирующей и аппроксимируемой функций в возможно большем числе выбранных точек в интервале a x b . Соответствующий метод приближения называется интерполяция. Выбранные точки – узлы интерполирования их число на единицу превышает степень интерполирующего полинома, т.е. Nуз.инт. n .
Из условия f xk xk , k , , , ,n получим n систему линейных уравнений:
a a x a x an xn x a a x a x an xn x
a a xn a xn an xnn xn
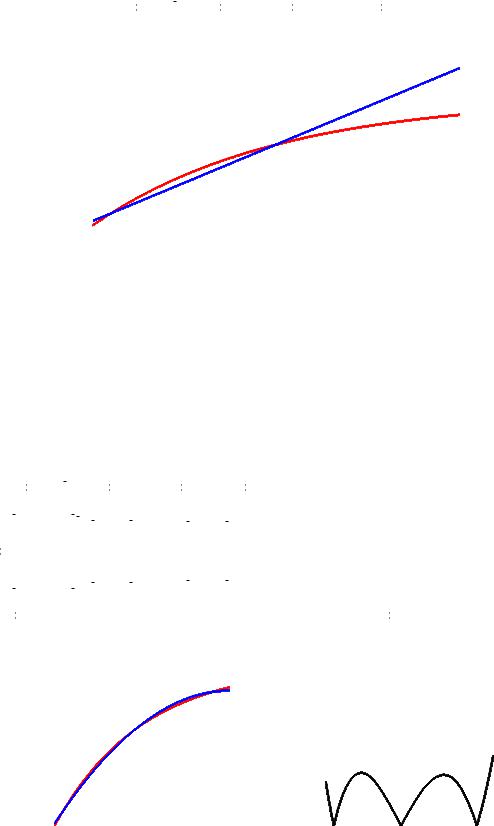
Пример: интерполируем полиномом f x a a x в интервале x функцию x e x .
1.Определяем число узлов интерполирования: Nуз.инт. n .
2.Выбираем значение узлов интерполяции: x . , x .
3.Получим систему линейных уравнений:
|
|
a a . e . |
, откуда a . , a . . |
|
|||||||||||||||||||||||||||||||
|
|
a a e |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1.5 |
|
(x) |
|
1 |
|
|
e x |
|
a0 |
|
0.036 |
|
a1 |
|
0.597 |
|
f(x) |
|
|
a0 |
|
|
|
a1 x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(x) 0.9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.2 |
0.4 |
0.6 |
|
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
||||||||||||||||||||||||
0 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Аппроксимирующий полином имеет вид: f x . . x. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Наибольшее отклонение наблюдаем в точке x , а именно: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Λ max |
|
f x x |
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
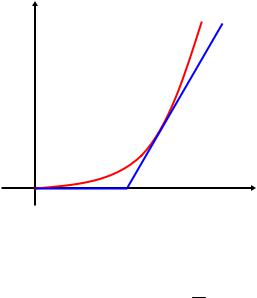
Точность аппроксимации увеличивается при увеличении степени полинома: |
|
||||||||||||||||||||||||||||||||||
Пример: интерполируем |
полиномом |
|
f x a a x a x в |
|
|
интервале x функцию |
|||||||||||||||||||||||||||||
x e x . Число узлов интерполяции: 3.
|
(x) |
|
|
|
1 |
|
|
|
|
|
e x |
|
1 |
|
x0 |
|
0.1 |
|
|
x1 |
|
|
0.9 |
|
x2 |
|
1.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
x0 |
|
|
|
2 |
|
|
(x0) |
|
|
|
|
|
0.014 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
a |
|
|
|
1 |
|
|
x1 |
|
x12 |
|
|
|
|
|
|
(x1) |
|
|
|
a |
|
0.832 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(x2) |
|
|
|
|
|
|
|
0.209 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
x2 |
|
x2 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f(x) |
|
|
a |
|
|
|
|
|
|
|
a |
x |
|
|
|
|
a |
|
|
|
a |
|
|
0.014 |
|
|
|
|
a |
|
0.832 |
|
a |
|
|
|
0.209 |
(x) |
|
|
|
f(x) |
|
(x) |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.038 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(x) |
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x) |
0.025 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f(x) |
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.013 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0.5 |
|
|
|
1 |
|
1.5 |
|
|
2 |
|
|
|
|
|
|
|
0.5 |
|
|
1 |
1.5 |
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
Кусочно-линейная аппроксимация заключается в замене реальной ВАХ приближенной, состоящей
из отрезков прямых линий, выбираемых касательными.
i
,приu U |
|
||
i u S u U |
|
,приu U |
|
|
|
||
0 |
U0 |
u |
Аппроксимация трансцендентными функциями (экспоненты, гиперболические и другие функции).
i u A e u , i u A th u B , где A,B, – варьируемые параметры.
Контрольные вопросы
1.Приведите примеры нелинейных резистивных элементов. Как они обозначаются?
2.Что называется вольтамперной характеристикой (ВАХ)?
3.Что такое статическое и дифференциальное сопротивление? Как они определяются графически по ВАХ?
4.Какова причина проявления нелинейности индуктивного элемента?
5.Какова причина проявления нелинейности ёмкостного элемента (варикапа)?
6.Какова причина проявления нелинейности ёмкостного элемента (вариконда)?
7.Какие методы расчета нелинейных резистивных электрических цепей Вы знаете?
8.Что Вы понимаете под аппроксимацией ВАХ?
9.Какие виды аппроксимации ВАХ Вы знаете?
10.От чего зависит точность при полиномиальной аппроксимации?
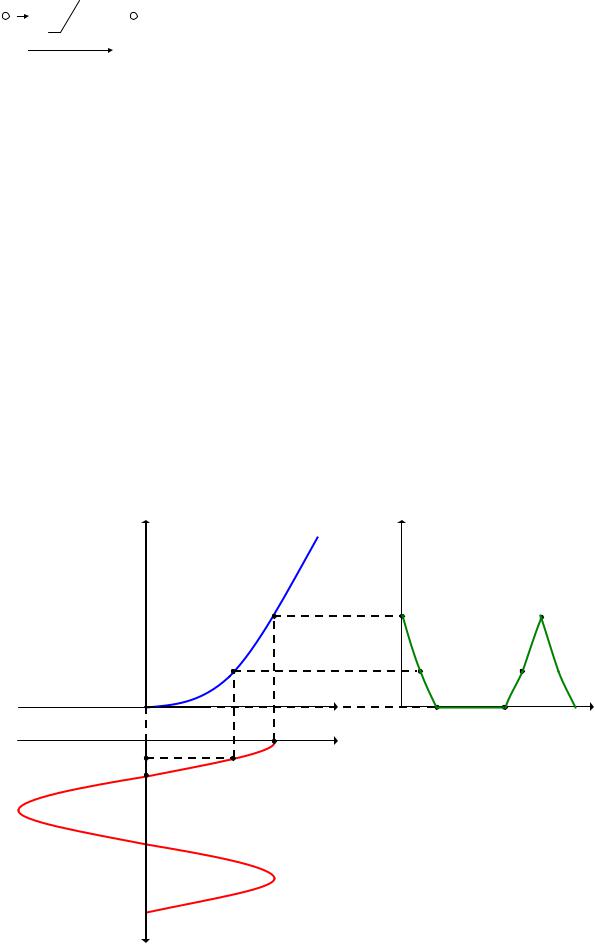
Спектральные методы анализа нелинейных электрических цепей при гармоническом воздействии
i(t) |
|
|
Пусть на вход нелинейной резистивной цепи, описываемой ВАХ |
|
НЭ |
i(u), действует гармоническое напряжение: |
|
|
|||
|
|
|
|
u(t) Um cos t .
u(t) Требуется определить спектр отклика, т.е. спектр тока i(t).
Классический метод анализа заключается прямой подстановкой u(t) в i(u), но эта процедура является весьма громоздкой и сложной. Существуют следующие часто применяемые методы определения спектрального состава тока.
метод тригонометрических функций кратного аргумента
метод угла отсечки
метод трех и пяти ординат
Метод тригонометрических функций кратного аргумента
Этот метод применим в случае полиномиальной аппроксимации ВАХ. Рассмотрим
воздействие на нелинейный резистивный элемент, ВАХ которого аппроксимирована полиномом:
i u a a u a u ... an un ,
гармонического колебания u(t) Um cos t. Применяем графо-аналитический метод. Видно, что реакция тока является негармонической периодической функцией времени. Спектр тока содержит несколько гармоник (ряд Фурье), которые подлежат определению.
i(u) i(t)
Imax
u |
0 |
to |
t |
0
Um u(t)
to
t

Осуществляя прямую подстановку, получаем:
i u a0 a1 Um cos t a2 Um2 |
cos2 t ... an Umn cosn t. (пусть n 5) |
||||||||
Понизим порядок данного полинома через тригонометрические функции кратных |
|||||||||
аргументов, полагая t. Т.к. cos |
cos |
|
, то |
|
|
||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
||||||
cos cos |
|
|
|
|
|
|
cos |
|
cos cos . |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
Учитывая, что cosacosb cos a b cos a b 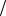 имеем:
имеем:
cos cos cos cos cos cos .
|
|
|
|
По аналогии можно получить:
cos cos cos , cos cos cos cos .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для тока выражение приобретает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|||||||||||
|
|
i a a Um cos a Um |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
a Um |
|
|
|
|
|
cos |
|
|
|
|
cos |
a Um |
|
|
|
|
|
|
|
|
|
cos |
|
cos |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
a Um |
|
|
|
|
cos |
|
|
|
|
|
cos |
|
|
|
|
cos . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Приводим подобные слагаемые: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
i a |
|
|
|
|
|
a |
Um |
|
|
|
a Um |
a Um |
|
|
|
a Um |
|
|
|
a |
Um cos |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
a |
Um |
|
|
|
a Um cos |
|
|
|
a |
Um |
|
|
|
|
a Um cos |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a |
Um |
cos |
|
|
|
a Um cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Спектральный состав тока можно записать в виде:
i I I cos I cos I cos I cos I cos ,
где амплитуды гармоник определяются как:
|
|
I |
|
a |
|
|
|
|
a |
|
U |
|
|
|
a |
|
U |
|
, I a |
|
U |
|
|
|
a |
|
|
U |
|
|
|
a |
|
U |
, |
||||||||
|
|
|
|
m |
|
|
|
m |
|
m |
|
|
m |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
||||||||||||||||||||||
I |
|
a Um |
|
|
a Um , I |
|
a Um |
|
|
a Um , I |
|
|
a |
Um , I |
|
a Um . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Спектр тока является дискретным, постоянная составляющая и амплитуды четных гармоник определяются только четными степенями полинома. Появление гармоник в составе тока в элементе обусловлено нелинейностью его ВАХ, в связи с чем их часто называют продуктами нелинейности. Изобразим спектр тока:
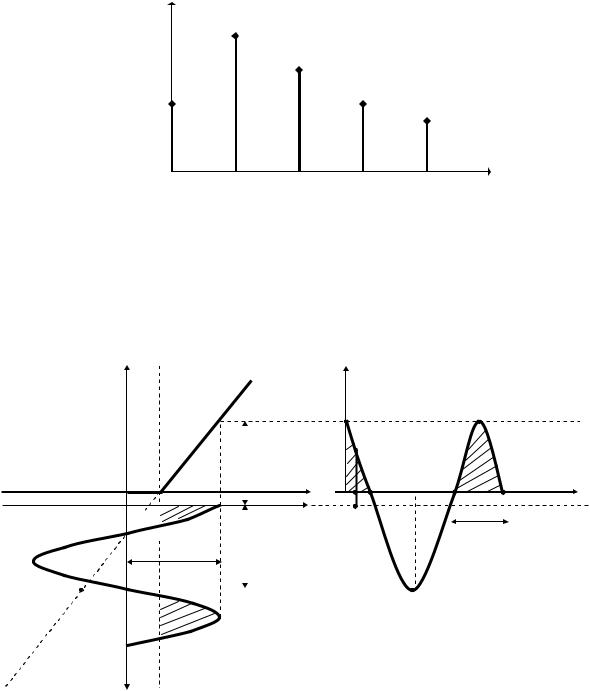
I1
I2
I0 I3
I4
0 2 3 4
Данный метод применяется воздействие вида u t Um cos t
кусочно-линейной функцией.
i
0 U0

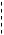
Um
t
Метод угла отсечки при кусочно-линейной аппроксимации ВАХ. Рассмотрим
на нелинейный элемент, ВАХ которого аппроксимирована
i
I |
K |
|
|
|
|
|
t |
||
u |
M u N
2
I
Применяя метод проекций, удобно сначала, определить ток, которой бы получился в случае линейной характеристики прибора с крутизной S. Поскольку нелинейный элемент работает с отсечкой, то только заштрихованная часть напряжения участвует в создании тока. Получившиеся импульсы характеризуются следующими величинами:
Угол отсечки – часть периода, в течении которого ток изменяется от максимального до нулевого значения. Максимальное значение тока – Imax.
В интервале t ток отличен от нуля и принимает следующее значение: i t KN MN Icos t Icos I cos t cos .
Максимальное значение тока наблюдается в точке 0, т.е.
Imax I cos SUm cos .
Периодическая последовательность импульсов i(t) представляется в виде ряда Фурье:
