
Blatov_lek
.pdf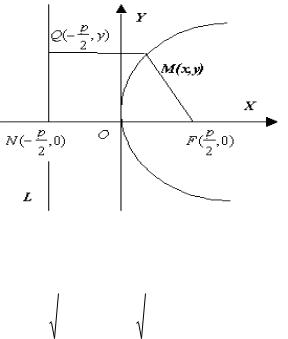
Определение Парабола - геометрическое место точек, для каждой из которых расстояние от некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой (директриса не проходит через фокус).
Выберем систему координат так, чтобы ось абсцисс проходила через точку фокуса F перпендикулярно директрисе L , начало координат расположим в середине отрезка FN . Расстояние между фокусом F и директрисой L обозначим p .
Значение p называют параметром параболы.
Пусть M x, y - |
текущая |
|
точка параболы, тогда, по |
||||||||||||
определению параболы имеем |
|
|
|
|
|
|
|
|
|||||||
QM |
FM |
|
|
|
|
||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
p 2 |
|
p 2 |
|
2 |
|
|||||||
|
x |
|
|
x |
|
|
y |
|
, |
||||||
|
|
|
|||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
||||||
отсюда получаем
y2 2 px
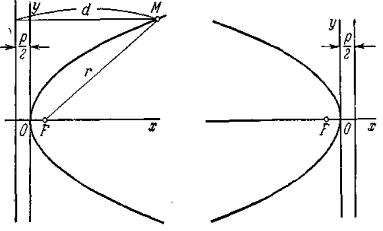
Уравнение называют каноническим уравнением параболы.
Вершина параболы находится в начале координат, и кривая симметрична относительно оси Ох.
141
|
|
|
|
|
|
|
|
x |
p |
|
- фокальный радиус точки P x, y , |
|
|||||
r |
|
|
FP |
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
|
|
||||||||||||||
|
|
|
|
x |
p |
|
|
||||||||||
q |
|
|
NP |
|
- расстояние от точки P |
до |
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
||||||||||||||
директрисы. |
|
|
|||||||||||||||
Свойства параболы |
|
|
|||||||||||||||
1. Парабола имеет ось симметрии (ось параболы). |
Точка |
||||||||||||||||
пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ox , а вершиной – начало координат.
2. Вся парабола расположена в правой полуплоскости плоскости Oxy .
При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
142
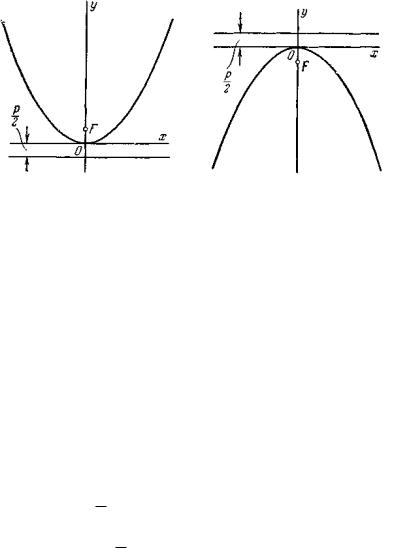
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости, то еѐ уравнение будет иметь вид
y2 2 px .
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
x2 2 py ,
если она лежит в верхней полуплоскости, и x2 2 py
— если в нижней полуплоскости.
Каждое из уравнений параболы называется каноническим.
Замечание Если для эллипса и гиперболы обозначим через r расстояние от текущей точки кривой до какого-либо фокуса, а через d - расстояние от этой точки до односторонней с этим фокусом директрисы, то оказывается, что
dr e (эксцентриситет кривой).
Для параболы же dr 1, что следует из ее определения.
Таким образом, для рассмотренных кривых второго порядка эллипса, гиперболы, параболы имеет место фокальнодиректориальное свойство: отношение расстояния текущей точки кривой до фокуса к расстоянию до односторонней с этим фокусом директрисы равно эксцентриситету кривой, т.е.
143
|
|
1, |
эллипс |
|
|
r |
|
|
|
e |
|
1, парабола . |
||
d |
||||
|
|
г ипербола |
||
|
|
1 |
||
Канонические уравнения эллипса, гиперболы, параболы получены при специальном выборе начала координат и направления осей координат, поэтому они просты и удобны для анализа.
 Пример Определить координаты фокуса и уравнение директрисы параболы y x2 .
Пример Определить координаты фокуса и уравнение директрисы параболы y x2 .
Решение
Если поменять ролями оси Ox и Oy , то каноническое уравнение параболы примет вид: x2 2 px .
Сравнивая это уравнение с заданным, получим 2 p 1, отсюда p 1 2 .
2 .
Следовательно, фокус параболы имеет координаты 0,1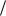 4 , а уравнение директрисы есть y 1 4
4 , а уравнение директрисы есть y 1 4
Контрольные вопросы по теме «Кривые второго порядка»
1.Дать определение окружности, эллипса.
2.Напишите канонические уравнения окружности, эллипса и объясните смысл величин, входящих в эти уравнения.
3.Что характеризует эксцентриситет эллипса?
4.Написать уравнения директрис эллипса, объяснить смысл величин в этих уравнениях, показать расположение директрис и эллипса на чертеже
5.Дать определения гиперболы, параболы.
6.Напишите канонические уравнения гиперболы и параболы, объясните смысл величин, входящих в эти уравнения.
7.Напишите уравнения директрис, асимптот гиперболы, покажите на чертеже их расположение относительно гиперболы.
144

8.Чему равен эксцентриситет параболы? Покажите на чертеже расположение директрисы относительно параболы.
Задачи для самостоятельного изучения
1. Составить уравнение окружности в каждом из следующих случаев:
а) окружность проходит через точку A 2;6 , и ее центр совпадает с точкой C 1;2 ;
б) точки A 3;2 и B 1;6 являются концами одного из
диаметров окружности; в) центр окружности совпадает с началом координат, и
прямая 3x 4y 20 0 является касательной к окружности;
г) центр окружности совпадает с точкой C 1; 2 , и прямая 5x 12y 9 0 является касательной к окружности.
2.Написать уравнение окружностей радиуса R 
 5 , касающихся прямой x 2y 1 0 в точке M 3;1 .
5 , касающихся прямой x 2y 1 0 в точке M 3;1 .
3.Какие из нижеприводимых уравнений определяют окружности? Найти центр С и радиус R каждой из них:
а) x 5 2 y 2 2 25 , б) x 2 2 y2 64 ,
в) x 5 2 y 2 2 0 , г) x2 y2 2x 4y 14 0 .
4.Определить, при каких значениях углового коэффициента k прямая y kx
а)пересекает окружность x2 y2 10x 16 0 ;
б)касается этой окружности; в) проходит вне этой окружности
5. Вычислить расстояние от центра окружности x2 y2 2x до прямой, проходящей через точки пересечения двух окружностей:
x2 y2 5x 8y 1 0 , x2 y2 3x 7 y 25 0 .
145
6.Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, кроме того, что:
а) расстояние между его фокусами 2c 6 и эксцентриситет
53 ;
б) его большая ось равна 20, а эксцентриситет 53 ;
в) его малая ось равна 10, а эксцентриситет 1213 ;
г) расстояние между его директрисами равно 5 и расстояние между фокусами равно 4.
7. Дан эллипс 9x2 25y2 225 . Найти:
а) его полуоси; б)фокусы; в)эксцентриситет; г) уравнения директрис.
8. Через |
фокус |
эллипса |
x2 |
|
y2 |
1 |
проведен |
|
|
||||||
|
|
|
25 |
15 |
|
|
|
перпендикуляр к его большой оси. Определить расстояние от точек пересечения этого перпендикуляра с эллипсом до фокусов.
9.Составить уравнение эллипса, если известны его эксцентриситет 12 , фокус F( 4,1) и уравнение
соответствующей директрисы y 3 0 .
10. Точка A( 1,5) |
лежит |
на эллипсе, |
фокус которого |
||
F( 1; 4) F, |
а |
соответствующая |
директриса |
дана |
|
уравнением |
x 2 0 . |
Составить |
уравнение |
этого |
|
эллипса. |
|
|
|
|
|
11.Точка M1(3; 1) является концом малой оси эллипса, фокусы которого лежат на прямой y 6 0 . Составить
146
уравнение этого эллипса, зная его эксцентриситет
22 .
12. Найти точки пересечения прямой x 2y 7 0 и эллипса x2 4y2 25 .
13.Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметричны относительно начала координат, зная, кроме этого, что:
а) расстояние между фокусами 2c 6 и эксцентриситет
32 ;
б) ось 2a 16 |
и эксцентриситет |
5 |
|
; |
|||
4 |
|
||||||
|
|
|
|
|
|
||
в) уравнение |
асимптот y |
4 |
x и |
расстояние между |
|||
3 |
|||||||
|
|
|
|
|
|
||
фокусами 2c 20 ; |
|
|
|
|
|
||
г) расстояние между директрисами равно 22 |
2 |
и расстояние |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
||
между фокусами 2c 26 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
на гиперболе |
x2 |
|
y2 |
1. |
|||||||||
14. Дана |
точка M |
(10; 5) |
|||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
80 |
20 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Составить уравнения прямых, на которых лежат |
|||||||||||||||||||
фокальные радиусы точки М1. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
5; |
9 |
|
|
|
|
|
|
||||
15. Убедившись, что точка M1 |
|
лежит на гиперболе |
|||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
|
x2 |
|
y2 |
1, определить фокальные радиусы точки M |
|
. |
|||||||||||||
16 |
9 |
1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16. Эксцентриситет гиперболы |
2 , центр еѐ |
лежит в |
|||||||||||||||||
начале координат, один из фокусов F(12;0) . Вычислить расстояние от точки M1 гиперболы с абсциссой, равной 13, до директрисы, соответствующей данному фокусу.
147

17. Определить точки гиперболы |
x2 |
|
y2 |
1 , расстояние |
|
|
|||
|
64 |
36 |
|
|
которых до правого фокуса равно 4,5.
18.Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты еѐ центра С, полуоси, эксцентриситет, уравнения асимптот и директрис:
а)16x2 9y2 64x 54y 161 0 ; б) 9x2 16y2 90x 32y 367 0 .
19.Составить уравнение параболы, вершина которой находится в начале координат, зная что:
а) парабола расположена в правой полуплоскости симметрично относительно оси Ox , и еѐ параметр p 3 ;
б) парабола расположена в левой полуплоскости симметрично относительно оси Ox , и еѐ параметр p 0.5 ; в) парабола расположена в верхней полуплоскости
симметрично относительно оси Oy , и еѐ параметр p 14 ;
г) парабола расположена в нижней полуплоскости симметрично относительно оси Oy , и еѐ параметр p 3 .
20. |
Найти фокус |
F и уравнение директрисы |
параболы |
||
|
y2 24x . |
|
|
|
|
21. |
На параболе |
y2 16x |
найти точки, фокальный радиус |
||
|
которых равен 13. |
|
|
|
|
22. |
Составить уравнение |
параболы, если даны |
еѐ фокус |
||
|
F(7;2) и директриса x 5 0 . |
|
|||
23. |
Определить |
точки |
пересечения |
прямой |
|
|
3x 4y 12 0 и параболы |
y2 9x . |
|
||
24.В следующих случаях определить, как расположена данная прямая относительно данной параболы - пересекается ли, касается или проходит вне еѐ:
а) x y 2 0, y2 8x
б) 8x 3y 15 0, x2 3y ; в) 5x y 15 0, y2 5x .
148
Ответы к задачам для самостоятельного решения
1. |
а) x 1 2 y 2 2 25 , б) x 1 2 y 4 2 8 , |
||
в) x2 y2 16 , |
г) x 1 2 y 4 2 8 ; |
||
2. |
x 4 2 y 1 2 5, |
x 2 2 y 3 2 5 ; |
|
3.а) C(5; 2), R 5,
4.б) C( 2;0), R 8 ,
5.в) уравнение определяет единственную точку ( 5;2) ,
6.г) уравнение не определяет никакого геометрического образа на плоскости;
7.а) k 34 , б) k 43 , в) k 43 ;
8.2;
9. а) |
|
|
x2 |
|
y2 |
|
1, б) |
|
x2 |
|
|
y2 |
|
1, |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
25 |
|
16 |
|
|
100 |
|
64 |
|
|
||||||
10. в) |
|
|
x2 |
|
y2 |
1, |
|
|
г) |
|
x2 |
|
y2 1; |
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
169 |
25 |
|
|
|
|
5 |
|
|
|||||||
11.а) 5 и 3, б) F1( 4;0) , F2 (4;0) , в) 54 , г) x 254 ;
12.3 и 8;
13.4x2 3y2 32x 14y 59 0 ;
14.4x2 5y2 14x 40y 81 0 ;
15.x2 2y2 6x 24y 31 0 ;
|
2 |
|
16. 4; |
|
и (3;2) . |
|
||
|
3 |
|
17. |
|
x2 |
|
y2 |
|
1, б) |
x2 |
|
y2 |
1, в) |
x2 |
|
y2 |
1 , |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
5 |
|
|
|
|
64 |
36 |
|
36 |
64 |
|
|||||
18. |
г) |
|
x2 |
|
y2 |
1 ; |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
144 |
25 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
19. |
|
x 4 |
|
5y 1 0, |
x 10 0 ; |
|
|
|
|
||||||||||
149

20. |
r 2 |
1 |
|
, r |
10 |
1 |
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
1 |
4 |
|
2 |
|
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
21. |
10; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
9 |
|
|
|
|
|
|||||
22. |
10; |
|
|
|
и 10; |
|
; |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||
23. |
а) C(2; 3) , |
a 3,b 4 , |
5 |
, уравнения директрис: |
|||||||||||
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
24. |
5x 19 0 |
и |
|
5x 1 0 , |
уравнения |
асимптот: |
|||||||||
|
4x 3y 17 0 |
|
|
|
|
|
|
||||||||
25. |
4x 3y 0 ; б) C( 5;1) , |
|
a 8 , |
b 6 , |
1.25 , |
||||||||||
уравнения
26.директрис: x 11.4 и x 1.4 , уравнения асимптот:
27.3x 4y 11 0 , 3x 4y 19 0
28.а) y2 6x , б) y2 x , в) x2 12 y , г) x2 6 y ;
29.F(6;0), x 6 0 F (6; 0);
30.(9; 12), (9; - 12);
31.x 14 y2 y 7 ;
32.(- 4; 6) - прямая касается параболы;
33.а) касается параболы, б) пересекает параболу в двух точках, в) проходит вне параболы.
150
