Blatov_lek

Ответы для самостоятельного решения

2.r 2a cos ;

4.а) x a , б) x2 y2 2ay , в) xy a2 ;

171

Лекция 14 Поверхности второго порядка

С теоретико-множественной точки зрения, любая линия или поверхность есть множество точек. Каждое такое множество может обладать некоторыми свойствами.

Математики с древних времен пытались отыскать такие свойства, которые полностью определяли бы такие интуитивно понятные объекты как прямая, кривая, поверхность. Эта задача была окончательно решена лишь в двадцатом веке, когда было введено понятие размерности множества. Мы же ограничимся интуитивным пониманием линии и поверхности.

Поверхности второго порядка находят большое применение в различных областях знания и практики.

Рассмотрим плоскость, на которой геометрическими объектами являются различные линии и требуется изучать их свойства.

Для этого введем на плоскости некоторую декартову систему координат и возьмем на некоторой линии L произвольную точку

M x, y . Если точку M x, y перемещать вдоль L , то ее

координаты будут меняться, но не произвольно. Между ними существует некоторая связь, которая определяется геометрическими свойствами линии L .

y f x или F x, y 0

называется уравнением линии L , если этим соотношениям удовлетворяют координаты любой точки линии L и не удовлетворяют координаты точек, не принадлежащих линии L ..

Таким образом, координаты на плоскости позволяют для каждой линии выписать некоторое уравнение, которое определяется геометрическими свойствами линии, кроме того, оказывается, что каждому уравнению можно поставить в соответствие некоторую линию, и только координаты точек этой линии будут удовлетворять данному уравнению. В связи с этим возникают две задачи.

1.По геометрическим свойствам линии требуется составить

ееуравнение.

172

2. По некоторому уравнению требуется установить геометрические свойства линии, которая этим уравнением определяется.

Эти две задачи и составляют предмет аналитической геометрии на плоскости.

Если взять трехмерное пространство, то к таким геометрическим объектам, как пространственные линии, добавляются новые геометрические объекты - поверхности в трехмерном пространстве.

Поскольку положение точки в пространстве определяется тремя координатами, то и условие, которому удовлетворяют все точки, принадлежащие данной поверхности, аналитически выражается уравнением

F x, y, z 0 .

 Определение Уравнение поверхности - уравнение вида

F x, y, z 0 ,

которому удовлетворяют координаты всех точек данной поверхности, и притом только этих точек.

 Замечание Пространственные линии можно рассматривать как линии пересечения некоторых поверхностей. В дальнейшем, множество всех точек плоскости будем

обозначать как двумерное пространство R2 , а трехмерное пространство - как пространство R3 .

 Замечание Поверхности второго порядка, за исключением случаев сильного вырождения, можно разделить на пять классов:

эллипсоиды,

гиперболоиды,

параболоиды,

конусы

цилиндры.

173

Сфера

Определение Сфера в пространстве R3 - геометрическое место точек, одинаково удаленных от некоторой точки, называемой центром сферы.

Выведем уравнение сферы с центром в точке C(x0 , y0 , z0 ) , точки которой равноудалены от центра C на расстояние r ,

координаты множества точек сферы с центром в точке C и радиусом r и не удовлетворяют координаты никакой точки, не лежащей на сфере. Поэтому уравнение есть искомое уравнение сферы.

 Замечание Заметим, что уравнение сферы радиуса r с центром в начале координат есть уравнение

x2 y2 z2 r2 .

174

Решение

По условию задачи AM BM ,

поэтому

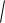x 1 2 y 3 2 z 2 2 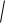x 1 2 y 1 2 z 0 2

После очевидных упрощений, получим x y z 3 0 .

x y z 3 0 .

Пример Какие геометрические образы соответствуют уравнениям:

а) x2 y2 z2 0 , б) x2 y2 z2 4 0 в) x2 y2 0

Решение

а) это уравнение определяет точку O 0,0,0 , так как координаты лишь этой точки удовлетворяют уравнению.

175

б) это уравнение определяет пустое множество точек, так как в множестве действительных чисел нет таких, которые

Очевидно, что результат пересечения есть окружность в плоскости Oxy с центром в начале координат и радиуса r , а ее уравнение, как следует из заданной системы, будет x2 y2 z2 r2 .

Из приведенных частных примеров видно, что уравнениям, в

которые входят три, две, одна неизвестная, в пространстве R3 соответствует некоторая поверхность, а пересечение поверхностей определяет линию.

Исключением являются случаи, когда поверхность (можно привести примеры и с линией) "вырождается" в отдельные точки, в линии или представляет пустое множество точек.

Заметим, что поверхности принято классифицировать на

алгебраические и трансцендентные.

 Определение Поверхность называется алгебраической,

если в некоторой прямоугольной декартовой системе координат

первого порядка,

176

поверхность второго порядка.

 Определение Всякая неалгебраическая поверхность

называется трансцендентной.

 Определение Поверхность второго порядка -

геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению

ax2 by2 cz2 dxy fxz gyz hx ky lz m 0

Эллипсоид: Однополостной гиперболоид:

Гиперболический параболоид

177

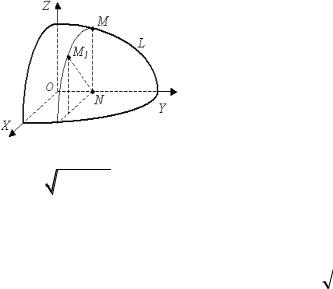
Поверхности вращения

Поверхность вращения — поверхность, созданная при вращении образующей вокруг оси. Например, если прямая пересекает ось вращения, то при еѐ вращении получится

коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения. Одна и та же поверхность может быть получена вращением самых разнообразных кривых.

Поверхность вращения является объектом изучения в математическом анализе, аналитической геометрии

 Определение Поверхность вращения - поверхность,

образованная вращением какой-либо плоской линии вокруг прямой, лежащей в плоскости этой линии.

Для вывода уравнения поверхности вращения необходимо выбрать систему координат. Чтобы уравнение поверхности вращения выглядело проще, ось вращения принимают за одну из координатных осей.

координаты точки M x, y, z удовлетворяют уравнению

178

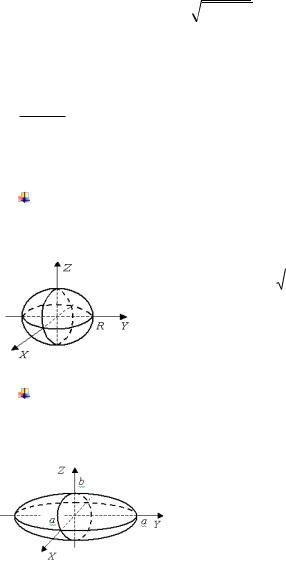
F y, 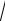x2 z2 0

Уравнение и есть искомое уравнение поверхности вращения. Таким образом, чтобы получить уравнение поверхности, образованной вращением линии L , лежащей в плоскости Oyz ,

вокруг оси Oy , нужно в уравнении этой линии заменить z на

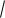x2 z2 .Аналогичные правила будут иметь место и по отношению к уравнениям поверхностей, полученных вращением плоских линий вокруг других координатных осей.

Пример Найти уравнение поверхности вращения

179

Эллипсоиды

 Определение Эллипсоид – поверхность, которая в некоторой системе декартовых прямоугольных координат, определяемая уравнением

эллипсоид трехосный, a b c - эллипсоид есть сфера.

Если две из величин одинаковы, то эллипсоид является поверхностью вращения, a b , - то ось вращения OZ .

В случае, когда пара полуосей имеет одинаковую длину, эллипсоид может быть получен вращением эллипса вокруг одной из его осей. Такой эллипсоид называют эллипсоидом вращения или сфероидом.

С помощью метода параллельных сечений исследуем форму эллипсоида.

Рассмотрим сечение плоскостями, параллельными плоскости

OXY .

эллипсу с полуосями

Аналогично при рассмотрении сечений эллипсоида с плоскостями OXZ и OYZ. Сечением эллипсоида любой плоскостью является эллипс (в частном случае круг).

 Определение Мнимый эллипсоид – поверхность определяемая уравнением

180