Blatov_lek

A(x x0 ) B( y y0 ) C(z z0 ) 0

- уравнение называют - уравнением плоскости, проходящей

через заданную точку M0 (x0 , y0 , z0 ) .

Отметим, что вектор n A, B,C называют нормальным

получаем: Ax By Cz Ax0 By0 Cz0 0 ,

Или A(x x0 ) B( y y0 ) C(z z0 ) 0 .

а это есть уравнение плоскости, проходящей через точку

(x0 , y0 , z0 ) и имеющую нормальный вектор n A, B,C . Следовательно, и равносильное ему уравнение

Ax By Cz D 0 определяет плоскость.

Теорема доказана.

Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M1(x1 , y1, z1) ,

M2 (x2 , y2 , z2 ) , M3 (x3 , y3, z3 ) принадлежащие плоскости и не лежащие на одной прямой.

Возьмем текущую точку M (x, y, z) плоскости и организуем три вектора

M1M2 x2 x1, y2 y1, z2 z1

M1M3 x3 x1, y3 y1, z3 z1

91

M1M x1 x, y1 y, z1 z

Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть

есть уравнение плоскости, проходящей через три заданные точки M1 , M 2 , M3 .

При решении задач часто используется так называемое

Уравнение называют уравнением плоскости в отрезках на осях, т.к. числа a,b,c имеют простой геометрический смысл:

a - абсцисса точки пересечения плоскости с осью Ox , b - ордината точки пересечения плоскости с осью Oy , с -

аппликата точки пересечения плоскости с осью Oz . Действительно, точка пересечения плоскости с осью,

92

Отсюда получаем x D .

A

Рассмотрим особенность расположения плоскости, заданной общим уравнением, если некоторые коэффициенты этого уравнения обращаются в нуль.

A 0 , By Cz D 0 - плоскость параллельна оси Ox

 Замечание Если плоскость параллельна какой-нибудь координатной оси, то в ее уравнении отсутствует член, содержащий координату, одноименную с этой осью.

Пример Найти уравнение плоскости, параллельной оси Oz и проходящей через точки A 2,3,1 , B 1,2,4

93

системы двух уравнений с тремя неизвестными, подставляя в (*), получаем x 3y 7 0

Нормальное уравнение плоскости

Пусть дана плоскость, проведем через начало координат прямую, перпендикулярно к плоскости – эта прямая нормаль, точка P – точка в которой прямая пересекает плоскость.

На нормали введем положительное направление от точки О к

квадратов коэффициентов при текущих координатах должна быть равна 1, а свободный член должен быть отрицателен.

Умножим общее уравнение на множитель

Ax By Cz D 0

94

A cos , B cos , C cos D p ,

A2 B2 C2

Из уравнения D p , следует, что знак нормирующего

множителя противоположен знаку свободного члена нормируемого уравнения.

Для приведения общего уравнения плоскости к нормальному виду обе части его умножают на нормирующий множитель, знак выбирают противоположный знаку свободного члена в общем уравнении плоскости.

Если D 0 знак выбирается произвольно.

Расстояние от точки до плоскости

 Определение Отклонением точки M * от данной

плоскости называется число d , если M * лежит по ту сторону от плоскости, куда идет положительное направление нормали, и

Чтобы найти отклонение какой-либо точки M * от некоторой прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки M* .

x* cos x* cos x* cos

x* cos y* cos z* cos p

95

M 4,3,1 . Найти отклонение точки от плоскости.

удалена от плоскости на расстояние 2.

Взаимное расположение двух плоскостей Угол между двумя плоскостями

Линейный угол, являющейся мерой двугранного угла между плоскостями, равен углу между перпендикулярами к этим плоскостям.

Для двух плоскостей, заданных уравнениями

A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0

96

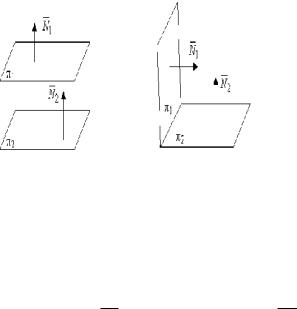
Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей.

Условие параллельности двух плоскостей

Пусть даны две плоскости

A1 x B1 y C1 z D1 0A1 x B1 y C1 z D2 0

Данные плоскости параллельны, когда их нормальные векторы

N1 A1 , B1 , C1 , N2 A2, B2,C2 коллинеарны.

Условие перпендикулярности двух плоскостей

Данные плоскости перпендикулярны, когда их нормальные

векторы N1 A1 , B1 , C1 , N2 A2 , B2 , C2 ,

перпендикулярны.

Условие перпендикулярности двух плоскостей

97

Контрольные вопросы по теме «Плоскость»

1.Написать векторное уравнение плоскости и объяснить смысл величин, входящих в это уравнение.

2.Написать общее уравнение плоскости

3.Написать уравнение плоскости, проходящей через заданную точку. Объяснить смысл величин, входящих в это уравнение.

4.Как вычислить угол между плоскостями?

5.Условия параллельности и перпендикулярности двух плоскостей.

5.Написать уравнение плоскости, проходящей через ось Ох и точку М1 (0;- 2;3).

6.Найти угол между плоскостями:

а) x 2y 2z 8 0 и x z 6 0 , б) x 2z 6 0 и x 2y 4 0 ,

в) x 3z 8 0 и 2x 6z 7 0,

г) 2x 3y z 3 0 и x y z 5 0 .

7. Написать уравнение плоскости, проходящей через точку M1 1, 1,2 и перпендикулярной к плоскостям x 2y x 4 0 и x 2y 2z 4 0 .

98

8.Написать уравнение плоскости, проходящей через точки M1 1, 2,0 и M 2 1,1,2 и перпендикулярной к

11.Найти расстояние между параллельными плоскостями

4x 3y 5z 12 0 и 4x 3y 5z 8 0 .

12.Написать уравнение плоскости, проходящей через

13.Найти точку пересечения плоскостей 2x y 3z 9 0 ,

x2y 2z 3 0 , 3x y 4z 6 0 .

14.Написать уравнение плоскости, проходящей через точки0, 5,0 , M 2 0,0,2 и перпендикулярной к

плоскости x 5y 2z 10 0 . Построить ее.

Ответы к задачам для самостоятельного изучения

1.cos 72 , cos 34 , cos 76 ;

2.x 4y 2z 2 0 ;

3.x y z 3 0 ;

4.3y 2z 0 ;

5.а) 450 , б) 78030 , в) 00 , г) 900 ;

6.2x 3y 4z 3 0 ;

7.2x 2y z 2 0 ;

8.3;

9.6 ;

10.22;

99

11.x 8y 9z 21 0 ;

12.1, 1,2 ;

13.2y 5z 10 0 .

100