
- •Содержание
- •1 Формальные языки и грамматики
- •1.1 Основные понятия теории формальных языков
- •Определение Цепочка, которая не содержит ни одного символа, называется пустой цепочкой и обозначается .
- •1.2 Способы задания языков
- •1.2.1 Формальные грамматики
- •1.2.1.1 Определение формальной грамматики
- •Определение Цепочка (vtvn)* выводима из цепочки в грамматике(обозначается*), если существует последовательность цепочек (n0) такая, что .
- •1.2.1.3 Эквивалентность грамматик
- •1.2.2 Формы Бэкуса - Наура
- •1.2.3 Диаграммы Вирта
- •1.2.5 Механизмы распознавания языков
- •1.2.5.1 Определение распознавателя
- •1.2.5.2 Схема работы распознавателя
- •1.2.5.3 Классификация распознавателей
- •2 Регулярные грамматики и языки
- •2.1 Регулярные выражения
- •2.2 Лемма о разрастании языка
- •2.3 Конечные автоматы
- •2.3.1 Определение конечного автомата
- •2.3.2 Распознавание строк конечным автоматом
- •Существуют следующие способы представления функции переходов: - командный способ.Каждую команду ка записывают в форме , где.
- •2.3.3 Преобразование конечных автоматов
- •2.3.3.1 Преобразование конечного автомата к детерминированному виду
- •Алгоритм Преобразование нка в дка
- •2.3.3.2 Минимизация конечного автомата
- •2.3.3.2.1 Устранение недостижимых состояний ка
- •2.3.3.2.2 Объединение эквивалентных состояний ка Алгоритм Объединение эквивалентных состояний ка
- •2.4 Взаимосвязь способов определения грамматик
- •2.4.1 Построение ка по регулярной грамматике
- •Выход:ка.
- •3 Контекстно-свободные языки и грамматики
- •3.1 Задача разбора
- •3.1.1 Вывод цепочек
- •Определение Цепочка (vtvn)* выводима из цепочки в грамматике(обозначается*), если существует последовательность цепочек (n0) такая, что .
- •3.1.2 Дерево разбора
- •3.1.2.1 Нисходящее дерево разбора
- •3.1.2.2 Восходящее дерево разбора
- •3.1.3 Однозначность грамматик
- •3.2 Преобразование кс-грамматик
- •3.2.1 Проверка существования языка грамматики
- •3.2.2 Устранение недостижимых символов
- •Алгоритм Устранение нетерминалов, не порождающих терминальных строк Вход: кс-грамматика.
- •Алгоритм Устранение недостижимых символов Вход: кс-грамматика.
- •Определим множество достижимых символов z грамматики g, т.Е. Множество
- •3.2.3 Устранение -правил Алгоритм Устранение -правил Вход: кс-грамматика.
- •3.2.4 Устранение цепных правил Алгоритм Устранение цепных правил Вход: кс-грамматика.
- •3.2.5 Левая факторизация правил Алгоритм Устранение левой факторизации правил Вход: кс-грамматика.
- •3.2.6 Устранение прямой левой рекурсии Алгоритм Устранение прямой левой рекурсии Вход: кс-грамматика.
- •3.3 Автомат с магазинной памятью
- •3.3.1 Определение мп-автомата
- •3.3.2 Разновидности мп-автоматов
- •3.3.3 Взаимосвязь мп-автоматов и кс-грамматик
- •3.3.3.1 Построение мп-автомата по кс-грамматике
- •3.3.3.2 Построение расширенного мп-автомата по кс-грамматике
- •3.4 Нисходящие распознаватели языков
- •3.4.1 Рекурсивный спуск
- •3.4.1.1 Сущность метода
- •3.4.1.2 Достаточные условия применимости метода рекурсивного спуска
- •3.4.2 Распознаватели ll(k)-грамматик
- •3.4.2.1 Определение ll(k)-грамматики
- •3.4.2.2 Необходимое и достаточное условие ll(1)-грамматики
- •3.4.2.3 Построение множества first(1, a)
- •3.4.2.4 Построение множества follow(1, a)
- •3.4.2.5 Алгоритм «сдвиг-свертка» для ll(1)-грамматик
- •Шаг 6. Получили следующую цепочку вывода:
- •3.5.1.1.2 Поиск основы сентенции грамматики
- •3.5.1.1.3 Построение множеств l(a) и r(a)
- •3.5.1.1.5 Алгоритм «сдвиг - свертка» для грамматик простого предшествования
- •Шаг 3. Функционирование распознавателя для цепочки (((aa)a)a) показано в таблице 3.9.
- •3.5.1.2 Грамматика операторного предшествования
- •3.5.1.2.1 Определение грамматики операторного предшествования
- •3.5.1.2.2 Построение множеств Lt(a) и Rt(a)
- •3.5.1.2.4 Алгоритм «сдвиг-свертка» для грамматики операторного предшествования
- •3.5.2 Распознаватели lr(k)-грамматик
- •3.6 Соотношение классов кс-грамматик и кс-языков
- •3.6.1 Соотношение классов кс-грамматик
- •3.6.2 Соотношение классов кс-языков
- •4 Принципы построения языка
- •4.1 Лексика, синтаксис и семантика языка
- •4.2 Определение транслятора, компилятора, интерпретатора и ассемблера.
- •4.3 Общая схема работы компилятора
- •4.4 Лексический анализ
- •4.4.1 Задачи лексического анализа
- •4.4.2 Диаграмма состояний с действиями
- •4.4.3 Функция scanner
- •4.5 Синтаксический анализатор программы
- •4.5.1 Задача синтаксического анализатора
- •4.5.2 Нисходящий синтаксический анализ
- •Теорема Достаточные условия применимости метода рекурсивного спуска
- •4.6 Семантический анализ программы
- •4.6.1 Обработка описаний
- •4.6.2 Анализ выражений
- •4.6.3 Проверка правильности операторов
- •4.7 Генерация кода
- •4.7.1 Формы внутреннего представления программы
- •4.7.1.1 Тетрады
- •4.7.1.2 Триады
- •4.7.1.3 Синтаксические деревья
- •4.7.1.4 Польская инверсная запись
- •Составной оператор begin s1; s2;...; Sn end в полиЗе записывается как s1 s2... Sn.
- •4.7.1.5 Ассемблерный код и машинные команды
- •4.7.2 Преобразование дерева операций в код на языке ассемблера
- •4.8 Оптимизация кода
- •4.8.1 Сущность оптимизации кода
- •4.8.2 Критерии эффективности результирующей программы
- •4.8.3 Методы оптимизации кода
- •4.8.4 Оптимизация линейных участков программ
- •4.8.4.1 Свертка объектного кода
- •4.8.4.2 Исключение лишних операций
- •4.8.5 Оптимизация логических выражений
- •4.8.6 Оптимизация циклов
- •4.8.7 Оптимизация вызовов процедур и функций
- •4.8.9 Машинно-зависимые методы оптимизации
- •4.8.9.1 Распределение регистров процессора
- •4.8.9.2 Оптимизация кода для процессоров, допускающих распараллеливание вычислений
- •5 Формальные методы описания перевода
- •5.1 Синтаксически управляемый перевод
- •5.1.1 Схемы компиляции
- •5.1.4 Практическое применение су-схем
- •5.2 Транслирующие грамматики
- •5.2.1 Понятие т-грамматики
- •5.3 Атрибутные транслирующие грамматики
- •5.3.1 Синтезируемые и наследуемые атрибуты
- •5.3.2 Определение и свойства ат-грамматики
- •5.3.3 Формирование ат-грамматики
- •Решение
2.3.3.2.1 Устранение недостижимых состояний ка
Алгоритм Устранение недостижимых состояний КА
Вход: КА
![]() .
.
Выход: КА
![]() .
.
Шаг 1. Поместить
начальное состояние КА в список достижимых
состояний
![]() ,
т.е.
,
т.е.![]() .
.
Шаг 2. Для новых
элементов списка достижимых состояний
пополнить список группой их
состояний-приемников, отсутствующих в
списке, т.е.
![]() .
.
Шаг 3. Повторить
шаг 2, пока список достижимых состояний
не перестанет меняться. То есть, если
![]() ,то i=i+1,
иначе
,то i=i+1,
иначе ![]() .
.
Шаг 4. Исключить
из множества Q
состояний КА все состояния, отсутствующие
в списке Qд
достижимых
состояний, т.е.
![]() .
.
Шаг 5. Исключить
недостижимые заключительные состояния
и функции переходов, содержащие
недостижимые состояния, т.е.
![]() ,
,
![]() .
.
Пример Устранить
недостижимые состояния КА![]() ,
гдеQ = {A,
B, C,
D, E,
F, G},T= {a,
b},H
= {A}, Z= {D, E}
и функция переходов задана таблицей
2.4. Граф исходного КАМпредставлен
на рисунке 2.3.
,
гдеQ = {A,
B, C,
D, E,
F, G},T= {a,
b},H
= {A}, Z= {D, E}
и функция переходов задана таблицей
2.4. Граф исходного КАМпредставлен
на рисунке 2.3.
Таблица 2.4 – Функция переходов конечного автомата M
|
F |
A |
B |
C |
D |
E |
F |
G |
|
a |
B |
|
|
C |
B |
D |
F |
|
b |
C |
D |
E |
E |
D |
G |
E |
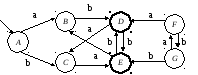
Рисунок 2.2 – Граф исходного конечного автомата М
Последовательность устранения недостижимых состояний КА имеет вид:
Q0 = {A};
Q1 = {A, B, C};
Q2 = {A, B, C, D, E};
Q3 = {A, B, C, D, E}; т.к. Q2 = Q3, то Qд = {A, B, C, D, E}.
Qн
= {F,
G
};
![]() =
{A,
B,
C,
D,
E};
=
{A,
B,
C,
D,
E};
![]() =
{D,
E}.
=
{D,
E}.
Функция переходов
автомата
![]() представлена в таблице 2.6.
представлена в таблице 2.6.
Таблица 2.5 - Функция
переходов автомата
![]()
-
F
A
B
C
D
E
a
B
C
B
b
C
D
E
E
D
Г
b![]() после устранения недостижимых состояний
представлен на рисунке 2.5.
после устранения недостижимых состояний
представлен на рисунке 2.5.
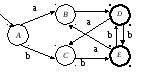
Рисунок 2.3 - Граф
КА
![]() после устранения недостижимых состояний
после устранения недостижимых состояний
2.3.3.2.2 Объединение эквивалентных состояний ка Алгоритм Объединение эквивалентных состояний ка
Вход: КА
![]() без недостижимых состояний.
без недостижимых состояний.
Выход: минимальный
КА
![]() .
.
Шаг 1. На первом шаге строим нулевое разбиение R(0), состоящее из двух классов эквивалентности: заключительные состояния КА -Zи не заключительные -Q-Z.
Шаг 2. На очередном шаге построения разбиения R(n) в классы эквивалентности включить те состояния, которые по одинаковым входным символам переходят вn-1 эквивалентные состояния, т.е.
![]() .
.
Шаг 3. До тех пор, пока R(n) R(n-1) полагаемn=n+1 и идем к шагу 2.
Шаг 4. Переобозначить оставшиеся неразбитые группы состояний и включить их в таблицу новых обозначений состояний автомата.
Шаг 5. Определить
эквивалентный КА
![]() в новых обозначениях.
в новых обозначениях.
Пример Минимизировать конечный автомат из предыдущего примера.
Последовательность построения разбиений будет иметь вид:
R(0) = {{A, B, C}, {D, E}}, n= 0;
R(1) = {{A}, {B, C}, {D, E}}, n= 1;
R(2) = {{A}, {B, C}, {D, E}}, n=2.
Т.к. R(1) = R(2), то искомое разбиение построено.
Переобозначим оставшиеся неразбитые группы состояний:
X={B, C}, Y={D, E}.
Получим минимальный
автомат
![]() ,
где
,
где
![]() ={A,
X, Y},
={A,
X, Y},
![]() ={Y}.
={Y}.
Функция переходов
автомата
![]() представлена
в таблице 2.7.
представлена
в таблице 2.7.
Таблица 2.6 - Функция
переходов автомата
![]()
-
A
X
Y
a
X
X
b
X
Y
Y
Граф переходов конечного автомата после его минимизации показан на рисунке 2.4.
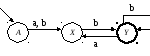
Рисунок 2.4 – Граф
минимального ДКА
![]()
