Правило вычисления векторного произведения
Для заданных в декартовом базисе {i¸j¸k} векторов
и
их векторное произведение может быть найдено по формуле
Из определения и свойств следует и
Основные приложения векторного произведения
Если
S∆
- площадь треугольника построенного
на векторах
и
,
а φ
- угол между ними то
,
,
.
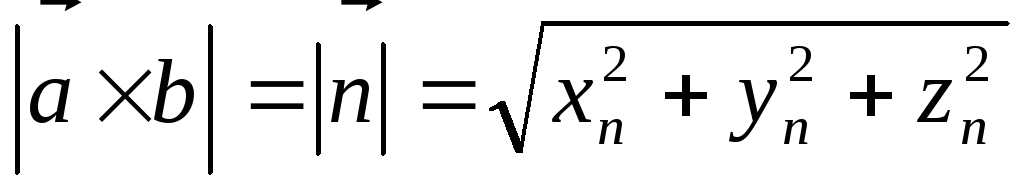Если
h - высота пирамиды (параллелепипеда
(призмы)), построенного (смотри следующий
ниже рисунок) на векторах
как на ребрах, то она может быть
найдена по формуле
Смешанное произведение векторов.
Смешанным
произведением
трех векторов
называется число, равноескалярному
произведению векторного произведения
первых двух векторов на третий.
Обозначив
смешанное произведение символом (
),
по определению, имеем
(
)
=
·
В декартовом базисе смешанное произведение векторов
,
,
вычисляется по формуле
(
)
=
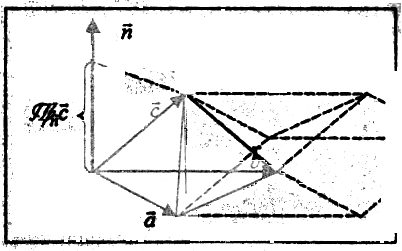
Геометрически
модуль смешанного произведения (
)
равен объему параллелепипеда,
построенного на векторах
как на ребрах. Из этого, в частности,
вытекает, что он же равен удвоенному
объему соответствующе призмы и
«ушестеренному» объему пирамиды с
теми же ребрами.
Пример.
В пирамиде (рис. 9), построенной на
векторах
,
,
Найти
площадь основания, построенного на
и
;
высоту, опущенную из «конца»
и проверить «школьную» формулу объема
с помощью смешанного произведения.
Решение:
С другой стороны
.
Азы аналитической геометрии. Уравнения прямой на плоскости.
П
рямую
(l), «вложенную
в декартову систему координат (д.с.к)
на плоскости (рис. 10), вполне определяют
лежащая на ней фиксированная точка
М0
(х0,у0,z0)
и так называемый направляющий вектор
коллинеарный этой прямой. Условием
принадлежности «текущей» (произвольной)
точки М (х,у,z) к этой прямой является
равенство
(t - «коэффициент коллинеарности»). Переписанное в виде
(1)
оно именуется как векторно – параметрическое уравнение прямой. Из него вырастает целый букет» уравнений все той же прямой. Это:
параметрические уравнения прямой -
; (2)
каноническое уравнение прямой -
; (3)
уравнение
прямой с нормальным вектором
,
содержащей точку М0
(х0,у0,z0)
-
А·(x-x0)+B·(y-y0)=0
(4)
уравнение прямой, проходящей через две точки М0 (х0,у0,z0) и М1 (х1,у1,z1) -
;
(5)
уравнение прямой с угловым коэффициентом k, содержащей точку М0 (х0,у0,z0) -
;
(6)
«школьное» уравнение прямой -
;
(7)
общее уравнение прямой
.
(8)
Угол между прямыми.
У
гол
θ между прямыми (1) и (2) (рис. 11) с
известными угловыми k1
и k2
может быть найден по формуле
Отсюда, если прямые перпендикулярны, то
k1·k2
= -1
