
- •Волжская государственная академия водного транспорта
- •Основные понятия из линейной алгебры и дифференциального исчисления.
- •В. Даль «Толковый словарь…» матричная азбука Основные определения и обозначения
- •Действия с матрицами
- •Определители матриц.
- •Таким образом, по определению для любого натурального n имеем
- •Свойства определителей
- •Обратная матрица
- •Ранг матрицы.
- •Решение систем
- •I. Метод обратной матрицы.
- •II. Правило Крамера.
- •III. Метод Гаусса
- •Векторная азбука Основные определение и обозначения
- •Линейные действия с векторами.
- •Базис и координаты.
- •Система координат «точечного» пространства.
- •Задача о делении отрезка в данном отношении.
- •Правило вычисления векторного произведения
- •Основные приложения векторного произведения
- •Смешанное произведение векторов.
- •Азы аналитической геометрии. Уравнения прямой на плоскости.
- •Угол между прямыми.
- •Расстояние от точки до прямой.
- •Уравнения плоскости в пространстве.
- •Расстояние от точки до плоскости.
- •Уравнение прямой в пространстве.
- •Параметрические уравнения прямой –
- •Канонические уравнения прямой
- •Расстояние от точки до прямой
- •Замечания о взаимном расположении.
- •Кривые второго порядка.
- •Азбука дифференциального исчисления. Переменные величины.
- •Предел переменной
- •«Монотонная и ограниченная последовательность имеет предел»
- •Характеристический признак существования предела.
- •Сравнение бесконечно малых переменных величин.
- •Характеристическое свойство бесконечно малых
- •Непрерывность.
- •Асимптоты функции
- •Свойства непрерывных функций
- •Производные фоункции
- •Правило дифференцирования сложной функции
- •Дифференциал функции.
- •Арифметические свойства дифференциала
- •Производные и дифференциалы высших порядков.
- •Приложения производных к исследованию функций.
- •Азы дифференциального исчисления функции нескольких переменных. Основные определения
- •Производные функции многих переменных.
- •Дифференцирование неявных функций
- •Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности.
- •Старшие производные
- •Экстремумы функций двух переменных.
- •Векторная функция скалярного аргумента
- •Задания к контрольной работе № 1
- •Задания на контрольную работу № 2
- •Литература
Дифференцирование неявных функций
С помощью частных производных вычисляются производные так называемых неявных функций.
Говорят,
что переменная у является неявной
(неявно заданной) функция от переменной
х, если эта зависимость определяется
уравнение вида
![]() ,
то есть уравнением не разрешенным
относительно у. Точно также можно
говорить, что уравнение вида
,
то есть уравнением не разрешенным
относительно у. Точно также можно
говорить, что уравнение вида![]() определяет неявно заданную функцию
«z от х и у», то есть неявную функцию
двух переменных. Можно показать, что
в первом случае - для неявной функции
«у от х» - производная «от у по х»
находится по формуле.
определяет неявно заданную функцию
«z от х и у», то есть неявную функцию
двух переменных. Можно показать, что
в первом случае - для неявной функции
«у от х» - производная «от у по х»
находится по формуле.
![]()
Частные
производные от неявной функций двух
переменных -
![]() - могут быть найдены по формулам
- могут быть найдены по формулам
![]()
![]()
,
,
Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности.
Полный дифференциал функции z=f(x¸y) двух переменных мы определим как выражение вида:
![]()
Пример: z=x·y3;dz=y3·∆x+3xy2·∆y.
Его
компоненты - слагаемые обзываются
соответствующими частными дифференциалами
(«по х» и «по у»). Как и дифференциал
функции одной переменно величина dz
является главной линейной частью
так называемого полного приращения
![]() и связан с ним соотношением
и связан с ним соотношением
![]()
где
![]() ,
а γ - некая бесконечно малая. Используя
геометрический смысл частных
производных, показывается, что для
поверхности - графика функцииz=f(x¸y)
уравнение касательной плоскости в
произвольной ее точке М0(х0,
у0,
f(x0¸y0))
можно записать в виде
,
а γ - некая бесконечно малая. Используя
геометрический смысл частных
производных, показывается, что для
поверхности - графика функцииz=f(x¸y)
уравнение касательной плоскости в
произвольной ее точке М0(х0,
у0,
f(x0¸y0))
можно записать в виде
![]()
Уравнение соответствующей нормали - прямой, перпендикулярной к касательной плоскости в точке касания можно записать так:
![]() .
.
 На
рисунке условно изображены касательная
плоскость и нормаль к графику некоторой
функции в т. М0.
Сравнивая уравнение касательной
плоскости и соответствующий дифференциал
функции, замечаем, что дифференциал
(являясь главной частью полного
приращения) выражает полное приращение
аппликаты касательной плоскости к
графику этой функции в данной точке.
На
рисунке условно изображены касательная
плоскость и нормаль к графику некоторой
функции в т. М0.
Сравнивая уравнение касательной
плоскости и соответствующий дифференциал
функции, замечаем, что дифференциал
(являясь главной частью полного
приращения) выражает полное приращение
аппликаты касательной плоскости к
графику этой функции в данной точке.
Старшие производные
Так же как и для функции одной переменной, определяются вторые, третьи, ... .. «энные» частные производные. Правда, наличие двух и более переменных делает «букет» из них более богатым. Так, в частности, по определению и обозначению
 -
вторые «смешанные» производные.
-
вторые «смешанные» производные.
 -
вторые «чистые» производные.
-
вторые «чистые» производные.
![]() -
третья смешанная производная.
-
третья смешанная производная.
Аналогичным образом определяется и производные более высокого порядка.
Пример:
![]()
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
...
,
...
Экстремумы функций двух переменных.
С
помощью частных производных можно
отыскать точки экстремумов функции
и определить их характер. Так необходимым
признаком
того, что точка
![]() является точкой минимума (максимума)
то есть точкой экстремума дифференцируемой
функции,является
выполнение
в этой точке условий:
является точкой минимума (максимума)
то есть точкой экстремума дифференцируемой
функции,является
выполнение
в этой точке условий:
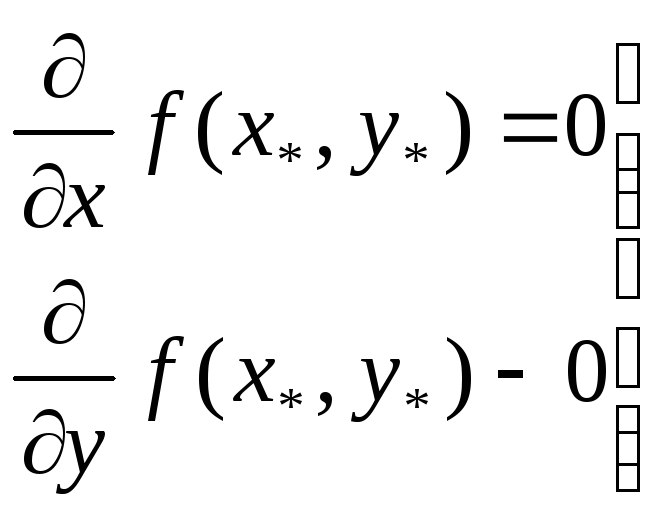 .
.

Точки, в которых эти условия выполняются, по – прежнему будем называть критическими.
Достаточным признаком того, что критическая точка действительно экстремальна, является выполнение в этой точке неравенства

При этом, если
![]() ,
то
,
то
![]() - точка максимума, а если
- точка максимума, а если![]() ,
то
,
то![]() - точка минимума.
- точка минимума.
Если
![]() ,
то критическая точка не экстремальна
(она называется в этом случае седловой
точкой). Если же
,
то критическая точка не экстремальна
(она называется в этом случае седловой
точкой). Если же![]() ,
то вопрос о характера критической
точки открыт (требуются дополнительные
исследования).
,
то вопрос о характера критической
точки открыт (требуются дополнительные
исследования).
Пример: Найти экстремуму функции
![]() .
.
Решение
 ,
отсюда М0
(-2,3) - критическая точка
,
отсюда М0
(-2,3) - критическая точка
![]() ;
;
![]() ;
;![]() М0
(-2,3) - точка минимума.
М0
(-2,3) - точка минимума.
