
terver
.docx22.Понятие случайного процесса и его основные характеристики. Случайным процессом X(f) называется процесс, значение которого при любом значении аргумента t является случайной величиной. Другими словами, случайный процесс представляет собой функцию, которая в результате испытания может принять тот или иной конкретный вид, неизвестный заранее. При фиксированном t = to X(to) представляет собой обычную случайную величину, т.е. сечение случайного процесса в момент /Ь. Аналогично тому, как в гл. 3 записана случайная величина в виде функции элементарного события со, появляющегося в результате испытания, случайный процесс можно записать в виде функции двух переменных X(t, со), где go G Q, t E T9 X(t, со) G S и ю — элементарное событие, Я — пространство элементарных событий, Т — множество значений аргумента /, s — множество возможных значений случайного процесса X(t, со). Реализацией случайного процесса X(t, со) называется неслучайная функция x(t), в которую превращается случайный процесс X(t) в результате испытания (при фиксированном ю), т.е. конкретный вид, принимаемый случайным процессом X(t), его траектория. Таким образом, случайный процесс X(t, со) совмещает в себе черты случайной величины и функции. Если зафиксировать значение аргумента /, случайный процесс превращается в обычную случайную величину, если зафиксировать ю, то в результате каждого испытания он превращается в обычную неслучайную функцию. В дальнейшем изложении опустим аргумент со, но он будет подразумеваться по умолчанию.
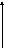




На
рис. изображено (сверху Х слева t
по середине тоже t)
( и таких линий много идут и вниз и верх)
несколько реализаций некоторого
случайного процесса. Пусть сечение
этого процесса при данном t является
непрерывной случайной величиной. Тогда
случайный процесс X(t) при данном t
определяется плотностью вероятности
f(х,
t). Очевидно, что плотность f(х,
t) не является исчерпывающим описанием
случайного процесса X(t), ибо она не
выражает зависимости между его сечениями
в разные моменты времени. Случайный
процесс X(t) представляет собой совокупность
всех сечений при всевозможных значениях
t, поэтому для его описания необходимо
рассматривать многомерную случайную
величину (X(t\)( X(t2),..., X(tn)), состоящую из
всех сечений этого процесса. В принципе
таких сечений бесконечно много, но для
описания случайного процесса удается
часто обойтись относительно небольшим
количеством сечений. Говорят, что
случайный процесс имеет порядок п, если
он полностью определяется плотностью
совместного распределения f(*b
*2v-5 Xn> h> *2v5 *l)
l
произвольных сечений процесса, т.е.
плотностью я-мерной случайной величины
(X(t\), Д^),.--? ДО)? где X(tj) — сечение случайного
процесса ДО в момент времени ti9 /=
1,2,...,я. Как и случайная величина, случайный
процесс может быть описан числовыми
характеристиками.

31.Цепи Маркова представляют один из видов Марковского случайного процесса, рассматриваемого (в иной терминологии). Процесс работы СМО представляет собой случайный процесс. Процесс называется процессом с дискретными состояниями, если его возможные состояния S\, /S2, »%••• можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны. Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Это означает, что состояние СМО меняется скачком в случайные моменты появления каких-то событий (например, прихода новой заявки, окончания обслуживания и т.п.). Математический анализ работы СМО существенно упрощается, если процесс этой работы — марковский. Случайный процесс называется марковским или случайным процессом без последействия, если для любого момента времени *b вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент /Ь и не зависят от того, когда и как система пришла в это состояние. Например, процесс игры в шахматы; система S — группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившихся на доске в момент /q. Вероятность того, что в момент t> t0 материальный перевес будет на стороне одного из противников, зависит в первую очередь от того, в каком состоянии находится система в данный момент /q, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента to. В ряде случаев предысторией рассматриваемых процессов можно просто пренебречь и применять для их изучения марковские модели. При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой— так называемым графом состояний.Обычно состояния системы изображаются прямоугольниками (кружками), а возможные переходы из состояния в состояние — стрелками (ориентированными дугами), соединяющими состояния.
32.Условия
стационарного режима для цепи Маркова
и определения финальных вероятностей.
Опред1.Цепью
Маркова называют последовательность
испытаний, в каждом из которых появляется
одно и только одно из ![]() несовместных
событий
несовместных
событий ![]() полной
группы, причем условная вероятность
полной
группы, причем условная вероятность ![]() того,
что в
того,
что в ![]() -м
испытании наступит событие
-м
испытании наступит событие ![]() ,
при условии, что в
,
при условии, что в ![]() -м
испытании наступило событие
-м
испытании наступило событие ![]() ,
не зависит от результатов предшествующих
испытаний.
Ясно,
что ЦМ – это марковский процесс, множество
состояний которого конечно или счетно.
Понятно также, что можно анализировать
многомерные ЦМ. Опред2.
Вероятностное
распределение
,
не зависит от результатов предшествующих
испытаний.
Ясно,
что ЦМ – это марковский процесс, множество
состояний которого конечно или счетно.
Понятно также, что можно анализировать
многомерные ЦМ. Опред2.
Вероятностное
распределение ![]() ,
где
,
где 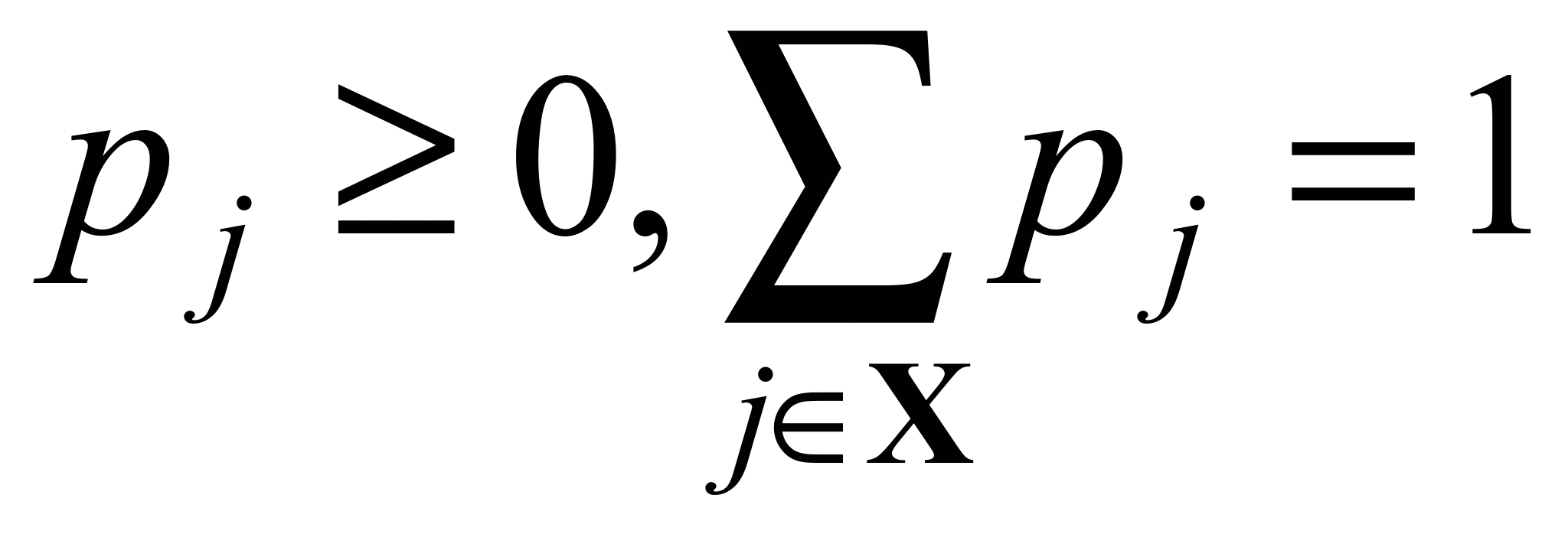 называется
стационарным распределением цепи
Маркова, если для любого состояния
называется
стационарным распределением цепи
Маркова, если для любого состояния![]() и
любого
и
любого![]() выполняется
равенство
выполняется
равенство
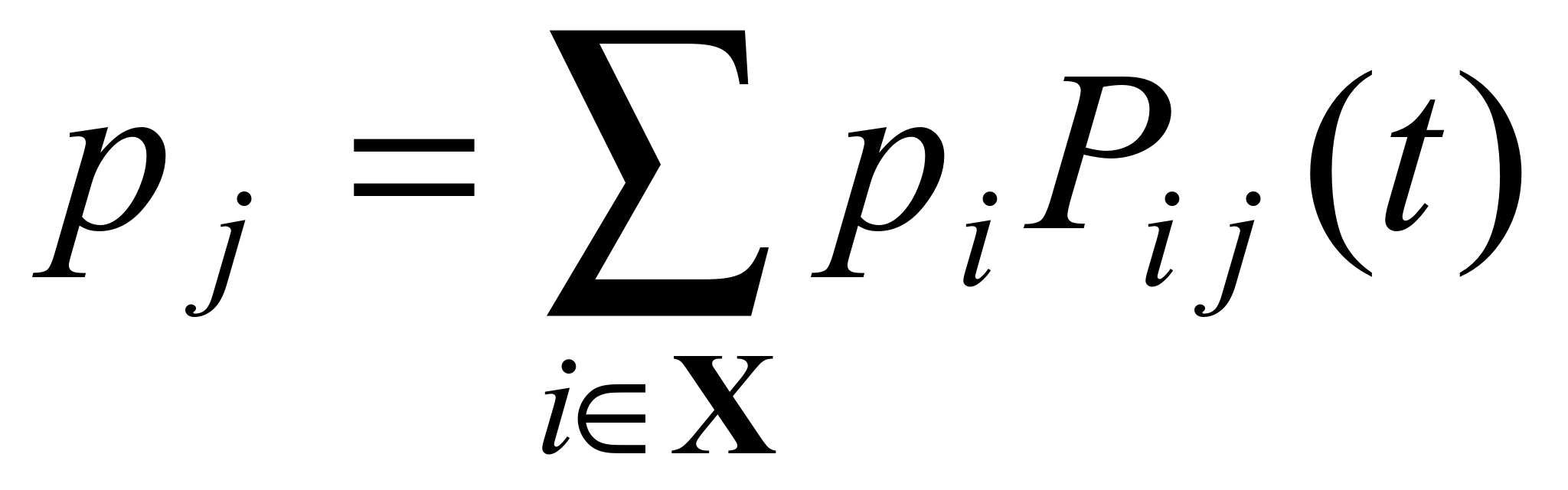 .Если
в произвольный момент времени ЦМ
характеризуется стационарным
распределением, то это означает, что
безусловные вероятности ее состояний
не зависят от времени; такая ЦМ называется
стационарной. В частности, отсюда
следует, что для любой стационарной ЦМ
начальное распределение
.Если
в произвольный момент времени ЦМ
характеризуется стационарным
распределением, то это означает, что
безусловные вероятности ее состояний
не зависят от времени; такая ЦМ называется
стационарной. В частности, отсюда
следует, что для любой стационарной ЦМ
начальное распределение ![]() является
стационарным (т.е.
является
стационарным (т.е. ![]() для
любого
для
любого ![]() ),
поскольку оно удовлетворяет уравнениям,
записанным в определении 2 . Финальные
вероятности состояний системы.
Если процесс, протекающий в системе,
длится достаточно долго, то имеет смысл
говорить о предельном поведении
вероятностей
),
поскольку оно удовлетворяет уравнениям,
записанным в определении 2 . Финальные
вероятности состояний системы.
Если процесс, протекающий в системе,
длится достаточно долго, то имеет смысл
говорить о предельном поведении
вероятностей
![]() при
при
![]() .
В некоторых случаях существуют финальные
(предельные) вероятности состояний:
.
В некоторых случаях существуют финальные
(предельные) вероятности состояний:![]() ,
,
![]() .,
не зависящие от того, в каком состоянии
система находилась в начальный момент.
Говорят, что в системе устанавливается
предельный
стационарный режим,
при котором она переходит из состояния
в состояние, но вероятности состояний
.,
не зависящие от того, в каком состоянии
система находилась в начальный момент.
Говорят, что в системе устанавливается
предельный
стационарный режим,
при котором она переходит из состояния
в состояние, но вероятности состояний
![]() уже не
меняются во времени.
Система, для которой существуют финальные
состояния, называется эргодической,
а соответствующий случайный процесс –
эргодическим.
Финальные вероятности системы могут
быть получены путем решения системы
линейных алгебраических
уравнений, которые получаются из
дифференциальных уравнений Колмогорова,
если приравнять производные к нулю, а
вероятностные функции состояний
уже не
меняются во времени.
Система, для которой существуют финальные
состояния, называется эргодической,
а соответствующий случайный процесс –
эргодическим.
Финальные вероятности системы могут
быть получены путем решения системы
линейных алгебраических
уравнений, которые получаются из
дифференциальных уравнений Колмогорова,
если приравнять производные к нулю, а
вероятностные функции состояний
![]() в правых частях уравнений Колмогорова
заменить на неизвестные финальные
вероятности
в правых частях уравнений Колмогорова
заменить на неизвестные финальные
вероятности
![]() .
Таким образом, для системы с
.
Таким образом, для системы с
![]() состояниями получается система
состояниями получается система
![]() линейных однородных алгебраических
уравнений с
линейных однородных алгебраических
уравнений с
![]() неизвестными
неизвестными
![]() ,
которые можно найти с точностью до
постоянного множителя. Для нахождения
их точных значений к уравнениям добавляют
нормировочное условие
,
которые можно найти с точностью до
постоянного множителя. Для нахождения
их точных значений к уравнениям добавляют
нормировочное условие
![]() ,
пользуясь которым можно выразить любую
из вероятностей через другие и отбросить
одно из уравнений. Рассмотрим пример.
Имеется размеченный граф состояний
системы
,
пользуясь которым можно выразить любую
из вероятностей через другие и отбросить
одно из уравнений. Рассмотрим пример.
Имеется размеченный граф состояний
системы
![]() (рис.2). Необходимо составить систему
дифференциальных уравнений Колмогорова
и записать начальные условия для решения
этой системы, если известно, что в
начальный момент система находилась в
состоянии .
(рис.2). Необходимо составить систему
дифференциальных уравнений Колмогорова
и записать начальные условия для решения
этой системы, если известно, что в
начальный момент система находилась в
состоянии .
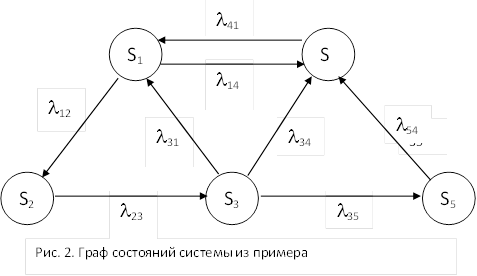 Решение.
Согласно приведенному выше мнемоническому
правилу, система дифференциальных
уравнений Колмогорова имеет вид:
Решение.
Согласно приведенному выше мнемоническому
правилу, система дифференциальных
уравнений Колмогорова имеет вид: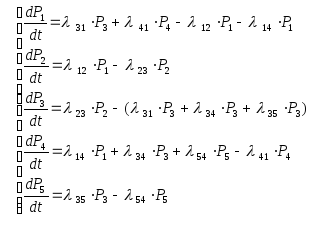 Начальные
условия при
Начальные
условия при
![]() :
:
![]() .
При
.
При
![]() функции
функции
![]() стремятся к предельным (финальным)
вероятностям состояний системы. Поскольку
финальные вероятности не зависят от
времени, в системе дифференциальных
уравнений Колмогорова все левые части
принимаем равными нулю. При этом система
дифференциальных уравнений превратится
в систему линейных алгебраических
уравнений вида:
стремятся к предельным (финальным)
вероятностям состояний системы. Поскольку
финальные вероятности не зависят от
времени, в системе дифференциальных
уравнений Колмогорова все левые части
принимаем равными нулю. При этом система
дифференциальных уравнений превратится
в систему линейных алгебраических
уравнений вида:
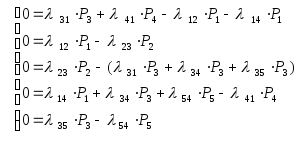 Решая
ее с учетом условия,
Решая
ее с учетом условия,
![]() получим все предельные вероятности.
Эти вероятности представляют собой
среднее
относительное время пребывания системы
в каждом из состояний. Финальные состояния
марковской системы с непрерывным
временем существуют при следующих
условиях: плотности вероятности всех
переходов не должны зависеть от времени
получим все предельные вероятности.
Эти вероятности представляют собой
среднее
относительное время пребывания системы
в каждом из состояний. Финальные состояния
марковской системы с непрерывным
временем существуют при следующих
условиях: плотности вероятности всех
переходов не должны зависеть от времени
![]() ;
из любого состояния системы возможен
переход в любое другое состояние за
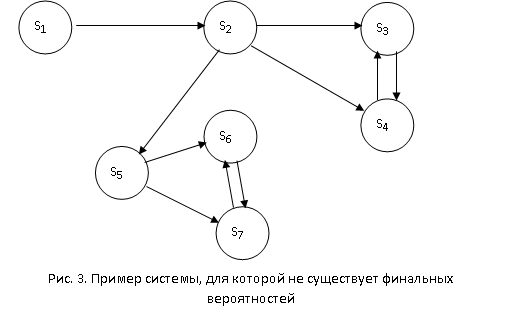
конечное число шагов. Например, для
системы, изображенной на рис. 3, финальные
вероятности не существуют. В заключение
рассмотрим одну из наиболее простых и
часто встречающихся на практике
разновидностей дискретных марковских
цепей с непрерывным временем – так
называемую схему
гибели и размножения.
;
из любого состояния системы возможен
переход в любое другое состояние за
конечное число шагов. Например, для
системы, изображенной на рис. 3, финальные
вероятности не существуют. В заключение
рассмотрим одну из наиболее простых и
часто встречающихся на практике
разновидностей дискретных марковских
цепей с непрерывным временем – так
называемую схему
гибели и размножения.
35.
Процессы гибели и размножения. Во
многих системах, в которых функционирует
СП, возникают ситуации, когда из любого
(кроме первого и последнего) состояния
Si возможен переход только в соседние
состояния Si+1 и Si-1. такие процессы
называются процессами гибели и размножения
и они описываются графом состояний.
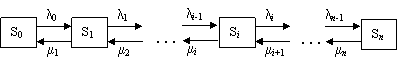
Интенсивности
(лямбда) называются интенсивностями
размножения, а mi
– интенсивности гибели. Для нахождения
вероятности каждого состояния используются
формулы:
 ,
,
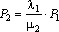 Например:
Организация
принимает заявки от населения на
проведение ремонтных работ. Заявки
принимаются по телефону, по двум линиям
и их обслуживают два диспетчера. Если
одна линия занята, заявка автоматически
переключается на вторую. Если обе линии
заняты – заявка теряется. Среднее число
обслуживания одной заявки – 6 минут. В
среднем одна заявка приносит прибыль
в 30 рублей. Какова прибыль за час? Введем
возможные состояния:
S0
– нет заявок (оба телефона свободны),
S1 – одна заявка обслуживается (один
телефон занят),S2 – две заявки обслуживаются
(оба телефона заняты).
Граф
состояний будет иметь вид:
Например:
Организация
принимает заявки от населения на
проведение ремонтных работ. Заявки
принимаются по телефону, по двум линиям
и их обслуживают два диспетчера. Если
одна линия занята, заявка автоматически
переключается на вторую. Если обе линии
заняты – заявка теряется. Среднее число
обслуживания одной заявки – 6 минут. В
среднем одна заявка приносит прибыль
в 30 рублей. Какова прибыль за час? Введем
возможные состояния:
S0
– нет заявок (оба телефона свободны),
S1 – одна заявка обслуживается (один
телефон занят),S2 – две заявки обслуживаются
(оба телефона заняты).
Граф
состояний будет иметь вид:![]() Находим
вероятности состояний. По приведенным
формулам:
Находим
вероятности состояний. По приведенным
формулам:![]() В
среднем, за час теряется 54% заявок или
0,54 ×30 = 16,2 заявки. Обслуживается 13,8 заявок
в час и средняя прибыль 13,8 ×30 = 414 рублей.
В
среднем, за час теряется 54% заявок или
0,54 ×30 = 16,2 заявки. Обслуживается 13,8 заявок
в час и средняя прибыль 13,8 ×30 = 414 рублей.
///// это уже не то!
25. При исследовании операций часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении однотипных задач. Возникающие при этом процессы получили название процессов обслуживания, а системы – систем массового обслуживания (СМО). Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны – обслуживаемая и обслуживающая. Примерами процессов этого типа являются: 1)обслуживание покупателей в сфере розничной торговли; 2)транспортное обслуживание; 3)медицинское обслуживание населения; 4)ремонт аппаратуры, машин, механизмов, находящихся в эксплуатации; 5)обработка документов в системе управления; 6)туристическое обслуживание. Неотъемлемой частью системы массового обслуживания является узел обслуживания, через который осуществляется взаимодействие входного и выходного потоков заявок. В случае транспортного обслуживания каналом может считаться отдельная единица транспортного средства. Вид графической модели зависит как от числа каналов n, так и от допустимой длины очереди m. По числу обслуживающих каналов различают одноканальные и многоканальные СМО. Находящиеся в СМО заявки могут либо ожидать обслуживания, либо находиться под обслуживанием. Часть заявок, ожидающих обслуживания, образует очередь. В зависимости от целочисленного значения m используются следующие названия в классификации типов СМО: 1)m = 0 – без очереди; 2) m > 0 – с очередью. Если число мест в очереди m является конечным, то в СМО могут происходить отказы в предоставлении обслуживания некоторым заявкам. В связи с этим СМО указанного типа называются системами с отказами. Отклоняются от обслуживания те заявки, в момент прихода которых все места в очереди случайно оказались занятыми, или, если m = 0, все каналы оказались занятыми. Считается, что заявка, получившая отказ в обслуживании, навсегда теряется для СМО. Таким образом, пропускная способность СМО этого типа всегда меньше 100 %. Если m не ограничено, что иногда условно записывают как m = , то соответствующая СМО называется системой с ожиданием. В СМО данного типа пришедшая заявка при отсутствии возможности немедленного обслуживания ожидает обслуживания, какой бы длинной ни были очередь и продолжительность времени ожидания. Одноканальная, без очереди-0, Многоканальная, без очереди n > 1 , Одноканальная, с ограниченной очередью 1 < m <∞; n > 1, 1 < m <∞ Многоканальная, с ограниченной очередью; 1,m = ∞ Одноканальная, с неограниченной очередью; n > 1,m = ∞ Многоканальная, с неограниченной очередью.
26. Мат статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений. Первая задача мат статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений. Вторая задача мат статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть: - оценка неизвестной вероятности события; - оценка параметров распределения случайной величины; -оценка неизвестной функции распределения случайной величины; -проверка гипотез о параметрах распределения или о виде неизвестного распределения; -оценка зависимости случайной величины от одной или нескольких случайных величин и т.д. Статистика - это одна из общественных наук, имеющая целью сбор, анализ, упорядочивание и сопоставление числового представления фактов, относящихся к самым разнообразным массовым явлениям. Статистич наблюдение - первая стадия статистического исследования, представляющего собой научно-организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни. Статистич наблюдение может быть осуществлено посредством отчетности и посредством специально организованных обследований. Это – основные организационные формы статистич наблюдения. В российской статистике используются 3 основные организационные формы статистического наблюдения: -статистическая отчетность (предприятий, организаций, учреждений и т. п.); -специально организованное статистическое наблюдение (переписи, единовременные учеты и обследования); -регистры.
27.Статистическая
гипотеза и общая схема ее проверки.
Статистической
гипотезой называется любое предположение
о виде или параметрах неизвестного
закона распределения. Различают простую
и сложную статистич гипотезы. Простая
гипотеза полностью определяет
теоретическую функцию распределения
случайной величины. Например, гипотезы
«вероятность появления события в схеме
Бернулли равна 1/2», «закон распределения
случайной величины нормальный с
параметрами а = 0, σ2 = 1» являются простыми,
а гипотезы «вероятность появления
события в схеме Бернулли заключена
между 0,3 и 0,6», «закон распределения не
является нормальным» —- сложными.
Проверяемую гипотезу обычно называют
нулевой (или основной) и обозначают H0.
Наряду с нулевой гипотезой H0
рассматривают альтернативную, или
конкурирующую, гипотезу Н1, являющуюся
логическим отрицанием H0.
Нулевая и альтернативная гипотезы
представляют собой две возможности
выбора, осуществляемого в задачах
проверки статистических гипотез. Суть
проверки статистической гипотезы
заключается в том, что используется
специально составленная выборочная
характеристика (статистика)
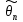 (X1…Xn),
полученная по выборке X1…,Xn,
точное или приближенное распределение
которой известно. Затем по этому
выборочному распределению определяется
критическое значение θкр — такое, что
если гипотеза H0
верна, то вероятность P(
(X1…Xn),
полученная по выборке X1…,Xn,
точное или приближенное распределение
которой известно. Затем по этому
выборочному распределению определяется
критическое значение θкр — такое, что
если гипотеза H0
верна, то вероятность P(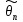 >θкр)
= альфа, а мала; так что в соответствии
с принципом практической уверенности
в условиях данного исследования событие
>θкр)
= альфа, а мала; так что в соответствии
с принципом практической уверенности
в условиях данного исследования событие
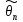 >θкр можно (с некоторым риском) считать
практически невозможным. Поэтому, если
в данном конкретном случае обнаруживается
отклонение
>θкр можно (с некоторым риском) считать
практически невозможным. Поэтому, если
в данном конкретном случае обнаруживается
отклонение
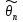 >θкр то гипотеза H0
отвергается, в то время как появление
значения
>θкр то гипотеза H0
отвергается, в то время как появление
значения
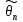 ≤ θкр считается совместимым с гипотезой
H0,
которая тогда принимается (точнее, не
отвергается). Правило,
по которому гипотеза H0
отвергается или принимается, называется
статистическим критерием или
статистическим тестом.
≤ θкр считается совместимым с гипотезой
H0,
которая тогда принимается (точнее, не
отвергается). Правило,
по которому гипотеза H0
отвергается или принимается, называется
статистическим критерием или
статистическим тестом.
28.
Проверка гипотезы о мат ожидании случ
величины при известной и не известной
её дисперсии. Пусть
мы имеем выборку ![]() случайных
величин, распределенных по нормальному
закону
случайных
величин, распределенных по нормальному
закону ![]() .
В этом случае задачи проверки гипотез
о мат ожиданиях и дисперсиях формулируются
следующим образом. 1. В критерии проверки
гипотез вида
.
В этом случае задачи проверки гипотез
о мат ожиданиях и дисперсиях формулируются
следующим образом. 1. В критерии проверки
гипотез вида ![]() при
известной дисперсии
при
известной дисперсии ![]() используется
статистика
используется
статистика 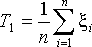 ,
которая при справедливости
гипотезы
,
которая при справедливости
гипотезы ![]() подчиняется
нормальному распределению:
подчиняется
нормальному распределению: 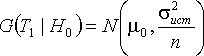 .
Проверяемая гипотеза
.
Проверяемая гипотеза ![]() отклоняется
при больших отклонениях
отклоняется
при больших отклонениях ![]() от
от ![]() .
2. Для проверки гипотезы
.
2. Для проверки гипотезы ![]() при
неизвестной дисперсии
при
неизвестной дисперсии ![]() используется
статистика
используется
статистика 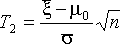 ,где
,где ,
,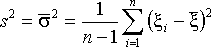 При справедливости
При справедливости
статистика ![]() распределена
как
распределена
как ![]() –
распределение Стьюдента.
–
распределение Стьюдента.
30.Проверка гипотезы о дисперсии сл. величины. (Как известно Дисперсия хар-ет рассеивание относит-но матем.ожидания,хар-ет ошибки некторого процесса в кот.присутствует некоторая сл.величина.) При проверке гипотезы по Дисперсии H0 формир.в виде: H0 : Gx2= G02, H1 : Gx2> G02, H1 : Gx2 < G02, H1 : Gx2 ≠ G02
G02 -гипотетич.Дисепрсия сл.величин. В качестве выбор.ф-ции для проверки гипотезы: Z=Gx2 (n-1)/ G02
Gx2 –несмещенная оценка Дисп, ; n-объем выборки. Как правило чаще всего в качестве в качестве альт.гипотезы зад.гипотеза вида: H1 : Gx2> G02. Если справедлива H0 ,то дан.выбор.ф-ция имеет χ2 распределения с числом степеней свободы (n-1). Поэтому по ур-нию значимости α по табл. χ2 распр-я опр-ся . критич.обл. При этом если критич.обл.правостор, то знач.критич.обл.опр..из условия: P(Z >Zкр ) = α . Рез-ты статич.набл предстваляет выбор-ф-цию,если получ. рез-т принадлежит критич.обл, то H0отклон,а принимается альтернативная (H1)
31.Проверка гипотезы о равенстве дисперсий сл. величии.1)Проверка по 2м сл.величинам:H0 : Gx2= Gy2 H1 : Gx2> Gy2 H1 : Gx2 < Gy2 H1 : Gx2 ≠ Gy2. По данным стат.наблюд.опр-ся несмещенная оценка Дисп/ для вел.X и Y соот-но (Gx2 Gy2) . А в качестве выбор.ф-ции для проверки этой гипотезы зад-ся выр: Z= Gx2/ Gy2(1) при этом берется отношение большего значения несмещенной оценки Дисперсии к меньшей.,т.е предполагают,что Gx2>Gy2. Если справедлива H0,то дан.выбор.ф-ция им.F-распр-е (распр-е Филлера) с числом степеней свободы : K1= nx -1 ; K2 = ny -1, nx ny –объем выборки для X и Y соот-но По ур-нию знач α, виду альт.гипотезы, по табл.F-распр-я для заданного числа степени свободы опр-ся критич.обл.. Рез-ты стат. набл. подставл. в выбор.ф-цию. Если получ. рез-т попадает в критич.обл.,то H0отклоняется, и приним.альт.реш(H1), 2)Проверка гипотезы по сов-сти сл.вел: H0: G12 = G22 =…= G n2. Расм.2 случая, когда объем выборки для разл.сл.величин X1,X2 ,..,Xm различен (n1≠ n2 ≠ nm). В этом случае проверка H0 осущ. по критерию Бартлетта. Если объем выборки для всех сл.величин одинаков n1= n2 =nm,,то H0 м.проверить по критерию k-члена. В качестве выбор.ф-ции зад.выражение: Z= Gmax2 / G12 + G22 +…+ Gm2 ,Gmax2- max несмещенная оценка Дисперсии. G12 G22 Gm2 –несмещенные оценки Дисперсии соотв-но для вел X1,X2 ,..,Xm Если справедлива H0 гипотеза,то данная выбор.ф-ция им.распр-е k-члена,зависящее от объема выборки n и числа исслед.велич.m. По ур-нию знач. α По табл распр-я k-члена опр-ся критич.обл,получ-е оценки Дисперсии G12 G22 Gm2 и Gmax2подставл. В выбор ф-цию ,если получ.рез-т принадлежит критич.обл,то H0 отклоняется и применяется альт. гипотеза.
32.Проверка гипотезы о числовом значении вероятности события и гипотезы о равенстве вероятности двух событий. H0 :P= P0 ; H1 :P> P0 ; H1 : P< P0 ; H1: P ≠ P0. По дан.стат.набл.опр-ся P* пояления соб.в отдельном опыте/ A в качестве выбор.ф-ции зад.выр вида: Z= P* - P0 / корень (P0 (1- P0) /n). Дан. выбор. ф-ция при достаточно большом числе испытаний им.стандартное нормюраспр-е ,если справедлива H0 Поэтому по ур-нию значимости α ,виду альт.гипотезы опр-ся кр.обл. по табл стандарного распр-я. Рез-ты наблюдений и гипотетич.вер-сть подставляется в выборочную ф-цию. Если получ. рез-т принадлежит Кр.обл,то H0 отклоняется.
