
terver
.docx33.Проверка гипотезы о законе распр. сл величины по критерию ХИ-квадрат X1,X2 ,..,Xn. По этим рез-там надо проверить гипотезу о з.распр-я сл.вел.Для проверки этой гипотезы формир. H0 : F(x)= F0 (x) и альт.гипотезы H1 : F(x)> F0 (x) ; H1 : F(x) < F0 (x)H1 : F(x) ≠ F0 (x). F0 (x)-гипотетич.ф-ция распр.сл.вел. Проверку дан.гипотезы м/осущ-ть по разл.критериям: Критерию Колмогорова,По критерию ω2,По критерию χ2
Проверка гипотезы про критерию χ2 по раср-ии дискр.сл.вел..Пусть дискр.сл.вел.X приним.значения X1,X2 ,..,Xm ,где m-число возм.знач.сл.вел. Оно м/б конечным и бесконечным. Обознач.через ki (i=1,2..e) число тех наблюдений, кот-е в рез-те опыта принимали знач. ki. Очевидно, что с ростом Vвыборки стат.вер-сть б/стремиться в теоретич.
Lim ki /n= P0(X=Xi) (1)
n∞ При усл,что H0 :P= P0 справедливо H1 :P> P0 ; H1 : P< P0 ; H1: P ≠ P0.При проверке дан.гипотезы зад.выр.вида: Z=∑ [ki - P0(X=Xi)n ]2/ P0(X=Xi)n (2)
i=1, l-число разл.знач. сл.величины, кот-е были получены в рез-те опыта. P0(X=Xi)n = niT(3) наз.теоретич.частотой. Дан.выборор.ф-ция имеет χ2 распр-я с числом степеней свободы K=l-1-r
r-число параметров гипотетич. распр-я, кот-е оценивались по рез-там статич. наблюдений.
Проверка гипотезы о з.распределения непрерывной сл.величины. При проверке этой гипотезы по Крит. χ2 по дан.стат. наблюдений составл.табл..частот:
|
Част.интерв. |
(x0 - x1 )
|
x1 - x 2
|
… |
(xi-1 - x1 )
|
…. |
x k-1 - x k
|
|
niC
|
n1C
|
n2C
|
…. |
niC
|
… |
nkC
|
|
niT
|
n1T
|
n2T
|
… |
niT
|
… |
nkT
|
niC –cтат.частота, niT-теоретич.частота, теоретич.частота,соотв.частотного инетрвала: niT= n(F0 (xi) - F0 (xi-1) )
F0 –гипотетич.ф-ция распр-я. В качестве выбор.ф-ции для проверки этой гипотезы зад.выр.вида:
k
Z=∑ (niC- niT)2/ niT
i=1. Если справедлива H0 : F(x)= F0 (x) ,то дан.выб.ф-ция имеет χ2 распр-я с числом степеней свободы l=k-1-r, k-число част.интервалов ; r-число параметров гипотетич.ф-ции рапср-я ,кот-е оценивались по рез-ту стат.набл.,если они были неизвестны. По заданным ур-нию α и виду альт.гипотезы опр-ся кр.обл.по табл χ2 распр-я.. Рез-ты наблюдений и теоретич.подставл.в выбор.ф-ции ,если получ.рез-т принадлежит кр.обл,то H0 отклоняется.
34
Проверка гипотезы об однородности двух
выборок.
При
проверке этой гипотезы формир-ся 2
выборки из 2-х генер.совок-тей.
По
этим данным проверяется H0
гипотеза:
X1,X2
,..,Xn
Y1,Y2
,..,Yn,
H0
:
F(x)=
F(y),
H1
:
F(x)>
F(y),
H1
:
F(x)
< F(y),H1
: F(x)
≠ F(y)
Дан.гипотеза
м/б проверить по 2м критериям,по критерию
Смирнова и критерию Вилконсона.
Наиб.проще
реализовать критерий Вилксона при
проверке данной гипотезы.
По
данным рез-там набл.формируется вариац.ряд
независимо от того какой величине
принадлежит рез-т наблюдения.
Вариационный
ряд в порядке возрастания.
|
X1 |
X2 |
Y3 |
X4 |
Y5 |
… |
Yn+m+1 |
Xn+m |
|
1 |
2 |
3 |
…. |
5 |
… |
n +m+1 |
n+m |
|
|
|
3 |
… |
5 |
… |
n +m+1 |
|
Во 2ю строку табл..записаны цифры одного из вар-ов перестановочной комбинации из чисел (n+m)! Предполаг.что число набл.над сл.вел. Y m=< n над сл.вел. X. 3ю строку записывают числа 2строки кот-е нах-ся под рез-ми набл.над сл.вел Y. В качестве выборочной ф-ции зад.выраж.вида: Z=∑ ri , ri –знач.чисел находящихся в 3й строке табл. Док-ся,что выбор.ф-ция имеет распр-е Вилконсона,характерезующая объемом выборки n и m. В дальнейшем по ур-нию значимости α по таблицам Вилконсона для заданного числа набл. n и m опр-ся критич.обл. по ур-нию значимости и виду альт.гипотезы следует иметь виду,что табл.Вильконсона составляется для левосторонней критич.обл. Если необходимо опр.правостор.кр.обл,то табл.в начале опр. Не левостор.кр.обл,а правостор.кр.обл. Zкр.пр.=m(n +m+1- Zкр.л.). Если 2х стор.кр.обл,то по табл.для ур-ния значимости α/2. Zкр.л. опр-ют,а затем опр-ют Zкр.пр По данным табл.опр.реализ.выбор.ф-ции. Если рез-т принадл.кр.обл,то H0 отклон. При Vвыборки n>25 дан. гипотеза м/б проверена по табл.станд.норм.распределения,то выбор.ф-ция им.норм.распр-е: mz =m(m+n+1)-1/2
Gz2 =m*n(m+n+1)/2 И тогда кр.обл для заданного уровня значимости по таблицам норм.распр-я опр-ся критич.точка. Критич.обл.соот-но опр-ся по формуле: Zкр.л. = mz± α/2 Gz2
35. Статистическая оценка характеристик (параметров случайной величины) Оценка характеристик случайной величины проводится, когда знания числовых характеристик случайной величины достаточно для определения их основных свойств. Оценки бывают: 1)точечные, 2)интервальные (доверительные).-точечная – при ней не делается заключение о точности и надёжности оценки характеристики случайной величины; -при доверительной оценке указывается точность и надёжность данной оценки. Если неизвестны характеристики случайной величины, то их оценка осуществляется по результатам статистических наблюдений. При этом заранее неизвестно, какие это будут результаты. Поэтому каждый из результатов наблюдений рассматривается как случайная величина с характеристиками, соответствующими характеристикам исследуемой случайной величины.
36. Точечная оценка параметров распределения. Точечная оценка предполагает нахождение единственной числовой величины, которая и принимается за значение параметра. Такую оценку целесообразно определять в тех случаях, когда объем ЭД достаточно велик. Причем не существует единого понятия о достаточном объеме ЭД, его значение зависит от вида оцениваемого параметра. При малом объеме ЭД точечные оценки могут значительно отличаться от истинных значений параметров, что делает их непригодными для использования. Задача точечной оценки параметров в типовом варианте постановки состоит в следующем. Имеется: выборка наблюдений (x1, x2, …, xn) за случайной величиной Х. Объем выборки n фиксирован. Известен вид закона распределения величины Х, например, в форме плотности распределения f(T, x), где T – неизвестный (в общем случае векторный) параметр распределения. Параметр является неслучайной величиной. Требуется найти оценку q параметра T закона распределения. Ограничения: выборка представительная. Существует несколько методов решения задачи точечной оценки параметров, наиболее употребительными из них являются методы максимального (наибольшего) правдоподобия, моментов и квантилей. Метод максимального правдоподобия предложен Р. Фишером. Основан на исследовании вероятности получения выборки наблюдений (x1, x2, …, xn). Эта вероятность равна f(х1, T) f(х2, T) … f(хп, T) dx1 dx2 … dxn. Совместная плотность вероятности L(х1, х2 …, хn ; T) = f(х1, T) f(х2, T) … f(хn, T), рассматриваемая как функция параметра T, называется функцией правдоподобия. В качестве оценки q параметра T следует взять то значение, которое обращает функцию правдоподобия в максимум. Для нахождения оценки необходимо заменить в функции правдоподобия Т на q и решить уравнение L/ q = 0. В целях упрощения вычислений переходят от функции правдоподобия к ее логарифму ln L. Такое преобразование допустимо, так как функция правдоподобия – положительная функция, и она достигает максимума в той же точке, что и ее логарифм. Если параметр распределения векторная величина q =(q 1, q 2, …, q n), то оценки максимального правдоподобия находят из системы уравнений: ln L(q 1, q 2, …, q n) / q 1 = 0; ln L(q 1, q 2, …, q n) / q 2 = 0; . . ln L(q 1, q 2, …, q n) / q n = 0. Для проверки того, что точка оптимума соответствует максимуму функции правдоподобия, необходимо найти вторую производную от этой функции. И если вторая производная в точке оптимума отрицательна, то найденные значения параметров максимизируют функцию. Нахождение оценок максимального правдоподобия включает следующие этапы: 1)построение функции правдоподобия (натурального логарифма); 2)дифференцирование функции по искомым параметрам и составление системы уравнений; 3)решение системы уравнений для нахождения оценок; 4)определение второй производной функции, проверку ее знака в точке оптимума первой производной и формирование выводов. Метод максимального правдоподобия позволяет получить состоятельные, эффективные (если таковые существуют, то полученное решение даст эффективные оценки), достаточные, нормально распределенные оценки. Этот метод может давать как смещенные, так и несмещенные оценки. Смещение удается устранить введением поправок. Метод особенно полезен при малых выборках. Оценка инвариантна относительно преобразования параметра, т.е. оценка некоторой функции j (Т) от параметра Т является эта же функция от оценки j (q ). Если функция максимального правдоподобия имеет несколько максимумов, то из них выбирают глобальный.Метод моментов предложен К. Пирсоном в 1894 г. Сущность метода: выбирается столько эмпирических моментов, сколько требуется оценить неизвестных параметров распределения. Желательно применять моменты младших порядков, так как погрешности вычисления оценок резко возрастают с увеличением порядка момента; вычисленные по ЭД оценки моментов приравниваются к теоретическим моментам; параметры распределения определяются через моменты, и составляются уравнения, выражающие зависимость параметров от моментов, в результате получается система уравнений. Решение системы дает оценки параметров распределения генеральной совокупности. Метод моментов позволяет получить состоятельные, достаточные оценки, они при довольно общих условиях распределены асимптотически нормально. Смещение удается устранить введением поправок. Эффективность оценок невысокая, т.е. даже при больших объемах выборок дисперсия оценок относительно велика (за исключением нормального распределения, для которого метод моментов дает эффективные оценки). В реализации метод моментов проще метода максимального правдоподобия. Метод целесообразно применять для оценки не более чем четырех параметров, так как точность выборочных моментов резко падает с увеличением их порядка.
37.Доверительная оценка характеристик случайной величины. Ранее рассматривалась точечная оценка характеристик случайной величины. При этой оценке не делается заключение о точности и надёжности. Ответы на эти вопросы даёт доверительная оценка характеристик случайной величины. Пусть для некоторого параметра (характеристики) случайной величины проводится несмещённая оценка, которая удовлетворяет всем требованиям, предъявляемым к оценкам. Требуется определить возможную ошибку. Т.е. насколько будет отличаться оценка от оцениваемого параметра. Для решения задачи задаётся доверительная вероятность, при этом значение вероятности таково, что событие, которое может произойти с этой вероятностью, можно считать достоверным. С надёжностью действительное значение параметра будет находиться в указанном интервале. Любая оценка проводится по результатам статистических наблюдений. Данная оценка проводится при известном распределении выборочной функции (статистики). Она связывает результаты статистических наблюдений и неизвестный параметр. На практике чаще всего проводится доверительная оценка для математического ожидания, дисперсии и вероятности события. При решении этих задач основными распределениями являются: нормальное распределение; хи-квадрат распределение; распределение Стьюдента.
38Доверительная оценка математического ожидания и дисперсии случайной величины Доверительный интервал для математического ожидания нормальной случайной величины при известной дисперсии. Пусть количественный признак X генеральной совокупности имеет нормальное распределение с заданной дисперсией у2 и неизвестным математическим ожиданием M(Х~N(т, у)). Построим доверительный интервал для т. 1) Пусть для оценки т извлечена выборка х1, х2, ..., хп объема n. Тогда 2) Составим случайную величину . Нетрудно показать, что случайная величина u имеет стандартизированное нормальное распределение, т.е. u~N(0,1) . 3) Зададим уровень значимости б. 4)Применяя формулу нахождения вероятности отклонения нормальной величины от математического ожидания, имеем: (3). Это означает, что доверительный интервал накрывает неизвестный параметр т с надежностью 1- б. Точность оценки определяется величиной [6]. Отметим, что число определяется по таблице значений функции Лапласа из равенства [2]. Пример 1. На основе продолжительных наблюдений за весом X пакетов орешков, заполняемых автоматически, установлено, что стандартное отклонение веса пакетов у = 10 г. Взвешено 25 пакетов, при этом их средний вес составил = 244 г. В каком интервале с надежностью 95 % лежит истинное значение среднего веса пакетов? Логично считать, что случайная величина X имеет нормальный закон распределения: Х~N(m, 10). Для определения 95%-го доверительного интервала найдем критическую точку = u0,025 из приложения 1 по соотношению. Тогда по формуле (3) построим доверительный интервал. Доверительный интервал для математического ожидания нормальной случайной величины при неизвестной дисперсии. В реальности истинное значение дисперсии исследуемой случайной величины, скорее всего, известно не будет. Это приводит к необходимости использования другой формулы при определении доверительного интервала для математического ожидания случайной величины, имеющей нормальное распределение. Пусть X ~ N(m, у2), причем т и у2 -- неизвестны. Необходимо построить доверительный интервал, накрывающий с надежностью г = 1 - б истинное значение параметра т. Для этого из генеральной совокупности случайной величины X извлекается выборка объема п: х1, х2, ..., хп. 1. В качестве точечной оценки математического ожидания т используется выборочное среднее , а в качестве оценки, дисперсии у2 -- исправленная выборочная дисперсия , которой соответствует стандартное отклонение . 2. Для нахождения доверительного интервала строится статистика , имеющая в этом случае распределение Стьюдента с числом степеней свободы v = п - 1 независимо от значений параметров т и у 2., 3. Задается требуемый уровень значимости б.,4. Применяется следующая формула расчета вероятности(4) где -- критическая точка распределения Стьюдента, которая находится по соответствующей таблице. Тогда Это означает, что интервал накрывает неизвестный параметр m с надежностью 1 - б. Пример 2. Найти доверительный интервал для оценки неизвестного математического ожидания нормально распределенного признака, если известны: у = 2; = 5, 4; n = 10; г = 0,95.
40.Выборочное
корреляционное отношение. Эмпирическое
корреляционное отношение X
по Y.
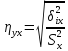 .Отметим основные свойства корреляционных
отношений
(при достаточно большом объеме выборки
n):
1.
Корреляционное отношение есть
неотрицательная величина, не превосходящая
1: 0≤ η≤ 1. 2. Если η = 0 , то корреляционная
связь отсутствует.
3.
Если η = 1, то между переменными существует
функциональная зависимость.
4.
ηyx
≠
ηxy
т.е. в отличие от коэффициента корреляции
r
(для которого ryx
= rxy
= r)
при вычислении корреляционного отношения
существенно, какую переменную считать
независимой, а какую — зависимой.
Эмпирическое
корреляционное отношение
ηyx
,
является показателем рассеяния точек
корреляционного поля относительно
эмпирической линии регрессии, выражаемой
ломаной, соединяющей значения уi
.Однако в связи с тем, что закономерное
изменение уi
нарушается случайными зигзагами ломаной,
возникающими вследствие остаточного
действия неучтенных факторов, ηyx
преувеличивает
тесноту связи. Поэтому наряду с ηyx
рассматривается
показатель тесноты связи Ryx
,характеризующий рассеяние точек
корреляционного поля относительно
линии регрессии уx
.Показатель Ryx
получил
название теоретического корреляционного
отношения или индекса корреляции Y по
X:
.Отметим основные свойства корреляционных
отношений
(при достаточно большом объеме выборки
n):
1.
Корреляционное отношение есть
неотрицательная величина, не превосходящая
1: 0≤ η≤ 1. 2. Если η = 0 , то корреляционная
связь отсутствует.
3.
Если η = 1, то между переменными существует
функциональная зависимость.
4.
ηyx
≠
ηxy
т.е. в отличие от коэффициента корреляции
r
(для которого ryx
= rxy
= r)
при вычислении корреляционного отношения
существенно, какую переменную считать
независимой, а какую — зависимой.
Эмпирическое
корреляционное отношение
ηyx
,
является показателем рассеяния точек
корреляционного поля относительно
эмпирической линии регрессии, выражаемой
ломаной, соединяющей значения уi
.Однако в связи с тем, что закономерное
изменение уi
нарушается случайными зигзагами ломаной,
возникающими вследствие остаточного
действия неучтенных факторов, ηyx
преувеличивает
тесноту связи. Поэтому наряду с ηyx
рассматривается
показатель тесноты связи Ryx
,характеризующий рассеяние точек
корреляционного поля относительно
линии регрессии уx
.Показатель Ryx
получил
название теоретического корреляционного
отношения или индекса корреляции Y по
X:
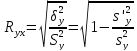
41. Проверка зависимости (независимости) случайных величин Т.к. степень силы связи между случайными величинами, входящими в систему, определяется коэффициентом кореляции, то при определении независимости случайными величинами, входящими в систему, формируется гипотеза вида: Где rxy - коэффициент кореляции между случайными величинами X или Y. В качестве выборочной функции при проверке этой гипотезы задаётся выражение вида: Где - статист коэффициент кореляции. При справедливости нулевой гипотезы данная выборочная функция имеет распределение с числом степеней свободы , поэтому нулевая гипотеза проверяется по таблицам распределения. Если не подтверждается гипотеза о независимости случ величин, то может быть сформулирована гипотеза о силе связи между случайными величинами, входящими в систему: ,,, Данная гипотеза проверяется по выборочной функции вида: где - статистич коэффициент корреляции. Если справедлива нулевая гипотеза, то данная выборочная функция имеет стандартное нормальное распределение с характеристиками: /\ Чтобы нулевую гипотезу можно было проверить по таблицам нормального стандартного распределения, переходят к нормированным и центрированным выборочным функциям: - (4). Она имеет нормальное стандартное распределение. Поэтому нулевую гипотезу проверяют с помощью таблиц стандартного нормального распределения, т.е. по уровню значимости и виду альтернативной гипотезы определяют критическую область, а по выборочной функции (4) определяют её реализацию. Если полученный результат попадает в критическую область, то нулевая гипотеза отклоняется.
43.Основные
положения регрессионного анализа.
Определение ур-я линии регрессии методом
наименьших квадратов.
?/Корреляционно-регрессионный
характер.
Важной хар-ой системы СВ явл связь между
СВ, вход в систему, связь определяется
с помощью уравнений, ур-е регрессии и
др. Корреляционно-регрессионные отношения
разделяются на парные и множественные.
Если рассматривается система из 2х СВ,
то анализ называется парным. Если система
из 3х и более систем СВ, то анализ
называется множественным.
Проверка
гипотезы при парном анализе. Эта
гипотеза проверяется по результатам
стат.наблюдений над системой 2х СВ. Если
проверяется гипотеза об отсутствии
корреляционной связи между СВ, то она
формируется в связи между отсутст.СВ и
формируется гипотеза вида:
H₁: =0;
H₁:
=0;
H₁: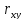 >0;
H₁:
>0;
H₁: <0;
H₁:
<0;
H₁: ≠0.
По данным стат.наблюдений определяется
выборочный коэф.корреляции:
≠0.
По данным стат.наблюдений определяется
выборочный коэф.корреляции:
 ,
и задается: Z=
,
и задается: Z= .
По ур-ю значения α, по виду альтернативного
распределения определяется критич.обл.,
по данным стат.наблюдений определяется
значение выборочной ф-ции. При проверки
по коррелированности СВ формируется
гипотеза вида: H₀:
.
По ур-ю значения α, по виду альтернативного
распределения определяется критич.обл.,
по данным стат.наблюдений определяется
значение выборочной ф-ции. При проверки
по коррелированности СВ формируется
гипотеза вида: H₀: =r₀;
H₀:
=r₀;
H₀: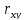 >r₀;
H₀:
>r₀;
H₀: <r₀;
H₀:
<r₀;
H₀: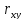 ≠r₀.
В качестве выборочной функции задается
z=
≠r₀.
В качестве выборочной функции задается
z=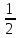 ln
ln (1). Дан.выборочная ф-ция имеет нормальное
распределение матем.ожидания: m₂=
(1). Дан.выборочная ф-ция имеет нормальное
распределение матем.ожидания: m₂= ln
ln
 (2),
(2),
 =
= (3).
Для того, чтобы данную гипотезу можно
было проверить по табл.стандартного
распределения задается:
(3).
Для того, чтобы данную гипотезу можно
было проверить по табл.стандартного
распределения задается:
 =
= (4). Если справедлива ф-ция, то (4) имеет
стандартное нормальное распределение.
По ур-ю значения α, виду альтернативной
гипотезы, по табл.стандартного
распределения определяется критич.
обл. По данным стат. наблюдения определяется
реализация (4) функции. Если получится
результат принадлежащий критич.обл, то
0-я гипотеза отклоняется.
Уравнение
линии регрессии определяется методом
наим.квадратов
по данным статистич.наблюдениям. Пусть
имеются статистические наблюдения над
системой СВ, указанных на графике,
который отражает характеристику одной
СВ от зависимости др.СВ.
(4). Если справедлива ф-ция, то (4) имеет
стандартное нормальное распределение.
По ур-ю значения α, виду альтернативной
гипотезы, по табл.стандартного
распределения определяется критич.
обл. По данным стат. наблюдения определяется
реализация (4) функции. Если получится
результат принадлежащий критич.обл, то
0-я гипотеза отклоняется.
Уравнение
линии регрессии определяется методом
наим.квадратов
по данным статистич.наблюдениям. Пусть
имеются статистические наблюдения над
системой СВ, указанных на графике,
который отражает характеристику одной
СВ от зависимости др.СВ.

 .
Сумма квадратов должна быть минимизирована.
Эта линия может задаваться в виде
различных ф-ций: в виде прямой, многочлена
и т.д. Чаще всего эта линия представляет
собой уравнение прямой линии. Ур-ние ее
определяется методом наименьш. квадратов.
А и В –некоторые коэффициенты. Ȳ/x=A+BX
(1), φ(A,B)=
.
Сумма квадратов должна быть минимизирована.
Эта линия может задаваться в виде
различных ф-ций: в виде прямой, многочлена
и т.д. Чаще всего эта линия представляет
собой уравнение прямой линии. Ур-ние ее
определяется методом наименьш. квадратов.
А и В –некоторые коэффициенты. Ȳ/x=A+BX
(1), φ(A,B)= -(A+
-(A+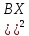 =min
(2),
=min
(2),
 ,
,
 - минимизированные ф-ции. Минимизирование
ф-ций 2х переменных будет в 1ой точке,
где частные производные = 0, т.е. для
нахождения коэф.А и В, удовлетворяющие
этому условию, составляем систему
уравнения:
- минимизированные ф-ции. Минимизирование
ф-ций 2х переменных будет в 1ой точке,
где частные производные = 0, т.е. для
нахождения коэф.А и В, удовлетворяющие
этому условию, составляем систему
уравнения:
 =
= =0,
=0,
 =
= =0
(3). Если мы решим эту систему, то коэф-ты
А и Б будут выражаться через результаты
статист наблюдений. Док-ся, что ур-е (1),
выражается через результаты статист.
наблюдений, имеет вид: Y/x=Ȳ+
=0
(3). Если мы решим эту систему, то коэф-ты
А и Б будут выражаться через результаты
статист наблюдений. Док-ся, что ур-е (1),
выражается через результаты статист.
наблюдений, имеет вид: Y/x=Ȳ+ (x-x̄)
(4),
(x-x̄)
(4),
 -статистический
коэффициент корреляции.
-статистический
коэффициент корреляции.
 ,
,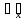 -статистическое среднее квадратическое
отклонение для СВ Х и У. Аналогичным
образом док-ся, что уравнение линии
регрессии для Х имеет вид: X̄/y=x̄+
-статистическое среднее квадратическое
отклонение для СВ Х и У. Аналогичным
образом док-ся, что уравнение линии
регрессии для Х имеет вид: X̄/y=x̄+ (y-ȳ)
(5). 44.Однофакторный
дисперсионный анализ. Однофакторная
дисперсионная модель имеет вид: Xiy
= μ
+ Fi
+ Ɛiy
, где
Хiy
— значение исследуемой переменной,
полученной на i-м
уровне
фактора (i=1,2,...,m)
с j-м
порядковым номером (j=1,2,...,n);
Fi
— эффект, обусловленный влиянием i-го
уровня фактора;
Ɛiy
— случайная компонента, или возмущение,
вызванное влиянием неконтролируемых
факторов, т.е. вариацией переменной
внутри отдельного уровня. Под уровнем
фактора понимается некоторая его мера
или состояние, например, количество
вносимых удобрений, вид плавки металла
или номер партии деталей и т.п. Основные
предпосылки дисперсионного анализа:
1.
Мат ожидание возмущения Ɛiy
равно нулю для любых i,
т.е. M(Ɛiy)
= 0.
2.
Возмущения Ɛiy
взаимно независимы. 3. Дисперсия возмущения
Ɛiy
(или переменной Xiy)
постоянна для любых I,j,
т.е. D(Ɛiy)
= σ2
. 4. Возмущение Ɛiy
(или переменная Xiy)
имеет нормальный закон распределения
N(0;
σ2)
(y-ȳ)
(5). 44.Однофакторный
дисперсионный анализ. Однофакторная
дисперсионная модель имеет вид: Xiy
= μ
+ Fi
+ Ɛiy
, где
Хiy
— значение исследуемой переменной,
полученной на i-м
уровне
фактора (i=1,2,...,m)
с j-м
порядковым номером (j=1,2,...,n);
Fi
— эффект, обусловленный влиянием i-го
уровня фактора;
Ɛiy
— случайная компонента, или возмущение,
вызванное влиянием неконтролируемых
факторов, т.е. вариацией переменной
внутри отдельного уровня. Под уровнем
фактора понимается некоторая его мера
или состояние, например, количество
вносимых удобрений, вид плавки металла
или номер партии деталей и т.п. Основные
предпосылки дисперсионного анализа:
1.
Мат ожидание возмущения Ɛiy
равно нулю для любых i,
т.е. M(Ɛiy)
= 0.
2.
Возмущения Ɛiy
взаимно независимы. 3. Дисперсия возмущения
Ɛiy
(или переменной Xiy)
постоянна для любых I,j,
т.е. D(Ɛiy)
= σ2
. 4. Возмущение Ɛiy
(или переменная Xiy)
имеет нормальный закон распределения
N(0;
σ2)
45.Общие сведения о временных рядах и задачах их анализах. Анализ временных рядов представляет собой самостоятельную, весьма обширную и одну из наиболее интенсивно развивающихся областей математической статистики. Под временным рядом (динамическим рядом, или рядом динамики) в экономике подразумевается последовательность наблюдений над экономическим процессом, в последовательные равностоящие моменты времени. При исследовании этого ряда выделяются несколько составляющих результатов наблюдений в момент времени t: xt = ut + vt + сt + Ɛt (t = 1,2,...,n), где u — тренд, плавно меняющаяся компонента, vt — сезонная компонента, отражающая некую повторяемость экономических процессов,ct—циклическая компонента, отражает закономерност экономических процессов. Et— случайная компонента, отражает неучтенные случайные факторы. Следует обратить внимание на то, что в отличие от Ɛt первые три составляющие (компоненты) ut , vt , ct , являются закономерными, неслучайными. Важнейшей классической задачей при исследовании экономических временных рядов является выявление и статистическая оценка основной тенденции развития изучаемого процесса и отклонений от нее. Отметим основные этапы анализа временных рядов: • графическое представление и описание поведения временного ряда; • выделение и удаление закономерных (неслучайных) составляющих временного ряда ; • сглаживание и фильтрация (удаление низко- или высокочастотных составляющих временного ряда); • исследование случайной составляющей временного ряда, • прогнозирование развития изучаемого процесса на основе имеющегося временного ряда; • исследование взаимосвязи между различными временными рядами.
