А сколькими вариантами можно составить группы из двух равноправных дежурных?

Задача 2. Следствие ведут знатоки.

В городе Стукове происходят два ЧП в день. На место происшествия отправляют оперативную группу из трех человек: следователя, оперативника и эксперта. В УВД несут службу 3 следователя, 2 оперативника и 3 эксперта. График их работы составляется таким образом, чтобы каждая очередная опергруппа отличалась от предыдущих (пока это возможно). Трое друзей – следователь Знаков, оперативник Токов и эксперт Кирюшина мечтают почаще работать вместе. Как часто это им удается по графику?

Решение. Построим дерево возможных составов оперативных групп, учитывая что следователя можно выбрать тремя способами (С1, С2, С3), оперативника – двумя (О1 и О2), а эксперта – тремя способами (Э1, Э2 , Э3).

А

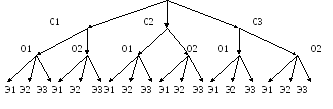
Данный рисунок наглядно показывает, что число различных опергрупп равно 18.

Тот же результат может быть получен на основе рассуждений, аналогичных приведенным в предыдущей задаче.

N = 3 · 2 · 3 =18.

Можно сформулировать правило, применимое к задачам, подобным рассмотренным выше.

Правило умножения. Пусть необходимо выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n₁ способами, после чего второе действие можно выполнить n₂ способами, после чего третье действие можно выполнить n₃ способами, и так далее до k-го действия, которое можно выполнить n_k. способами, то все k. действий вместе могут быть выполнены n₁ · n₂ · n₃ · ... · n_k способами.

Решить самостоятельно задачу. Замок сейфа открывается, если набрана правильная комбинация из четырех цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число неудачных попыток.

2. Размещения, перестановки, сочетания

При решении комбинаторных задач мы имеем дело с комбинациями из некоторых предметов. Эти комбинации могут отличаться одна от другой числом предметов, их составом и порядком.

Пример 1. Пять бойцов сержанта Сбруева.

В отделении сержанта Сбруева проходят службу 5 новобранцев: Белкин, Пенкин, Фенькин, Свечкин и Овечкин. Сколькими способами сержант может построить этих новобранцев в одну шеренгу при занятиях строевой подготовкой?

Решение. Договоримся указывать порядок расположения солдат первыми буквами их фамилий. Например, комбинация ПСОФБ означает, что первым стоит Пенкин, вторым – Свечкин и т. д. Все комбинации отличаются одна от другой порядком букв и называются перестановками из пяти букв. Сформулируем определение и общую формулу, а затем вернемся к примеру.

Определение. Перестановкой из n элементов называется всякий способ нумерации этих элементов.

Число всех различных перестановок из п элементов равно п! (произносится «эн – факториал»). Обозначается Pn.

P_n = п! =1·2·3·…·n

Эту формулу легко доказать на основе правила умножения.

В случае с солдатами число всех возможных перестановок P5 = 5! =1·2·3·4·5=120.

Пример 2. Однажды утром.

Однажды утром по улицам города Дрюкова на высокой скорости пронеслась машина. Она сбила зазевавшегося поросенка и скрылась в неизвестном направлении. Возвращавшийся из ресторана житель N, заметил номер автомобиля. Но к приезду милиции, в силу известных обстоятельств, вспомнил только, что номер четырехзначный, все цифры разные, причем первая цифра 1, а последняя 4. Сколько автомобилей должна проверить автоинспекция?

Решение. Второй и третьей цифрами номера могут быть любые две из следующих цифр: 2, 3, 5, 6, 7, 8, 9, 0. Нужно перебрать столько номеров, сколько будет возможных комбинаций из восьми перечисленных цифр по две с учетом их порядка. Такие комбинации называются размещениями. В данном случае нас интересует число размещений из восьми цифр по две.

Определение. Размещением из n элементов по m называется всякая перестановка из m элементов, выбранных каким-либо способом из данных n. Число размещений из n элементов по m обозначается .

= n · (n-1) · (n-2) ·…· (n-m+1).

Эту формулу легко доказать, используя правило умножения. Каждое размещение можно получить с помощью m действий. Первое действие – выбор первого элемента – осуществляется n способами, второе действие – выбор второго элемента – (n - 1) способами, и т. д., наконец последнее действие – выбор m-го элемента – (n- m -1) способами.

По правилу умножения число всех размещений будет n·(n-1) ·(n-2) ·…· (n-m+1).

В нашем примере =8 · 7 =56.

Эту же формулу можно записать иначе, используя выражение факториала.

Пример 3. День брюквы.

Согласно древнему обычаю, самый главный праздник в Брюкове – День Брюквы, проводится за счет средств городского бюджета и празднуется столько дней, сколько депутатов проголосует за то, чтобы праздник состоялся. Из десяти депутатов «за» проголосовали семь. Каково число всех возможных вариантов голосования?

Решение. Мы должны найти число всех возможных групп из семи депутатов. Здесь порядок выбора не играет никакой роли, поэтому комбинации отличаются одна от другой только составом лиц. Комбинации такого типа называются сочетаниями.

Определение. Сочетанием из n элементов по m называется всякая совокупность m элементов, выбранных каким-либо способом из данных n элементов. Число всех сочетаний из n элементов по m обозначается .

Ту же формулу с использованием факториала можно записать в следующем виде

В нашем примере нужно вычислить .