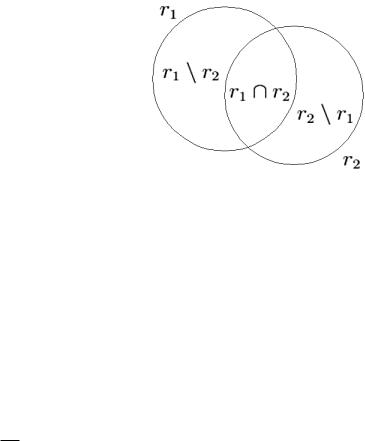
Рис. 2.1.: Круги Эйлера: r1(S) \ r2(S) = r1 n (r1 n r2) = r2 n (r2 n r1)
определение операции внутреннего соединения.
2.6. Пример построения выражения реляционной алгебры
Практическое задание. Имеется следующий фрагмент базы данных:
Поставщики(КодПщ, Имя, Город) Детали(КодД, РодД, ...) Поставки(КодПщ, КодД)
Написать выражение реляционной алгебры, позволяющее получить наименования поставщиков
(Имя) и место их расположения (Город) в случае, когда поставщики не поставляют каких-либо деталей с родовым именем (РодД) 0Болт0. При желании можно применить линейную форму представления запроса в виде набора операторов присваивания.
Решение. По условию задания в отношении Детали могут быть детали с различными кодами КодД, но одним и тем же родовым именем РодД.
Применим линейную форму представления запроса в виде набора операторов присваивания. Образуем естественное соединение всех отношений:
R1 := Поставщики ./ Поставки ./ (Детали[КодД, РодД])
Выборка из отношения R1 по условию РодД = 0Болт0 с последующей проекцией на атрибуты отношения Поставщики позволяет получить список всех Поставщиков, поставляющих хотя бы одну деталь с родовым именем 0Болт0:
R2 := ( hРодД = 0Болт0iR1)[КодПщ, Имя, Город]
Разность отношений Поставщики и R2 дает искомый список Поставщиков. Остается спроектировать результат на заданные атрибуты:
R3:= (Поставщики n R2)[Имя, Город]
Сворачивая цепочку операторов присваивания, получим окончательно искомое выражение реляционной алгебры, реализующее заданный запрос:
(Поставщики n ( hРодД = 0Болт0i
(Поставщики ./ Поставки ./ (Детали[КодД, РодД])
)
)[КодПщ, Имя, Город] )[Имя, Город]
2.7. Понятие базовых и виртуальных отношений
На наиболее абстрактном уровне база данных – это множество отношений D. Замыкая D (обозначение D+) относительно введенных ранее операций реляционной алгебры, получим множество всех отношений (включая сами отношения D), которые можно получить из D, применяя введенные операции. Тем самым получаем реляционную алгебру над множеством отношений базы данных, то есть множество (называемое носителем) с набором операций (называемым алгебра, сигнатура):
hD+; ; ; ; [; \; n; ; ./i
Таким образом, исходя из отношений D, хранимых в базе данных, можно получить в результате запроса отношение не только из D, но и из D+ n D. Но в базе данных хранятся отношения двух видов – базовые (обозначим D0) и виртуальные (обозначим D1). (Ясно, что D0 \ D1 = ;; D0 [ D1 = D). Базовые отношения содержат независимые данные и не могут быть выражены через другие отношения базы данных. В СУБД базовые отношения обычно называются таблицами (table). Виртуальные отношения выражаются в конечном итоге через базовые и (на логическом уровне) хранятся в базе данных в виде выражений реляционной алгебры. В СУБД виртуальные отношения обычно называются представлениями (view). Реально они реализуются на языке SQL.
2.8. Понятие полноты реляционной алгебры
Сигнатура реляционной алгебры, так, как она была введена выше, содержала операции, производные от других операций, и в этом смысле была избыточной. Однако на практике производные операции полезны, так как позволяют в более компактной форме представлять выражения.
Важен другой вопрос: а достаточно ли этих операций для выражения практически значимых запросов? Действительно, если из сигнатуры алгебры исключить операции типа произведения ( и ./), то в результате запроса, формулируемого в виде выражения реляционной алгебры над отношениями базы данных с оставшимися операциями ( ; ; ; [; \; n) могут быть получены результирующие отношения со схемами, с точностью до переименования атрибутов являющимися подмножествами или совпадающими со схемами исходных отношений. Такого ограниченного набора операций для практики явно не достаточно. Возникает вопрос о полноте набора операций реляционной алгебры.
Если проанализировать определения операций реляционной алгебры, то можно заметить, что все они с точностью до обозначений определяются в виде выражений вида «множество кортежей над такой-то схемой, удовлетворяющих такому-то предикату»:
ft(S) j f(t)g
Здесь f – некоторый предикат над переменным кортежем t. Это выражение обозначает отношение r(S), которое состоит из всех кортежей t(S), для которых f(t) истинно.
Можно задаться вопросом, не будут ли получены новые запросы-отношения из базы данных, если в качестве предиката f в таких выражениях использовать произвольный предикат, включающий логические связки 8 (квантор общности, или всеобщности), 9 (квантор существования) и :; &; _ (отрицание, конъюнкция, дизъюнкция)? (Такие выражения с произвольным предикатом f, выраженным в элементарных высказываниях, использованных при определении операций реляционной алгебры, называются выражениями исчисления кортежей.) Можно показать, что нет.