Дать определение погрешности решения, погрешности аппроксимации, аппроксимации и сходимости разностной схемы. Провести исследование аппроксимации и сходимости явной и неявной разностной схемы метода Эйлера.
Пример. Аппроксимирует ли разностная схема
Задачу
Коши (ЗК) 
.
С каким порядком?
Общий
случай:
-
разностная схема, L(u)=0
– непр. задача, y
– точное решение разностной схемы, u
– точное решение ЗК.
Величина
наз
погрешностью
аппроксимации
разностной схемы исх задачи. (Смысл опр:
хотим определить, насколько дискретная
модель отличается от исходной)
Погр аппрокс разностной исх зад на точном решении равна невязке.
Математическое
понятие аппроксимации: Разностная схема
аппроксимирует
исходную задачу, если 
,аппроксимация
порядка P,
если 
(т.е
при бесконечном дроблении сетки арг
)
Для метода Эйлера p=1
Уст разностной схемы
Запишем
Разностная
схема устойчива,
если
,
не зависящие от h
и выбора u_0
и f,
что им место нер-во 
а)
если 
,
а 
,
то имеет место 
;
б) 
,
то имеет место уст по правой части 
Если
шаг 
то
– уст по начальным
данным.
Если
шаг 
(
),
то условная
устойчивость.
Всё сказанное справедливо и для систем ДУ, только вместо абс вел-ны ставим норму.
Сходимость разностных схем и погрешность.
Теорема:
Пусть исх зад z(u)=0
пост корр-но и разн схема
аппроксимирует
разн схему с пар-ом 
,
h
→ 0. И пусть разн сх уст, тогда разн сх
сх-ся, т.е 
h
→ 0. Причем сх-ся с порядком = погрешности
аппрокс-ии 
Док-во:
подставим
в разн сх метода Эйлера:
Из
усл. устойч.: и на основании леммы (из
уст. по нач. данным след. уст. по пр. части)
и 
(*)
.
С другой стороны р.сх. также аппрокс.
решение, т.е. 
с порядком р 
.
(В случае разн. сх. Эйлера р=1).
Замечание:1.
Из сходимости разн сх => что мы можем
получить решение с любой наперед заданной
точностью. Она будет достигнута
соответствующим дроблением сетки
аргумента; 2. Из полученной оценки
погрешности (*) =>что порядок погрешности
носит суммарный
или глобальный
характер. Поэтому 
будем
рассматривать как глобальную погрешность.
Разн сх является корректно заданной, если она аппрокс уст и сх-ся. Разн сх Эйлера условно уст (шаг выбирают из условия – оценка правой части). Нужно выбирать маленький шаг, чтобы если функция решения сильно изменится, не изменилась правая часть на большую величину.
Пример:
да аппроксимирует с порядком p=1.
(т.к. это р.сх. Эйлера, а для нее доказано,
что погрешность аппроксимации 
).
3. Определить локальную и глобальную погрешность решения задачи Коши разностным методом. Провести построение метода Рунге получения апостериорной погрешности решения. Как используется метод Рунге для автоматического выбора шага сетки аргумента.
Сходимость разностных схем и погрешность.
Теорема: Пусть исх зад L(u)=0 пост корр-но и разн схема аппроксимирует разн схему с пар-ом , h → 0. И пусть разн сх уст, тогда разн сх сх-ся, т.е h → 0. Причем сх-ся с порядком = погрешности аппрокс-ии
Док-во: подставим в разн сх метода Эйлера:
Нашли,
что усл устойчиво: 
и
на основании леммы, что правая часть
уст
(*)
из
условия теоремы об устойчивости: т.к
аппрокспорядка р, то 
,
в случае разн сх Эйлера р=1.
Замечание:1. Из сходимости разн сх => что мы можем получить решение с любой наперед заданной точностью. Она будет достигнута соответствующим дроблением сетки аргумента; 2. Из полученной оценки погрешности (*) =>что порядок погрешности носит суммарный или глобальный характер. Поэтому будем рассматривать как глобальную погрешность.
Разн
сх является корректно
заданной, если
она аппрокс уст и сх-ся. Разн сх Эйлера
условно уст (шаг выбирают из условия
– оценка правой части). Нужно выбирать
маленький шаг, чтобы если функция решения
сильно изменится, не изменилась правая
часть на большую величину.
Построение разностной схемы с переменным шагом h.
Введём понятие локальной погрешности.
Опр. Погрешность локальная (на шаге)
определяется так: 
- получение
конечного решения разностной схемы с
точным начальным условием.
Для м. Эйлера: 
Проведём исследование локальной погрешности в виде порядка малости шага h.
Пусть 
Представим локальную погрешность используя формулу Тейлора (на шаге):
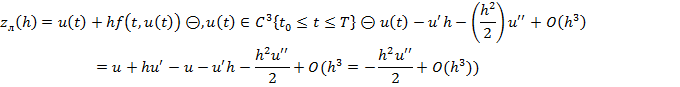
Обобщим для метода
порядка 
Опр. 
называется главным членом локальной
погрешности. 
называется избыточной гладкостью
решения (т.к для оценки погрешности
нужно брать 
степеней
,
а тут 
).
Правило или метод Рунге.
Н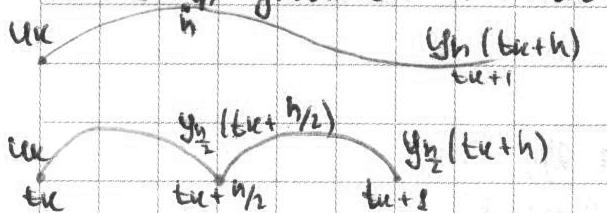
а
отрезке длиной h
с н.у. 
Чтобы исп. формулы
для получения практического решения
нужно из оценки исключить неизвестную
величину 
.
Из 2 вычитаем 1: 
- мы м. получить её реально при вычислениях
и оценить локальную погрешность.
На основании этого
строится схема вычисления локальной
погрешности на каждом шаге, если задана
точность 
и после вычисления величин окажется,
что 
,
тогда применим автоматический выбор
шага.
Автоматический выбор шага.
Используется для получения заданной точности решения в каждой точке аргумента.
Это адаптивная (самонастраиваемая) процедура.
Если 
При каких-то 
.
Получим 
и решение дальше, но функция меняется
и шаг может быть не экономичен, тогда
мы удваиваем шаг. И если получаем, что
не изменяем.
Пример. Привести
алгоритм автоматического выбора шага
аргумента при решении методом Эйлера
задачи Коши 
Запишем разностную схему:
.
Пусть 
Тогда согласно
методу Рунге считаем на каждой итерации
один раз с шагом h
и два раза с шагом h/2.
Затем берем разность полученных значений
как оценку погрешности (надо делить на
– для метода Эйлера p=1,
т.е. делить не нужно). Примерный алгоритм
автоматического выбора шага:
1) 
;
2) 
.
.
Если 
то 
и повторяем шаг. Если 
,
то 
и переходим к следующей итерации. В
противном случае переходим на следующую
итерацию, не меняя шаг.
.
3) 
.
.
.......................................................
И продолжаем цикл
до тех пор, пока не найдем значения в
точке 7 (пока 
).
4.Провести построение разностной схемы Рунге-Кутта с погрешностью аппроксимации 2-го порядка точности.
Пример. Построить такую разностную схему с точностью аппроксимации 10-3 для задачи
Ответ:
Рассмотрим задачу Коши для ДУ: 
Интегрируем уравнение на очень малом
шаге 
:
По формуле левых прямоугольников: 
Если 
то получим: 
Можно использовать: 
.
Тогда замена будет 
В этом случае надо решать нелинейное
уравнение 
для нахождения 
.
Это нелинейное уравнение – решать
методом Ньютона (например) 
эта
формула неэкономична.
Тогда будем решать: 
– формула одношаговая, т.к. для нахождения
последующего значения нужно знать одно
предыдущее; формула явная (т.к. нет
нелинейных уравнений) и здесь 
- выбираются таким образом, чтобы
совокупность этих формул давала
погрешность аппроксимации 2-го порядка
малости по h и
чтобы разн. схема сходилась по h
и была устойчивой.
Найдем 
.
Заметим, что 
.
Разностную схему представим в следующем виде:
Вспомним, что погрешность аппроксимации = невязке разностной схемы на точном решении:
Стандартный прием – разложение в ряд всех точных решений, встреч. в этой записи.
Пусть 
.
Тогда 
:
а) 
-ограниченные
величины, поэтому порядок малости 
.
б) представим по формуле Тейлора 
Подставим а), б) в выражение погрешности аппроксимации:
1) 
,
тогда погрешность аппроксимации будет
второго порядка малости
– формула Рунге-Кутта 2-го порядка. Она
2-х этапная, одношаговая, явная:
Данная формула также называется «предиктор-корректор».
2) 
–формула Рунге-Кутта, одношаговая,
явная 2-х этапная.
Итак, теперь 
,
а из того, что 
следует, что 
и разностная схема аппроксимирует
исходную задачу с порядком h.
Пример. Построим такую разностную схему с точностью аппроксимации 10-3 для задачи
Так как 
,
то 
.
В нашем случае 
.
5. Исследовать устойчивость разностной схемы Рунге-Кутта 2 порядка. Доказать теорему сходимости разностной схемы.
Теорема. Пусть исходная задача z(u)=0 пост. корректно и разн.сх. Lh(y)=0 аппроксимирует разн.сх. с п-ом ψh(u)=O(hp): lim ψh(u)=0 (h->0)/ и пусть разн.сх. устойчива, тогда разн.сх. сх-ся, т.е. сущ-ет lim |yh-uh| =0 (h->0). Причем сх-ся с порядком равным порядку погрешности аппроксимации (u – точное решение исх.з.Коши, y – точное решение разн.сх.) zh = |yh-uh| = O(hp)
Док-во. yh = zh + uh подставим в разн.сх.м.Эйлера: (zk+1 – zk)/h = f(tk, uk + zk) - (uk+1 – uk)/h
f(tk, uk + zk) = f(tk, uk ) + f(tk, uk + θzk) zk
(zk+1 – zk)/h = f(tk, uk) - (uk+1 – uk)/h + α(tk, uk) zk
(zk+1 – zk)/h = α(tk, zk) + ψh(uk), y0-u0=z0, k=0, .., n-1, tk ∈ ωn
(zk+1 – zk)/h = -λ zk +| ψh|
|zk+1| ≤ |1-λh| | zk| + h| ψh(uk)|, т.к. исслед.ист и нашли, что усл.уст-ти: h ≤ 2/λ, | fh(tk, uk + zk)| ≤ λ и на осн.леммы, что пр.часть уст.: | zk| ≤ h| ψh(u0)| + h| ψh(u1)| + … + h| ψh(un-1)|
Т.к. y0
= u0:
| zk|
≤ 
(*)
| zk|
≤ 
- из усл.теоремы об уст-ти: т.к. аппрокс.
порядка р, то сущ-ет lim
|zh|=0
(h->0),
|zk|>O(hp).
в сл.разн.сх.Эйлера р=1.
Замечание: 1. Из сх=ти разн.сх. => что мы можем получить решение с любой наперед заданной точностью. Она будет достигнута соответственным дроблением сетки аргументов.
2. Из получения оценки погрешности (*) следует, что погр-ть носит суммарный или глобальный характер. Поэтому zk будем рассм-ть как глоб.погр-ть.
zh = yh – uh, yh – точное решение, uh – точное решение на сетке аргументов. Тогда используем: (yk+1 – yk)/h = f(tk + h/2, yk + (h/2)f(tk, yk)). Замена: yh = zh + uh, тогда (zk+1 – zk)/h = f(tk + h/2, zk + uk + (h/2)f(tk, zk + uk)).
Приведем уравнение к удобному виду для исследования устойчивости по лин.модели
а) f(tk, zk + uk) представим по ф-ле Лагранжа:
f(tk, zk + uk) = f(tk, uk) + fu(tk, uk + θ1zk)zk = /* fu(tk, uk + θ1zk) = βk */ = f(tk, uk) + βk zk
б) f(tk + h/2, uk + (h/2)f(tk, uk) + zk + (h/2)βk zk) = /* uk + (h/2)f(tk, uk) = ũk, zk + (h/2)βk zk = žk */ = f(tk + h/2, ũk + žk)
Представим эту функцию по ф-ле Лагранжа:
f(tk + h/2, ũk) + fu(t + h/2k, ũk + θ2 žk) žk
(zk+1 – zk)/h = f(tk + h/2, uk + (h/2)f(tk, uk)) – (uk+1 – uk)/h + γk(1 + (h/2) βk)zk = γk(1 + (h/2) βk)zk + ψh(uk), т.о., если мы заменим | γk | ≤ λ, | βk | ≤ λ и будем иметь в виду, что γk , βk ≤ 0, то мы образуем линейную модель разностной схемы в виде:
zk+1 = (1 + γkh(1 + (h/2) βk))zk + hψh(uk) – заменим лин.моделью
zk+1 = (1 - λh(1 - (h/2) λ))zk + hψh(uk) – модельная задача для исследования устойчивости
|zk| ≤ |z0| + M2max| ψh(uj)|, (0≤j≤N-1).
Чтобы получить уст-ть по нач.данным при М=1 и, след-но, уст-ть по правой части, сделаем
|1 – λh(1 – λh/2)| ≤ 1
В случае – λh( 1 – λh/2) < 0 взять др.часть нер-ва в опр. абс.величины: 1 – λh/2 ≥0 => h ≤ 2/λ
Метод Рунге-Кутта 2-го порядка обладает условной уст-тью. По теореме (из аппр. 2-го порядка и из уст-ти => сх-ть разностной схемы)
Сущ-ет lim zh=0, h->0, если z0=0, z0=y0 – u0.
Т.о., доказана корр-ть разностного метода Рунге-Кутта 2-го порядка.
Пример. Построить разностную схему метода Рунге-Кутта 2-го порядка, определив параметр а, при котором имеет место сходимость для задачи Коши. Точность решения ε=0,001.
u’(x) = x2 – au2(x), u(0) = 0, 0<x≤1.
.
В нашем случае
.
u' = f(x, y) = x2 – au2(x)
|fu(x, y)| ≤ λ => |-2au| ≤ λ
u ≤ ||u||
λ = 2a||u||
h ≤ 2/λ, h = 0.03 =>
0.03 ≤ 2/(2|a| ||u||)
|a| ≤ 1/ (0.03||u||) – a, при которых имеет место сх-ть з.Коши
6. Многошаговые методы решения задачи коши характеризуются тем, что решение в текущем виде зависит от данных не в одном предыдущем узле, а в нескольких.
Задача
коши для скалярного уравнения 
- Формула Ньютона-Котеса, интегрального
типа, с постоянным расстоянием между
узлами.
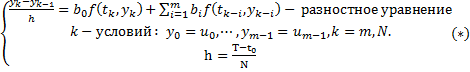
Определение.
Разностная схема (*) называется m
– шаговой разностной схемой Адамса.
Если 
,
то она явная; если 
,
то неявная.
Особенности:
1)Для
получения следующего значения 
надо решить нелинейную задачу :
– неявная разносная схема.
2) До
решения методом Адамса надо знать 
– приближенные значения решения в к-ой
точке.
3)Необходимо
знать функцию в m первых
точках 
Дальше,
при 
надо к каждому следующему прибавлять
только 1 предыдущий :
.
Построить такую схему, значит найти коэффициенты в известном условии аппроксимации, а потом исследовать устойчивость, и если она окажется условной то найти необходимое условие.
Двухшаговый метод Адамса(явный).
.
Предположим, что 
Погрешность аппроксимации на точках
решений = невязке разносной схемы на
точном решении, т.е. 
по формуле Тейлора: 
. Надо получить 2 порядка малости по 
.
Следовательно,
таким образом
она аппроксимирует исходную задачу:
возьмем
.
Задача.
- точное решение разностной схемы.
X(t ) – точное решение исходной задачи Коши.
-
по формуле Лагранжа. Тогда исход задачи
Коши: 
.
А разностная схема, тогда должна выглядеть
так при подстановке в нее.
У нас 
по условию =0, таким образом разностная
схема аппроксимирует исходную задачи
коши с 
,
то есть с первым порядком точности.
