
Nonlinear resonance
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Нижегородский государственный университет им. Н.И. Лобачевского
А.И. Малышев
Избранные главы теории нелинейных колебаний: резонансная теория возмущений
Учебно-методическое пособие
Рекомендовано методической комиссией физического факультета для студентов ННГУ, обучающихся по направлению 011200 «Физика»
Нижний Новгород
2012
УДК 530.182 ББК В 22.213+22.311
М20
М20 Малышев А.И. ИЗБРАННЫЕ ГЛАВЫ ТЕОРИИ НЕЛИНЕЙНЫХ КОЛЕБАНИЙ: РЕЗОНАНСНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ: учебно-методическое пособие. – Нижний Новгород: Нижегородский госуниверситет, 2012. – 21 с.
Рецензент:
доцент кафедры теории колебаний и автоматического регулирования ННГУ, к.ф.-м.н. Канаков О.И.
В настоящем пособии представлен материал по теме «Резонансная теория возмущений», входящей в учебный курс «Нелинейные колебания и волны», читаемый на физическом факультете ННГУ. Кроме необходимых теоретических выкладок, связанных с понятием нелинейного резонанса и перекрытием резонансов, представлен материал практического характера, содержащий, в частности, сопоставление с результатами численного моделирования.
УДК 530.182
ББК В 22.213+22.311
© Нижегородский государственный университет им. Н.И. Лобачевского, 2012
Резонансная теория возмущений
Введение
Как известно, каноническая теория возмущений в случае числа степеней свободы, большего единицы, не работает вблизи резонансов, т.е. в областях, где
m ω I 0 ,
где ω I – вектор невозмущенных частот системы, являющихся, как правило, функ-
циями вектора действия I , а m – вектор с целочисленными компонентами. Нерабо-
тоспособность теории оказывается связанной с тем, что ввиду малости скалярного
произведения m ω I ряды последовательных приближений теории начинают расходиться. Это означает, что адекватное описание поведения системы вблизи резонанса требует отдельного рассмотрения и построения резонансной теории возмущений. Этому вопросу и посвящено настоящее пособие.
- 3 -

Малышев А.И.
I. Резонанс связи двух степеней свободы
Выполним пример построения резонансной теории возмущений для системы с двумя степенями свободы, чей гамильтониан в переменных действие-угол имеет следующий вид:
H I1 ,I2 ,θ1 ,θ2 H0 I1 ,I2 εV I1 ,I2 ,θ1 ,θ2 . |
(1) |
Здесь H0(I1, I2) – гамильтониан невозмущенной системы, а второе слагаемое описывает возмущение, малость которого определяется параметром ε. Невозмущенные частоты колебаний определяются известным образом:
ω |
H0 |
. |
(2) |
|
|||
1,2 |
I1,2 |
|
|
|
|
||
Рассмотрим подробнее резонанс |
|
|
|
nω1 – mω2 = 0, |
(3) |
||
где n и m – положительные целые числа. Поскольку речь идет о резонансе между колебаниями по двум разным степеням свободы в замкнутой системе, такой резонанс еще называют внутренним резонансом или резонансом связи. Заметим также, что последнее равенство может быть записано в виде скалярного произведения векторов
|
,ω2 |
|
ω ω1 |
и m n, m . |
|
Поскольку на резонансе разность nω1 – mω2 равна нулю, то вблизи резонанса |
||
разность nθ1 – mθ2 является медленной функцией времени по сравнению, например, с θ1(t) и θ2(t). Используем это – совершим каноническое преобразование посредством производящей функции
откуда
|
|
mJ |
|
nJ |
|
I |
1 |
||||
|
1 |
|
2 |
|
|
|
|
nJ1 mJ2 |
|||
I2 |
|||||
F |
m |
θ1 nθ2 |
|
J |
nθ1 mθ2 |
J |
, |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
n2 m2 |
1 |
|
n2 |
m2 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
mψ nψ |
|||||
|
n |
2 |
m |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
θ |
||||||||
|
|
|
|
|
|
|
|
|
и 1 |
|
1 |
2 |
||||
|
|
2 |
|
|
2 |
|
|
nψ1 mψ2 |
||||||||
|
n |
m |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
θ2 |
||||||||

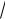 n2 m2
n2 m2 
 n2 m2
n2 m2
(4)
(5)
Легко заметить, что такое каноническое преобразование соответствует повороту системы координат в плоскостях частот (ω1, ω2) и действий (I1, I2) (см. рис. 1). Таким образом, новыми угловыми переменными становятся быстрая фаза
ψ1 |
|
|
mθ1 |
nθ2 |
(6) |
|||||
|
|
|
|
|
|
|
|
|||
|
|
n2 |
m2 |
|||||||
|
|
|
|
|
||||||
и медленная фаза |
|
|
|
|
|
|
|
|
|
|
ψ |
nθ1 |
mθ2 |
. |
(7) |
||||||
|
|
|
|
|||||||
2 |
|
|
|
n2 |
m2 |
|
||||
|
|
|
|
|
||||||
- 4 -

Резонансная теория возмущений
Рис. 1. Иллюстрация к каноническому преобразованию (5)
Прежде, чем перейти в гамильтониане к новым переменным, заметим следующее. Функция возмущения, вообще говоря, является периодической функцией переменных θ1 и θ2, поэтому может быть разложена в двойной ряд Фурье:
V I1 ,I2 ,θ1 ,θ2 |
Vn ,m I1 ,I2 ei n θ1 m θ2 . |
(8) |
|
n ,m 0 |
|
При этом для простоты положили, что среднее значение возмущения равно нулю. Если это не так, то возможны два варианта – либо среднее значение является функцией только переменных действия, либо оно является константой. В первом случае слагаемое V0,0 I1 ,I2 может быть включено в невозмущенную часть гамильтониана, что
приведет к небольшому изменению невозмущенных частот (2), которое может быть описано в рамках канонической теории возмущений. Во втором случае, постоянная составляющая гамильтониана может быть вовсе исключена.
Таким образом, гамильтониан (1) приобретает следующий вид:
H H0 J1 , J2 ε |
Vn ,m J1 , J2 e |
i |
n mψ1 nψ2 m nψ1 mψ2 |
|
|
||||
|
|
|
|
|
|
|
|||
|
|
n2 |
m2 |
. |
(9) |
||||
|
|
|
|
|
|
||||
n ,m 0
Усредним его по быстрой фазе ψ1, в результате получим:
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||
|
|
H0 J1 , J2 ε V |
m J1 , J2 ei |
|
|
n |
m |
ψ2 , |
(10) |
|
|
|
n |
||||||||
H |
||||||||||
|
|
n 0 n , n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||
а также оставим в сумме по n׳ самые медленные слагаемые – с n׳ = ±n:
|
|
|
|
J , J |
εV |
J , J |
ei |
|
|
|
J , J |
e i |
|
|
|
|
|
H |
|
n2 m2 ψ2 |
εV |
n2 m2 ψ2 . |
(11) |
||||||||
H |
0 |
||||||||||||||
|
|
|
1 2 |
n, m |
1 2 |
|
|
|
n,m |
1 2 |
|
|
|
|
|
Обе оставшиеся гармоники обычно примерно равны друг другу, поэтому положим далее для простоты1
V |
J , J |
|
V |
J |
, J |
|
|
V0 J1 , J2 |
. |
(12) |
2 |
2 |
|
||||||||
n, m |
1 |
n,m |
1 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||
1Замечание, касающееся этого равенства, будет сделано в заключение настоящего раздела.
-5 -

Малышев А.И.
В результате гамильтониан (11) примет вид: |
cos |
|
|
|
. |
|
|||||||||||||||
|
|
|
|
J , J |
|
|
|
|
J , J |
|
|
|
|
|
|
||||||
|
|
|
H |
|
|
εV |
|
|
n2 m2 ψ |
(13) |
|||||||||||
H |
0 |
2 |
2 |
||||||||||||||||||
|
|
|
|
|
1 |
|
|
0 |
1 |
|
|
2 |
|
||||||||
Из канонических уравнений, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(14) |
|
|
|
|
|
J , J |
|
n2 |
m2 |
sin n2 m2 ψ |
|
||||||||||||
J |
εV |
2 |
ε, |
|
|||||||||||||||||
2 |
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
следует, что J1(t) = J10 = const, а J2(t) меняется мало, на величину порядка ε. Это позво-
ляет сделать в гамильтониан подстановку J10 вместо J1, и |
~ |
t вместо J2, а также |
J20 J |
произвести разложение его слагаемых в ряд Тейлора с точностью до первого неисче-
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
зающего порядка по J : |
|
|
|
|
|
|
|
|
εV0 J10 , J20 cos |
|
|
|
|
|
. |
|
||
|
|
|
|
H0 |
~ |
|
1 |
2H0 ~2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||
H H0 J10 , J20 |
|
|
|
m |
ψ2 |
|
||||||||||||
J2 |
J |
|
J2 |
2 |
J |
n |
|
|
(15) |
|||||||||
2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь необходимо заметить, что значения J10 и J20 отвечают области резонанса и определяются в соответствии с (5) резонансными значениями действий I1R и I2R. В результате второе слагаемое в правой части последнего соотношения оказывается равным нулю:
H0 |
|
0 . |
(16) |
J2 |
ψ2 |
||
J1 J10 , |
|
|
|
|
J2 J20 |
|
|
Первое же слагаемое может быть исключено из гамильтониана как постоянная. Обо-
значая далее вторую производную 2H |
J2 |
|
|
|
|
|
за K, получим резонансный га- |
||||||
|
|
|
|
0 |
2 |
J1 J10 ,J2 J20 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
мильтониан (гамильтониан эффективно одномерной системы): |
|
||||||||||||
|
|
K |
~2 |
εV0 cos |
|
|
|
|
|
ψ2 |
|
|
|
|
Hres |
|
|
2 |
m |
2 |
|
|
|||||
|
|
J |
|
n |
|
|
|
(17) |
|||||
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Легко видеть, что это есть гамильтониан математического маятника, что открывает возможность найти основные параметры резонанса, такие как ширина и частота малых колебаний.
Для расчета ширины резонанса необходимо получить уравнение его сепаратрисы – кривой, отделяющей траектории, попавшие в резонанс, от траекторий возмущенных, но не попавших в резонанс. Применительно к математическому маятнику сепаратрисой является кривая, разделяющая в фазовой плоскости области с колебательным и вращательным режимами движения; на рис. 2 она показана красным цветом. Итак, положим энергию системы равной максимальной потенциальной энергии, т.е. εV0, тогда
|
|
|
εV cos |
|
|
|
|
ψ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 m2 |
|
|
|
|||||
|
K |
~2 |
|
|
|
|
|
~ |
|
|
εV |
|
|
|
|
||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||||||||
εV |
|
m |
|
2 |
0 |
|
|
|
|
ψ2 |
|
|
|||||||||
|
J |
n |
|
|
J |
|
|
cos |
|
|
|
|
(18) |
||||||||
|
|
|
|
|
|
|
|||||||||||||||
0 |
2 |
|
0 |
|
|
|
|
2 |
|
|
|
|
K |
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда ширина резонанса:
|
|
|
|
|
|
|
|
~ |
|
|
εV0 |
|
|
|
|
J |
4 |
|
|
|
(19) |
||
K |
|||||||
|
|
|
|
|
|
||
- 6 -
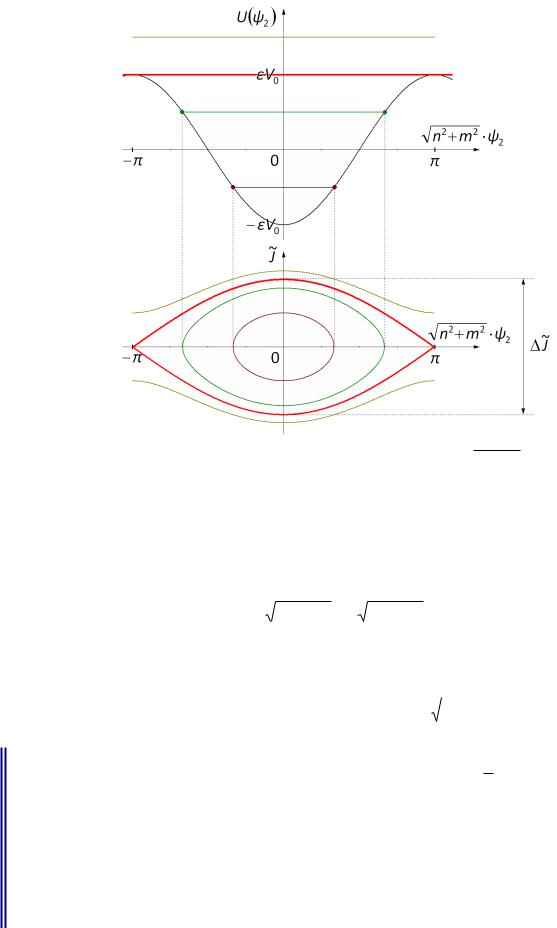
Резонансная теория возмущений
Рис. 2. Сверху: зависимость потенциальной энергии U ψ2 εV0 cos 
 n2 m2 ψ2 в резонансном
n2 m2 ψ2 в резонансном
гамильтониане от угла. Снизу: фазовый портрет математического маятника – фазовый портрет нелинейного резонанса. На обоих рисунках сепаратриса показана красным цветом
Что касается частоты малых колебаний вблизи центра резонанса, она может быть определена на основе уравнений движения. Так из канонических уравнений для гамильтониана (17) следует, что:
|
εKV0 |
n |
2 |
m |
2 |
sin n |
2 |
m |
2 |
ψ2 |
0 |
(20) |
ψ2 |
|
|
|
|
Считая отклонения от центра резонанса малыми, разложим второе слагаемое в ряд Тейлора до членов первого порядка по ψ2, получим уравнение гармонического осциллятора, откуда найдется и искомая частота:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εKV0 n |
2 |
2 |
ψ2 |
0 |
|
~ |
εKV0 n |
2 |
2 |
|
(21) |
|
ψ2 |
|
m |
ω |
|
m |
||||||||
Итоговые замечания:
1.Как следует из (19), ширина резонанса пропорциональна 
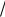 ε , что при малых значениях ε много больше, чем ε1 и, конечно, ε2. Отчасти по этой причине резонанс принципиально не мог быть описан в рамках канонической теории возмущений, где разложение ведется именно по целочисленным степеням малого параметра.
ε , что при малых значениях ε много больше, чем ε1 и, конечно, ε2. Отчасти по этой причине резонанс принципиально не мог быть описан в рамках канонической теории возмущений, где разложение ведется именно по целочисленным степеням малого параметра.
2.Если бы вместо равенства (12) выбрали Vn, m J1 , J2 V n,m J1 , J2 eiα , где α – не-
которая фаза, то получили бы качественно ту же картину резонанса, лишь сдвинутую вдоль горизонтальной оси ψ2.
- 7 -
Малышев А.И.
II.Резонанс в системе с полутора степенями свободы
Впредыдущем разделе обсуждалось построение резонансной теории возмущений на примере консервативной системы с двумя степенями свободы – был описан так называемый внутренний резонанс между степенями свободы или резонанс связи. Рассмотрим теперь резонанс другой природы – резонанс между колебаниями одномерной нелинейной системы и внешним периодическим по времени полем.
Для начала определимся с терминологией, ибо понятие полуцелого числа степеней свободы совсем не тривиально. Вообще, под числом степеней свободы в механике принято понимать количество обобщенных координат, необходимое для однозначного описания положения системы. При этом в случае N степеней свободы задача математически сводится к решению системы из 2N дифференциальных уравнений первого порядка (или N уравнений второго порядка). При решении задач биомеханики, электромеханики и т.п. зачастую возникает ситуация, когда количество дифференциальных уравнений первого порядка, описывающих систему, является нечетным. А поскольку привычной является ситуация, когда число степеней свободы вдвое меньше числа уравнений, то и появилось понятие полуцелого числа степеней свободы. Впоследствии оно расширило границы своей применимости. Скажем, в книге [6] система с N степенями свободы и периодической зависимостью от времени в гамильтониане называется системой с N 1 2 степенями свободы, поскольку «время явля-
2 степенями свободы, поскольку «время явля-
ется дополнительной канонической переменной», похожей на угловую переменную.
Итак, рассмотрим механическую систему с гамильтонианом: |
|
H I,θ,t H0 I εV I,θ,t . |
(22) |
Здесь ε – малый параметр. Переменные действие-угол относятся к невозмущенной системе H0(I), ее частота:
ω I |
dH0 |
. |
(23) |
|
|||
|
dI |
|
|
Как уже указывалось, внешнее поле периодично по времени: V I,θ,t T V I,θ,t . Также как обычно есть и периодичность по переменной θ с периодом 2π. Разложим слагаемое возмущения в двойной ряд Фурье с нулевым средним:
V I,θ,t Vn,m I ei nθ mΩt . |
(24) |
n,m |
|
Здесь Ω 2π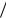 T – характерная частота внешнего поля, а суммирование по обоим индексам идет в бесконечных пределах. Что касается среднего значения возмущения, опущенного в (24), относительно него можно сделать замечание, аналогичное сделанному ранее при записи ряда (8).
T – характерная частота внешнего поля, а суммирование по обоим индексам идет в бесконечных пределах. Что касается среднего значения возмущения, опущенного в (24), относительно него можно сделать замечание, аналогичное сделанному ранее при записи ряда (8).
Рассмотрим далее резонанс ω IR Ω – это равенство является уравнением для определения резонансного значения действия IR.
- 8 -

Резонансная теория возмущений
Как и в предыдущем разделе, заметим здесь, что вблизи резонанса, где I ≈ IR, разность частот ω(I) – Ω стремится к нулю, поэтому разность θ – Ωt является медленной функцией времени по сравнению с θ или Ωt.
Совершим каноническое преобразование посредством производящей функции
F2 θ Ωt J IR |
(25) |
и введем фазу ψ = θ – Ωt, а также сдвинем начало отсчета по действию в область резонанса: J = I – IR. Новый гамильтониан при этом приобретает вид:
~ |
H |
F2 |
H0 J IR ε Vn,m J IR e |
i nψ n m Ωt |
Ω J IR |
. |
(26) |
H |
t |
|
|||||
|
|
n,m |
|
|
|
|
Гамильтониан (26) все еще является точным. Далее сделаем ряд приближений. Так, поскольку речь идет о поведении динамической системы вблизи резонанса, будем рассматривать значения переменной J – малые по сравнению с IR. Разложим слагаемые в гамильтониане в ряд Тейлора вблизи нуля по степеням J, оставляя лишь члены не выше второго порядка. Ввиду малости второго слагаемого, обеспечиваемой множителем ε, значение коэффициентов Vn,m(I) возьмем при резонансном значении действия. В итоге, получим
~ |
H0 IR ω IR Ω J |
K |
|
2 |
ε Vn,m IR e |
i nψ n m Ωt |
ΩIR |
, |
(27) |
H |
|
J |
|
|
|||||
2 |
|
|
|||||||
|
|
|
|
n,m |
|
|
|
|
где введено обозначение K d2H0 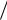 dI2 I IR . Исключим первое и последнее слагаемые как постоянные, а также занулим второе, поскольку ω(IR) = Ω. В результате получим:
dI2 I IR . Исключим первое и последнее слагаемые как постоянные, а также занулим второе, поскольку ω(IR) = Ω. В результате получим:
~ |
|
K |
|
2 |
ε Vn,m IR e |
i nψ n m Ωt |
. |
(28) |
H |
|
J |
|
|
||||
2 |
|
|
||||||
|
|
|
|
n,m |
|
|
|
Далее усредним это выражение по быстрой фазе Ωt – останутся лишь слагаемые с m = –n:
|
|
|
K |
|
|
ε Vn, n IR e |
|
|
|
~ |
|
|
2 |
inψ |
. |
(29) |
|||
H |
|
J |
|
|
|||||
2 |
|
|
|||||||
|
|
|
|
|
n |
|
|
|
|
Оставляя теперь самые медленные слагаемые в сумме по n, будем иметь:
|
|
|
K |
|
|
ε V1, 1 |
IR |
e |
|
|
IR |
e |
|
. |
|
~ |
|
|
2 |
iψ |
V 1,1 |
iψ |
|
||||||||
H |
|
J |
|
|
|
(30) |
|||||||||
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как правило, в реальных системах V1, 1 IR V 1,1 IR , поэтому положим далее
V |
|
I |
|
V |
I |
|
|
V0 |
, |
(31) |
1 |
R |
R |
|
|||||||
1, |
|
1,1 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
(см. также замечание 2 на стр. 7) тогда резонансный гамильтониан примет вид:
Hres |
|
K |
J2 εV0 cosψ |
(32) |
|
||||
|
2 |
|
|
|
- 9 -

Малышев А.И.
Как и при обсуждении внутреннего резонанса, вновь получили гамильтониан математического маятника. Это позволяет легко найти уравнение сепаратрисы резонанса:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εV |
|
K |
J2 εV cosψ |
|
|
J 2 |
εV0 |
|
cos |
ψ |
|
(33) |
||||||
|
|
|
||||||||||||||||
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
K |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и его ширину |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
J 4 |
|
εV0 |
|
|
|
|
|
|
|
(34) |
|||
|
|
|
|
|
K |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из уравнений движения, отвечающих гамильтониану (32), нетрудно рассчитать и частоту малых колебаний вблизи центра резонанса:
J εV0 sinψ |
|
|
|
|
|
|
|
|
|
~ |
|
|
(35) |
||
|
ψ εKV0 sinψ 0 |
ω εKV0 |
|
||||
ψ KJ |
|
|
|
|
|
|
|
Нетрудно заметить, что ввиду универсальности резонансного гамильтониана – гамильтониана математического маятника – выражения (33)-(35) аналогичны (18), (19) и (21), несмотря на то, что речь идет о физически различных механических системах.
- 10 -
