4) Когда внутри магнетика токи намагничивания j′ равны нулю?

Покажем, что токи намагничивания внутри магнетика равны нулю, если: 1) магнетик однородный и 2) внутри него нет токов проводимости, т.е. j =0. В этом случае остаются только поверхностные токи намагничивания.

Для доказательства воспользуемся теоремой о циркуляции вектора J по произвольному контуру Г, взятому целиком внутри магнетика (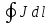 = I^′). В случае однородного магнетика (первое условие) можно заменить J на χH (см. (5.38)) и, т.к. магнитная восприимчивость χ в данном случае постоянная, вынести ее за знак интеграла, тогда получим

I^′ = χ .

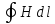Теперь воспользуемся теоремой о циркуляции для вектора H (5.36), согласно которой 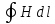=I – алгебраической сумме токов проводимости, охватываемых контуром Г, и для однородного магнетика получим

I^′ = χ I. (5.40)

Это соотношение между токами справедливо для любого контура внутри магнетика, в том числе и для очень малого контура, когда I^′ и I можно заменить на их малые значения, соответственно, dI^′ и dI, а они в свою очередь равны dI^′ = j_n^′dS и dI = j_ndS. Тогда j_n^′dS = j_ndS и после сокращения на dS мы получим j_n^′ = χ j_n . Последнее равенство справедливо для любой ориентации контура, т.е. при любом направлении нормали n к нему. А это значит, что таким же равенством связаны и сами векторы j^′ и j :

j^′ = χ j . (5.41)

Отсюда следует, что для однородного магнетика j^′ = 0 , если j^′ = 0, что и требовалось доказать.

5) Граничные условия для b и h на границе раздела двух однородных магнетиков.

Граничные условия для вектора B получаем, используя теорему Гаусса для него (5.9) 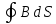= 0. При этом действуем точно так же, как при определении граничных условий для вектора P и D в лекции 4 разделы 4.4 г) и 4.5.3. 2) даже рисунок тот же рис.7. Тогда получим, что поток вектора B через замкнутую поверхность S в виде прямого цилиндра охватывающего элемент поверхности границы раздела ∆S , при стремлении к нулю его высоты будет равен потоку через торцы цилиндра, а именно B_2n∆S – B_1n∆S, который, согласно теореме, равен нулю. Тогда после сокращения на ∆S, получим

B_2n = B_1n , (5.42)

т.е. нормальная составляющая вектора B одинаковая по обе стороны границы раздела двух магнетиков. Эта величина скачка не испытывает.

Граничные условия для вектора H получаем, используя теорему о циркуляции 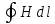=I (5.36) так же, как для вектора E. Для большей общности положим, что по поверхности раздела магнетиков 1 и 2 течет поверхностный ток проводимости с линейной плотностью i. Применим теорему о циркуляции вектора H к очень малому контуру, в виде прямоугольника, который охватывает границу раздела длиной ℓ (это и длина прямоугольника), а его плоскость перпендикулярна поверхности раздела (при этом нормаль N к контуру параллельна поверхности раздела). Для ясности смотри рис.21. Тогда устремив полувысоту h контура к нулю и, соответственно, пренебрегая вкладом в циркуляцию по боковым сторонам (4h) контура, получим для всего контура:

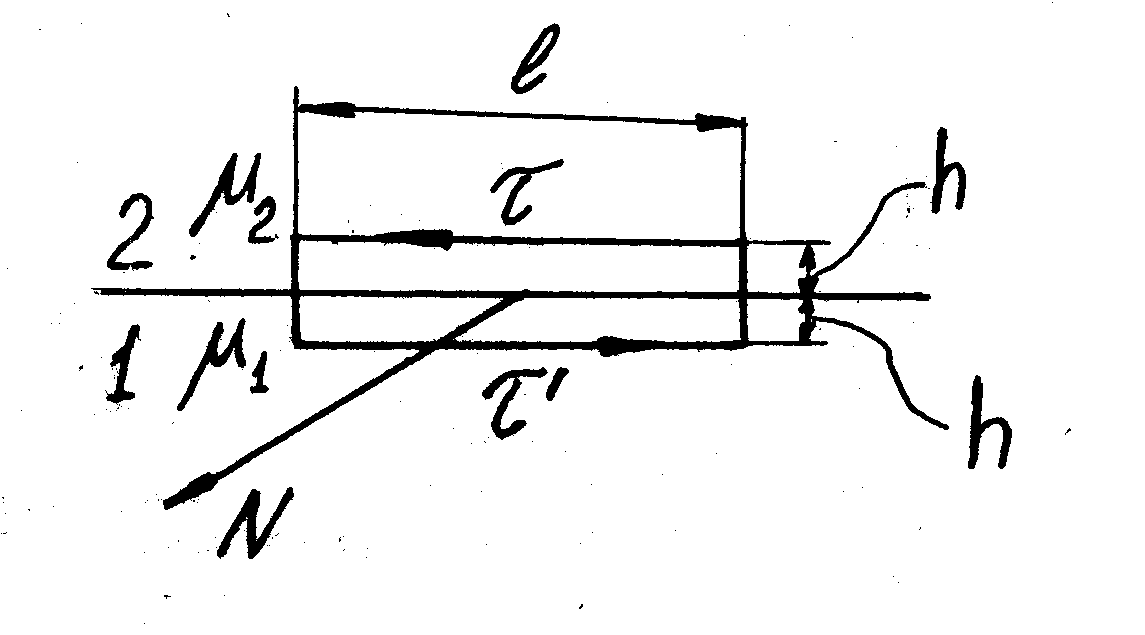
H_2τℓ + H_1τ′ℓ = i_Nℓ , Рис.21.

где i_N – проекция вектора i на нормаль N к контуру (вектор N образует с направлением обхода по контуру правовинтовую систему). Взяв обе проекции вектора H на общий орт касательной τ (в среде 2) (другими словами приведя все к общей касательной τ), получим H_2τ = – H_1τ′ и после сокращения на предыдущее уравнение примет вид

H_2τ – H_1τ = i_N , (5.43)

т.е. тангенциальная составляющая вектора H при переходе границы раздела двух магнетиков претерпевает скачек, связанный с наличием поверхностного тока проводимости.

Если на границе раздела магнетиков токов проводимости нет (i = 0), то тангенциальная составляющая вектора H оказывается одинаковой по обе стороны границы раздела:

H_2τ = H_1τ . (5.44)

Итак, если на границе раздела двух однородных магнетиков тока проводимости нет, то при переходе этой границы составляющие B_n и H_τ изменяются непрерывно, без скачка, а составляющие B_τ и H_n при этом претерпевают скачек.