
- •III. Ряды
- •1.2. Ряды с неотрицательными членами
- •Найти все значения , при которых сходится ряд :
- •Исследовать на сходимость ряд с помощью признака Даламбера:
- •Исследовать на сходимость ряд с помощью признака Коши:
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§ 2. Функциональные ряды
- •2.1. Признаки сходимости функциональных рядов
- •Свойства функциональных рядов
- •2.2. Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение основных элементарных функций в ряд Маклорена
- •§ 3. Тригонометрические ряды Фурье
§ 3. Тригонометрические ряды Фурье
Если функция
![]() кусочно-непрерывна и имеет кусочно-непрерывную
производную
кусочно-непрерывна и имеет кусочно-непрерывную
производную![]() в интервале
в интервале![]() ,
причем все точки разрыва
,
причем все точки разрыва![]() регулярны (т. е.
регулярны (т. е.![]() ),
то функция
),
то функция![]() на этом интервале может быть представленарядом Фурье
на этом интервале может быть представленарядом Фурье
 ,
,
где
 ;
; .
.
В частности:
а) если функция
![]() четная, то имеем
четная, то имеем
 ,
,
где

![]() ;
;
б) если функция
![]() нечетная, то получаем
нечетная, то получаем
 ,
,
где

![]() .
.
Функцию
![]() ,
определенную в интервале
,
определенную в интервале![]() и обладающую в нем приведенными выше
свойствами четности, можно в этом
интервале разложить в ряд Фурье только
по синусам или только по косинусам.
и обладающую в нем приведенными выше
свойствами четности, можно в этом
интервале разложить в ряд Фурье только
по синусам или только по косинусам.
Дифференцирование
рядов Фурье. Если
функция
![]() непрерывна, а её производная
кусочно-непрерывна на отрезке
непрерывна, а её производная
кусочно-непрерывна на отрезке![]() и
и![]() ,
то ряд Фурье для
,
то ряд Фурье для![]() получается из ряда Фурье для
получается из ряда Фурье для![]() почленным дифференцированием.
почленным дифференцированием.
Интегрирование
рядов Фурье. Ряд
Фурье, даже расходящийся, интегрируемой
по Риману в интервале
![]() функции
функции![]() можно интегрировать почленно в этом
интервале.
можно интегрировать почленно в этом
интервале.
Разложение в ряд
Фурье функций, зависящих от
![]() и
и![]() ,
удается иногда получить с помощью формул
Эйлера:
,
удается иногда получить с помощью формул
Эйлера:
![]() ;
;  ;
;![]() .
.
Для этого следует
подставить в формулу, задающую
рассматриваемую функцию, выражения для
косинуса и синуса и получившуюся функцию
от
![]() разложить в ряд по степеням
разложить в ряд по степеням![]() ,
а затем вернуться к переменной
,
а затем вернуться к переменной![]() с помощью формулы
с помощью формулы
![]() .
.
В результате получится искомое разложение заданной функции в ряд Фурье.
Пример 3.1. Разложить в ряд Фурье функцию
![]() .
.
Решение.
Воспользуемся формулами Эйлера. Подставим
выражения для синуса и косинуса в функцию
и представим получившуюся рациональную
функцию параметра
![]() в виде суммы двух дробей следующим
образом:
в виде суммы двух дробей следующим
образом:
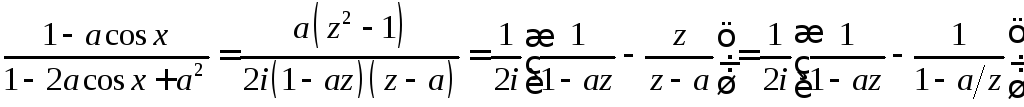 .
.
Поскольку
![]() ,
,![]() ,
то дроби
,
то дроби![]() и
и![]() можно разложить в степенные ряды. (Эти
дроби представляют собой суммы бесконечно
убывающих геометрических прогрессий.)
В результате получим ряд Фурье функции
можно разложить в степенные ряды. (Эти
дроби представляют собой суммы бесконечно
убывающих геометрических прогрессий.)
В результате получим ряд Фурье функции![]() в комплексной форме:
в комплексной форме:
 .
.
Заметив, что
 ,
получим
,
получим .
.
Пример 3.2.
Разложить
в ряд Фурье неограниченную периодическую
функцию
![]() .
.
Решение.
Применим для разложения метод, основанный
на применении формул Эйлера. Положив
![]() ,
,![]() (следовательно,
(следовательно,![]() ),
будем иметь
),
будем иметь
 .
.
Заметив, что
![]() ,
,![]() и
и![]() ,
получим, разложив в степенной ряд
логарифм
,
получим, разложив в степенной ряд
логарифм![]() ,
,
 .
.
В результате будем иметь
 .
.
Поскольку в левой части этого равенства стоит действительное число, мнимая часть его правой части равна нулю:
 .
.
Следовательно,
 ,
,
![]() .
.
Попутно получилось
разложение в ряд Фурье функции
![]() :
:
 .
.
Пример 3.3.
Найти сумму
ряда
 .
.
Решение.
Ряд
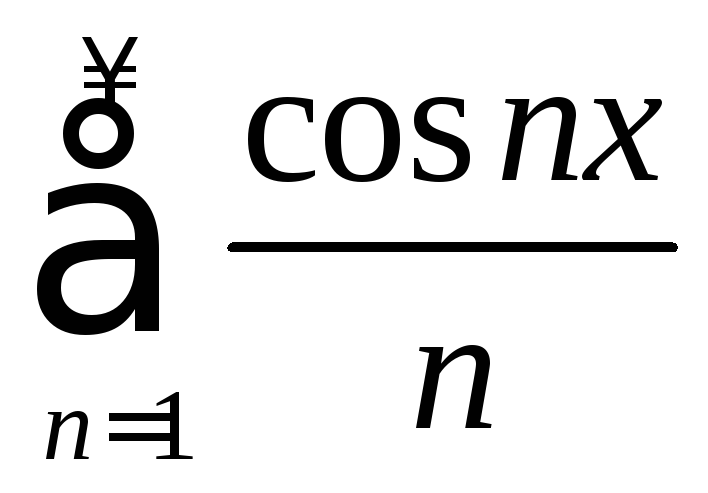 сходится при
сходится при![]() .
Рассмотрим ряд
.
Рассмотрим ряд ,
сходящийся при любом
,
сходящийся при любом![]() .
Обозначим
.
Обозначим и
и .
Тогда
.
Тогда
 ,
,
![]() .
.
Преобразуем выражение, стоящее под знаком логарифма:


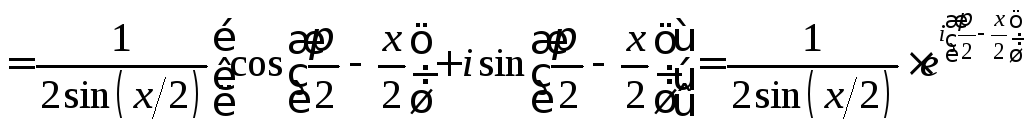 .
.
Таким образом,
 .
.
Откуда сразу находится сумма ряда:
 ,
, ![]() .
.
Заодно мы доказали, что
 ,
, ![]() .
.
Разложить в ряд
Фурье функцию
![]() ,
указать промежутки, в которых сумма
ряда Фурье равна функции
,
указать промежутки, в которых сумма
ряда Фурье равна функции![]() ,
и найти сумму ряда в указанной точке
,
и найти сумму ряда в указанной точке![]() :
:
|
3.1.
|
|
|
3.2.
|
|
|
3.3.
|
|
|
3.4.
|
|
Разложить в ряд Фурье функцию
 ,
и, пользуясь полученным разложением,
найти сумму ряда Лейбница
,
и, пользуясь полученным разложением,
найти сумму ряда Лейбница .
.
Разложить в ряд
Фурье функцию
![]() на указанном промежутке, считая длину
промежутка периодом:
на указанном промежутке, считая длину
промежутка периодом:
|
3.6.
|
|
|
3.7.
|
|
|
3.8.
|
|
|
3.9.
|
|
3.10.
![]() ,
,![]() на отрезке
на отрезке![]() .
Доказать с помощью получившегося
разложения, что
.
Доказать с помощью получившегося
разложения, что .
.
3.11. Разложить в ряд Фурье функцию

периодически продолженную на всю числовую ось с периодом 3. Нарисовать график суммы ряда.
Разложить в ряд Фурье периодическую функцию:
|
3.12.
|
3.13.
|
|
3.14.
|
3.15.
|
|
3.16.
|
|
3.17. Разложить
в ряд Фурье на интервале
![]() по синусам функцию:
по синусам функцию:
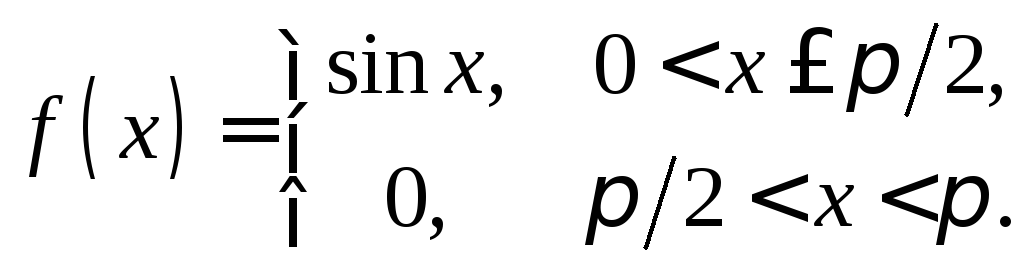
3.18. Разложить
функцию
![]() в ряд Фурье:
в ряд Фурье:
а) на отрезке
![]() по косинусам;
по косинусам;
б) на интервале
![]() по синусам;
по синусам;
в) на интервале
![]() по синусам и косинусам.
по синусам и косинусам.
Пользуясь этими разложениями, найти суммы рядов:
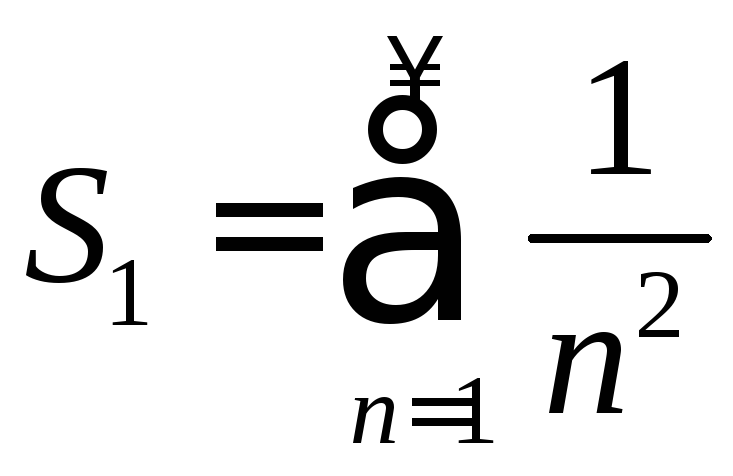 ,
,  ,
, .
.
3.19. Разложить в ряд Фурье по синусам функцию

Пользуясь формулами Эйлера, разложить в ряд Фурье функцию:
|
3.20.
|
|
|
3.21.
|
|
|
3.22.
|
|
3.23. Исходя из разложения
 ,
,
почленным
интегрированием получить разложение
в ряд Фурье на интервале
![]() функций
функций![]() и
и![]() .
.
Разложить в ряд Фурье неограниченные периодические функции:
|
3.24.
|
3.25.
|
|
3.26.
|
|
Найти сумму ряда:
|
3.27.
|
3.28.
|
|
3.29.
|
3.30.
|
Ответы: 3.1.

![]() ;
0.3.2.
;
0.3.2.
![]()
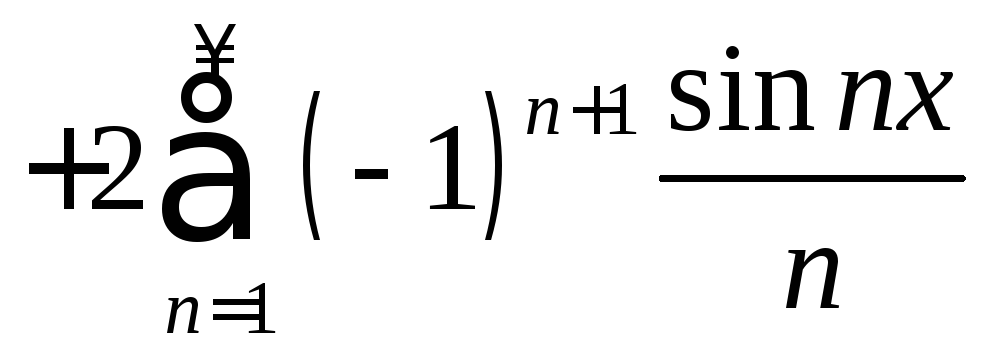 ,
,![]() ;
;![]() .3.3.
.3.3.  ,
,![]() ;
;![]() .3.4.
.3.4.
 ,
,![]() ;
;![]() .3.5.
.3.5.
 ;
; .3.6.
.3.6.
 .3.7.
.3.7.
 .3.8.
.3.8.
 .3.9.
.3.9. ![]()
 .3.10.
.3.10.  .3.11.
.3.11. ![]()
 .
.
3.12.
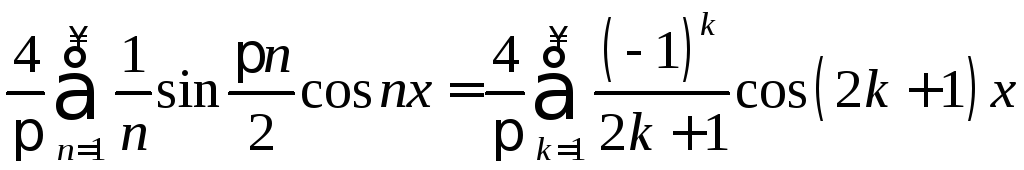 .3.13.
.3.13.
 .3.14.
.3.14.
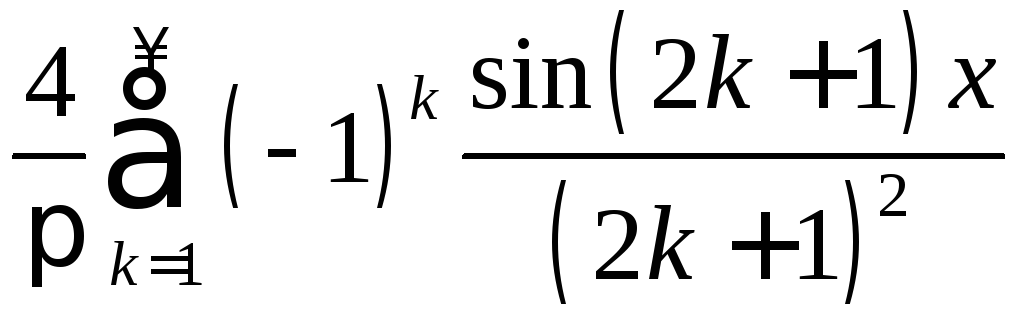 .3.15.
.3.15.
 .3.16.
.3.16.  .3.17.
.3.17.  .3.18.
.3.18.  .
.
3.19.  .3.20.
.3.20.  ,
,![]() .
.
3.21.  .3.22.
.3.22.  .3.23.
.3.23.  ;
; .3.24.
.3.24.  ,
,![]() ,
,![]() .3.25.
.3.25. 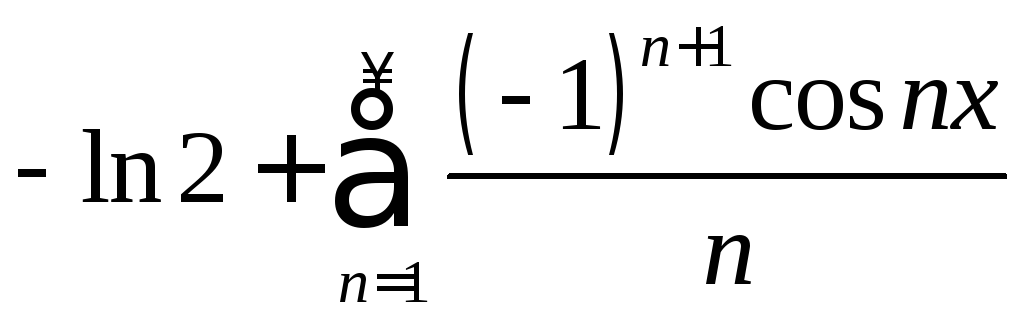 .3.26.
.3.26.  ,
,
![]() ,
,
![]() .3.27.
.3.27. ![]() .3.28.
.3.28. ![]() .
.
3.29.  .3.30.
.3.30.  .
.

 .
. на интервале
на интервале на отрезке
на отрезке .
. .
. .
. .
. .
. .
. .
.