
- •III. Ряды
- •1.2. Ряды с неотрицательными членами
- •Найти все значения , при которых сходится ряд :
- •Исследовать на сходимость ряд с помощью признака Даламбера:
- •Исследовать на сходимость ряд с помощью признака Коши:
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§ 2. Функциональные ряды
- •2.1. Признаки сходимости функциональных рядов
- •Свойства функциональных рядов
- •2.2. Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение основных элементарных функций в ряд Маклорена
- •§ 3. Тригонометрические ряды Фурье
Ряды Тейлора и Маклорена
Если функция
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() и имеет в этой точке производные всех
порядков, то степенной ряд
и имеет в этой точке производные всех
порядков, то степенной ряд называетсярядом
Тейлора функции
называетсярядом
Тейлора функции
![]() в точке
в точке
![]() .
.
В случае, когда
![]() ,
ряд Тейлора называютрядом
Маклорена.
,
ряд Тейлора называютрядом
Маклорена.
Остаточный член
ряда Тейлора
 может быть представлен:
может быть представлен:
а) в форме Лагранжа
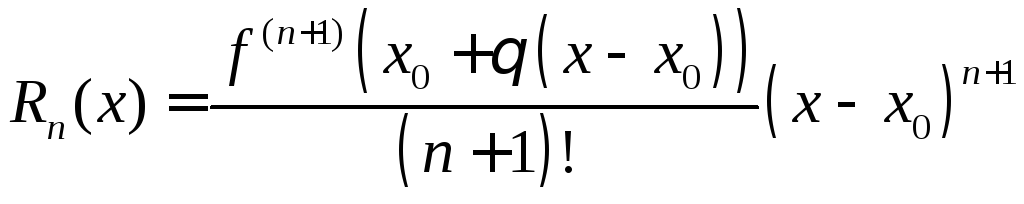 ,
,
![]() ;
;
б) в форме Коши
 ,
,
![]() ;
;
в) в интегральной форме
 .
.
Необходимое и
достаточное условие сходимости ряда
Тейлора.
Для того, чтобы ряд Тейлора функции
![]() сходился к самой функции
сходился к самой функции![]() ,
остаточный член ряда
,
остаточный член ряда![]() должен стремиться к 0 при
должен стремиться к 0 при![]() .
.
Если для отрезка
![]() при любом
при любом![]()
![]() ,
то для всех
,
то для всех![]()
![]() .
.
Разложение основных элементарных функций в ряд Маклорена
1.
 .
.
2.
 ,
,![]() .
.
3.
 .
.
4.
 .
.
5.
 ,
где
,
где ,
,![]() .
.
В последнем
разложении
![]() ,
иначе разложение будет содержать лишь
,
иначе разложение будет содержать лишь![]() слагаемое.
слагаемое.
Важные частные случаи формулы (5):
 ,
, ![]() .
.
 ,
, ![]() .
.
Приемы и методы разложения функций в ряд Тейлора. Обычно коэффициенты ряда Тейлора находят с помощью формул (1) – (5), применяя различные приемы: представление данной функции в виде суммы более простых функций, замену переменной, почленное дифференцирование и интегрирование ряда и др.
Решение дифференциальных уравнений с помощью степенных рядов. Рассмотрим задачу Коши
![]() ,
,
![]() ,
, ![]() .
.
Если функции
![]() ,
,![]() ,
,![]() представляются степенными рядами вида
представляются степенными рядами вида ,
сходящимися к этим функциям в некоторой
окрестности точки
,
сходящимися к этим функциям в некоторой
окрестности точки![]() ,
то существует единственное решение
задачи Коши, представимое в виде
степенного ряда
,
то существует единственное решение
задачи Коши, представимое в виде
степенного ряда ,
сходящегося в некоторой окрестности
точки
,
сходящегося в некоторой окрестности
точки![]() .
.
Найдя из равенства
 с помощью дифференцирования степенные
ряды для
с помощью дифференцирования степенные
ряды для![]() и
и![]() ,
подставив в дифференциальное уравнение
вместо
,
подставив в дифференциальное уравнение
вместо![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() их разложения в степенные ряды и произведя
арифметические действия над рядами,
получим равенство степенных рядов. Из
полученного равенства можно последовательно
найти коэффициенты
их разложения в степенные ряды и произведя
арифметические действия над рядами,
получим равенство степенных рядов. Из
полученного равенства можно последовательно
найти коэффициенты![]() и тем самым решить задачу Коши.
и тем самым решить задачу Коши.
Нахождение сумм рядов. При вычислении сумм числовых рядов иногда удается представить ряд в виде линейной комбинации известных рядов:
|
|
|
|
|
|
|
|
|
|
Пример 2.5.
Найти сумму
ряда
 .
.
Решение.
Дифференцируя почленно ряд
 ,
получаем
,
получаем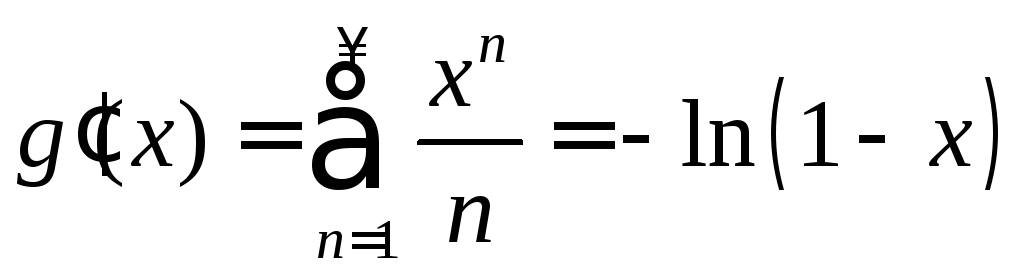 .
Следовательно,
.
Следовательно,

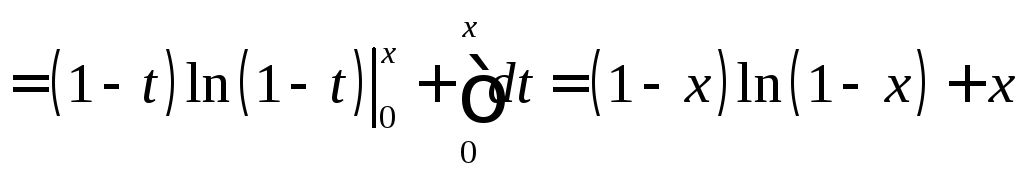 .
.
Пример 2.6.
Разложить
функцию
![]() в
ряд по степеням
в
ряд по степеням![]() .
.
Решение.


 =
=

 .
.
Из последней
формулы видно, что для первого ряда
![]() ,
а для второго ряда
,
а для второго ряда![]() .
Значит, радиус сходимости для суммы
рядов равен
.
Значит, радиус сходимости для суммы
рядов равен![]() .
Окончательно получим
.
Окончательно получим
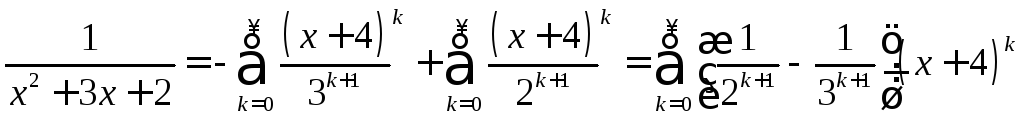 .
.
Пример 2.7.
Найти сумму
ряда
 .
.
Решение.
Дифференцируя почленно ряд
 ,
получаем
,
получаем .
Следовательно,
.
Следовательно,

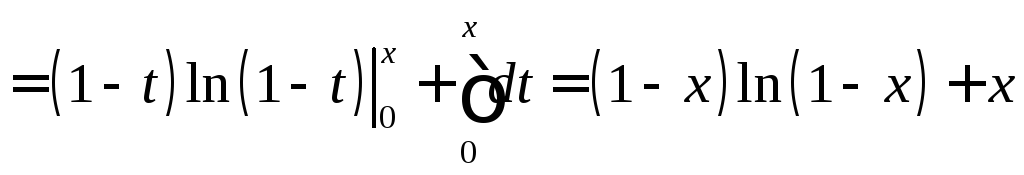 .
.
Пример 2.8.
Найти сумму ряда
 ,
а затем вычислить сумму ряда
,
а затем вычислить сумму ряда .
.
Решение. Ряд
 сходится на интервале
сходится на интервале![]() (геометрическая прогрессия). Его сумма
равна
(геометрическая прогрессия). Его сумма
равна![]() .
На любом отрезке
.
На любом отрезке![]() ,
где
,
где![]() ,
ряд сходится равномерно, а его члены –
непрерывные функции. Интегрируем
почленно этот ряд на отрезке
,
ряд сходится равномерно, а его члены –
непрерывные функции. Интегрируем
почленно этот ряд на отрезке![]() ,
где
,
где![]() :
:
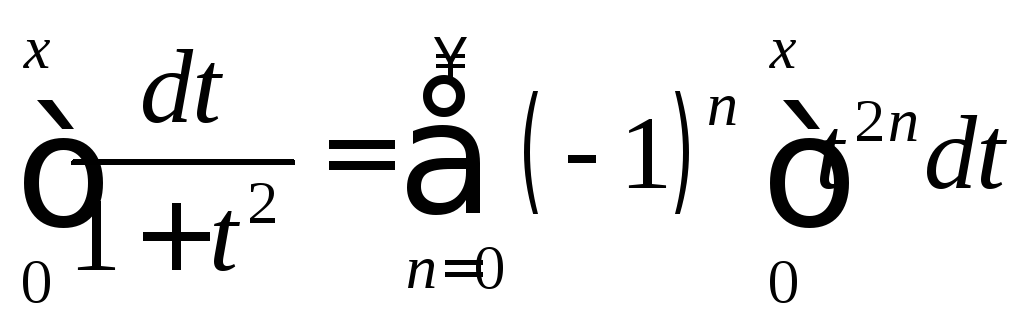 ;
;  .
.
Положим
 ,
тогда
,
тогда ;
следовательно,
;
следовательно, .
.
Пример 2.9.
Найти сумму
ряда
 .
.
Решение. Рассмотрим степенной ряд

 .
.
Ряд сходится
равномерно для
![]() .
Возьмем
.
Возьмем![]() .
Тогда
.
Тогда
 .
.
Разложить функцию в ряд Маклорена и найти радиус сходимости полученного ряда:
|
2.49.
|
2.50.
|
|
2.51.
|
2.52.
|
|
2.53.
|
2.54.
|
|
2.55.
|
2.56.
|
|
2.57.
|
2.58.
|
|
2.59.
|
2.60.
|
|
2.61.
|
2.62.
|
Разложить функцию
в ряд Тейлора в окрестности точки
![]() и найти радиус сходимости полученного
ряда:
и найти радиус сходимости полученного
ряда:
|
2.63.
|
2.64.
| |
|
2.65.
|
| |
|
2.66.
|
| |
|
2.67.
|
2.68.
| |
Перемножив соответствующие ряды, разложить функцию в ряд Маклорена и найти радиус сходимости полученного ряда:
|
2.69.
|
2.70.
|
С помощью
дифференцирования ряда
 доказать, что:
доказать, что:
|
2.71.
|
|
|
2.72.
|
|
Применив почленное дифференцирование, вычислить сумму ряда:
|
2.73.
|
2.74.
|
Применив почленное интегрирование, вычислить сумму ряда:
|
2.75.
|
2.76.
|
Вычислить сумму ряда:
|
2.77.
|
2.78.
|
|
2.79.
|
2.80.
|
С помощью разложения подынтегральной функции в ряд с точностью до 0,001 вычислить интеграл:
|
2.81.
|
2.82.
|
|
2.83.
|
2.84.
|
Найти разложение в ряд Маклорена решения дифференциального уравнения, удовлетворяющего заданным начальным условиям:
|
2.85.
|
|
|
2.86.
|
|
|
2.87.
|
|
|
2.88.
|
|
Ответы: 2.49.
 ,
,![]() .2.50.
.2.50.
 ,
,![]() .2.51.
.2.51.  ,
,![]() .2.52.
.2.52.
 ,
,![]() .
.
2.53.  ,
,![]() .2.54.
.2.54.
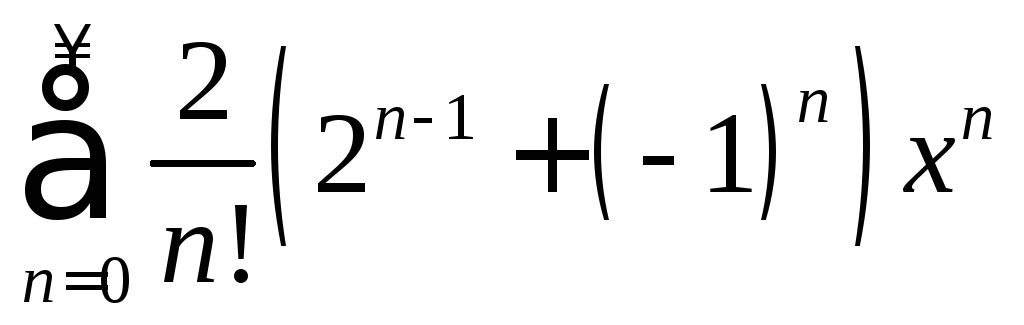 ,
,![]() .
.
2.55.
 ,
,![]() .2.56.
.2.56.
 ,
,![]() .
.
2.57.
 ,
,![]() .2.58.
.2.58.  ,
,![]() .2.59.
.2.59.
 ,
,![]() .2.60.
.2.60.
 ,
,![]() .2.61.
.2.61.
 ,
,![]() .2.62.
.2.62.  ,
,![]() .2.63.
.2.63.
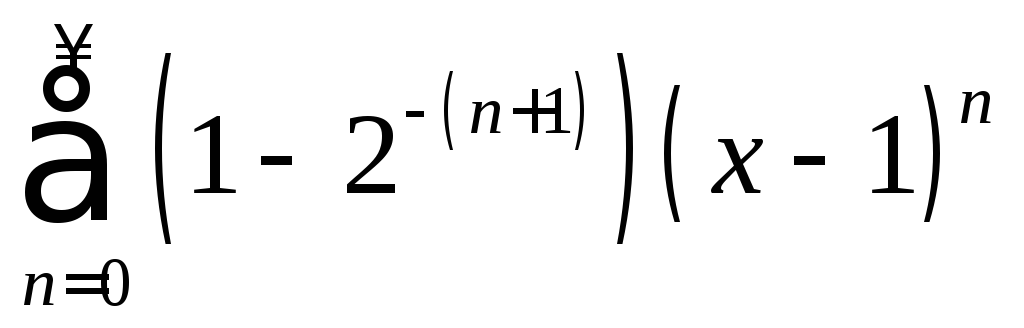 ,
,![]() .
.
2.64.
 ,
,![]() .2.65.
.2.65.

 ,
,![]() .2.66.
.2.66.
 ,
,![]() .2.67.
.2.67.  ,
,![]() .2.68.
.2.68.

 ,
,![]() .2.69.
.2.69.
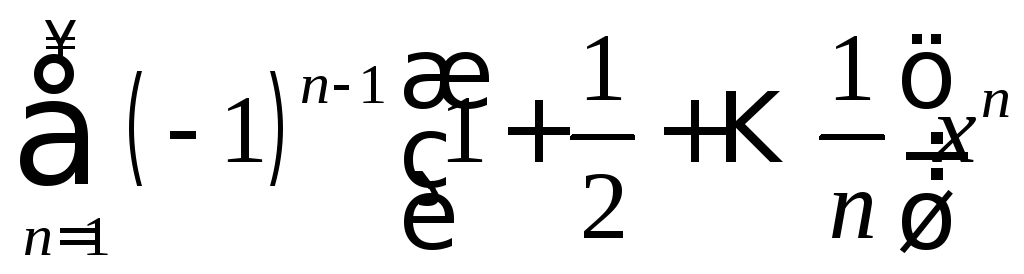 ,
,![]() .2.70.
.2.70.
 ,
,![]() .2.73.
.2.73.
![]() ,
,![]() .
.
2.74.
![]() ,
,![]() .2.75.
.2.75.
![]() .2.76.
.2.76.
![]() ,
,![]() .
.
2.77.
![]() ,
,![]() .2.78.
.2.78. ![]() ,
,![]() .2.79.
.2.79.
![]() ,
,![]() .2.80.
.2.80.
![]() ,
,![]() .2.81.
.2.81.
![]() .2.82.
.2.82.
![]() .2.83.
.2.83.
![]() .2.84.
.2.84.
![]() .2.85.
.2.85.  .2.86.
.2.86.
 .2.87.
.2.87.  .
.
2.88.
 .
.

 .
.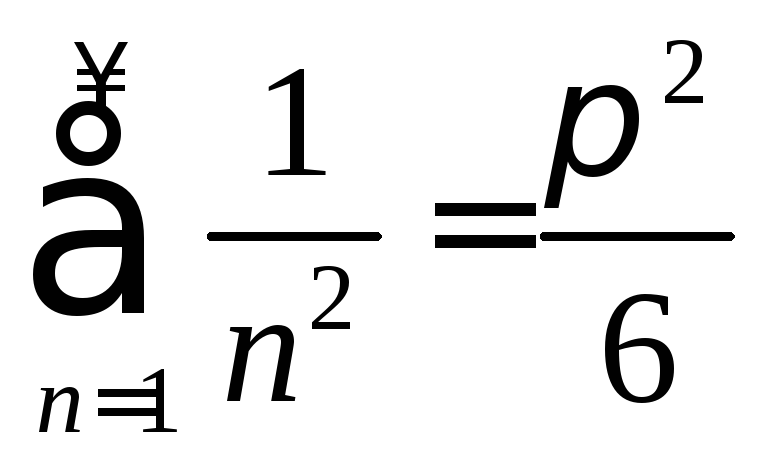 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.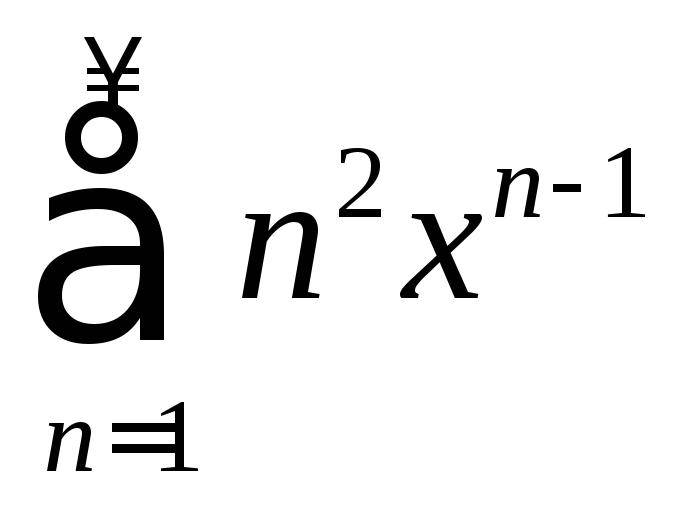 .
. .
. .
.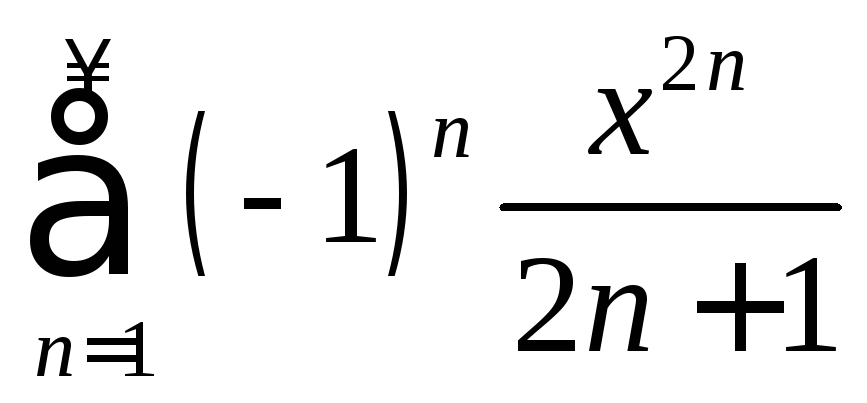 .
. .
.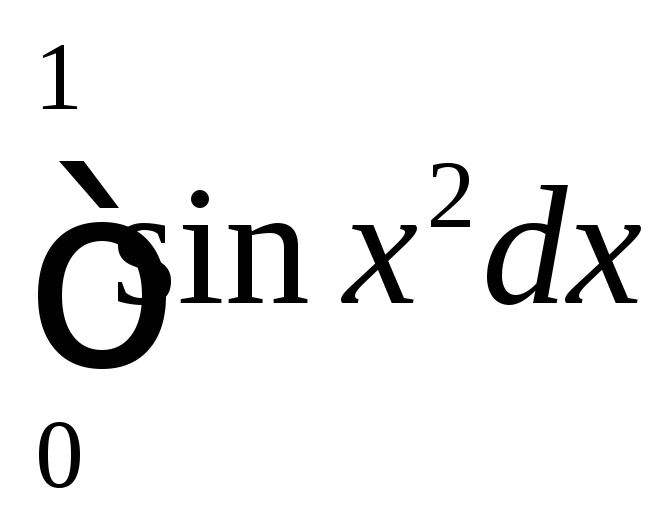 .
. .
. .
.