2.2. Степенные ряды

Функциональный ряд вида , или, называетсястепенным рядом.

Теорема Абеля. Если степенной ряд сходится в точке, то он сходится абсолютно для любого значениятакого, что, а если этот ряд расходится в точке, то он расходится при всяком, для которого.

Для всякого степенного ряда существует неотрицательное числотакое, что ряд абсолютно сходится на интервале.

Число называетсярадиусом сходимости ряда, а интервал –интервалом сходимости ряда.

Для радиуса сходимости степенного рядасправедливы формулы:

; .

Пользоваться этими формулами следует осторожно, т. к. пределы, стоящие в правых частях формул, могут не существовать. Это, например, имеет место, если ряд содержит члены только с четными или нечетными степенями . В таких случаях при определении интервала сходимости следует применять признаки Даламбера или Коши непосредственно.

Степенной ряд 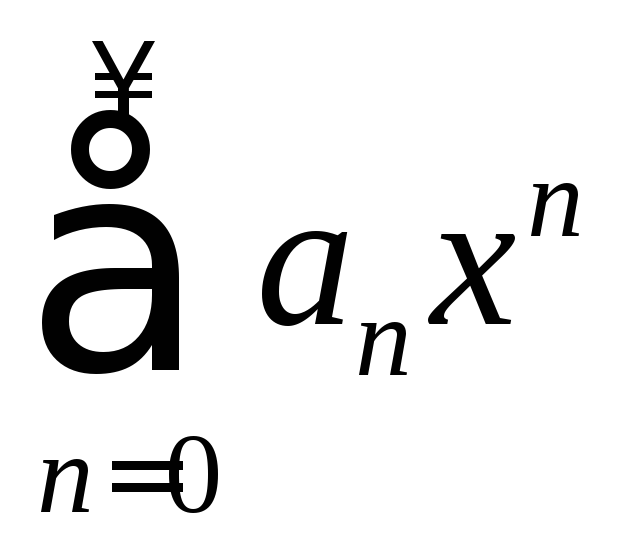представляет собой функцию, непрерывную на интервале, гдерадиус сходимости ряда.

Пусть . Тогда рядсходится на множествеабсолютно и равномерно.

Дифференцирование и интегрирование степенного ряда. Если степенной ряд имеет радиус сходимости, то:

1. в интервале сходимости функцияимеет производные любого порядка, получаемые почленным дифференцированием ряда;

2. внутри интервала сходимости этот ряд можно почленно интегрировать, т. е.

;

3. степенные ряды, получаемые из ряда при почленном дифференцировании и интегрировании, имеют тот же радиус сходимости, что и исходный ряд.

Пример 2.4. Найти область сходимости и абсолютной сходимости ряда:

а) ; б);

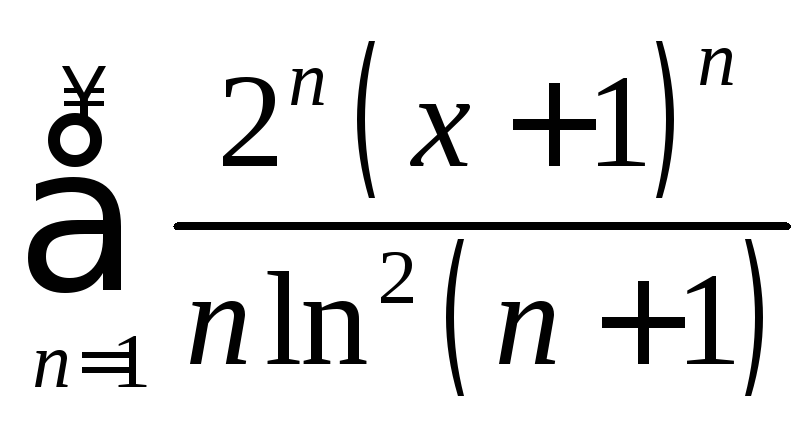в) ; г) .

Решение. а) . Ряд абсолютно сходится на всей числовой прямой.

б) . Ряд сходится абсолютно, если, т. е. в интервале. Приполучаем числовой ряд , который расходится, т. к. для его общего члена справедлива асимптотическая формула. В точкеполучаем знакочередующийся ряд , сходящийся по признаку Лейбница. Следовательно, область сходимости ряда – полуинтервал , а область абсолютной сходимости – интервал.

в) 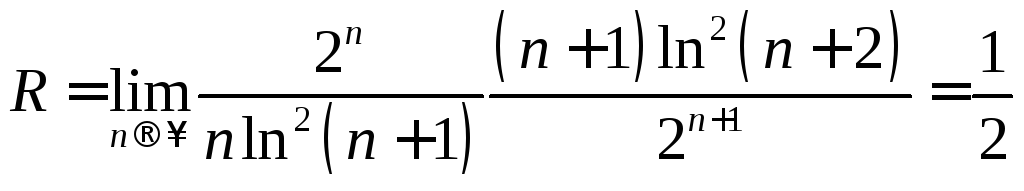.Ряд сходится абсолютно, если , т. е. в интервале. Прииряд абсолютно сходится, т. к. по интегральному признаку сходится ряд

.

Поэтому область абсолютной сходимости ряда – отрезок .

г) Обозначим . Вычислим

.

Очевидно, предел существует, если , т. е.. Приряд расходится (не выполняется необходимое условие сходимости). Следовательно, область сходимости и абсолютной сходимости ряда – интервал.

Найти интервал сходимости степенного ряда:

2.27. .	2.28. .
2.29. .	2.30. .
2.31. .	2.32. .

Найти радиус сходимости и интервал сходимости степенного ряда, исследовать ряд на сходимость и абсолютную сходимость в концах интервала сходимости:

2.33. .	2.34. .
2.35. .	2.36. .
2.37. .	2.38. .
2.39. .	2.40. .
2.41. .	2.42. .

Найти область сходимости ряда:

2.43. .	2.44. .
2.45. .	2.46. .
2.47. .	2.48. .

Ответы: 2.27. .2.28. .2.29. .2.30. .2.31. .2.32. .2.33. ,, приирасходится.2.34. ,, присходится условно, прирасходится.2.35. ,, приирасходится.2.36. ,, приирасходится.2.37. ,, приирасходится.2.38. ,, присходится условно, прирасходится.2.39. ,, прирасходится.2.40. ,, присходится абсолютно, если, и условно, если, присходится абсолютно, если, и расходится, если.2.41. ,, присходится абсолютно, если, и условно, если, присходится абсолютно, если, и расходится, если.2.42. ,, прирасходится.2.43. .2.44. .2.45. .2.46. .2.47. ,.2.48. ,.