
- •III. Ряды
- •1.2. Ряды с неотрицательными членами
- •Найти все значения , при которых сходится ряд :
- •Исследовать на сходимость ряд с помощью признака Даламбера:
- •Исследовать на сходимость ряд с помощью признака Коши:
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§ 2. Функциональные ряды
- •2.1. Признаки сходимости функциональных рядов
- •Свойства функциональных рядов
- •2.2. Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение основных элементарных функций в ряд Маклорена
- •§ 3. Тригонометрические ряды Фурье
§ 2. Функциональные ряды
2.1. Признаки сходимости функциональных рядов
Пусть задана
последовательность функций
![]() ,
определенных на множестве
,
определенных на множестве![]() .
.
Функциональный
ряд
 называетсясходящимся
в точке
называетсясходящимся
в точке
![]() ,если
сходится числовой ряд
,если
сходится числовой ряд
 .
Если сходится ряд
.
Если сходится ряд ,
то ряд
,
то ряд называетсяабсолютно
сходящимся
в точке
называетсяабсолютно
сходящимся
в точке
![]() .
.
Если функциональный
ряд сходится в каждой точке
![]() ,
то этот ряд называютсходящимся
на множестве
,
то этот ряд называютсходящимся
на множестве
![]() .
.
Множества значений
![]() ,
для которых сходятся ряды
,
для которых сходятся ряды
 и
и ,
называются соответственнообластью
сходимости
и областью
абсолютной сходимости ряда
,
называются соответственнообластью
сходимости
и областью
абсолютной сходимости ряда
 .
.
Функция
 называется
называется![]() -й
частичной суммой ряда
-й
частичной суммой ряда
 ,
а предел последовательности частичных
сумм сходящегося на множестве
,
а предел последовательности частичных
сумм сходящегося на множестве![]() ряда называют егосуммой:
ряда называют егосуммой:
![]() .
.
В простейших
случаях для определения области
сходимости ряда
 достаточно применить к этому ряду
известные признаки сходимости числовых
рядов, считая
достаточно применить к этому ряду
известные признаки сходимости числовых
рядов, считая![]() фиксированным.
фиксированным.
Последовательность
функций
![]() называетсяравномерно
сходящейся на множестве
называетсяравномерно
сходящейся на множестве
![]() ,
если:
,
если:
существует предельная функция
 ;
;для любого числа
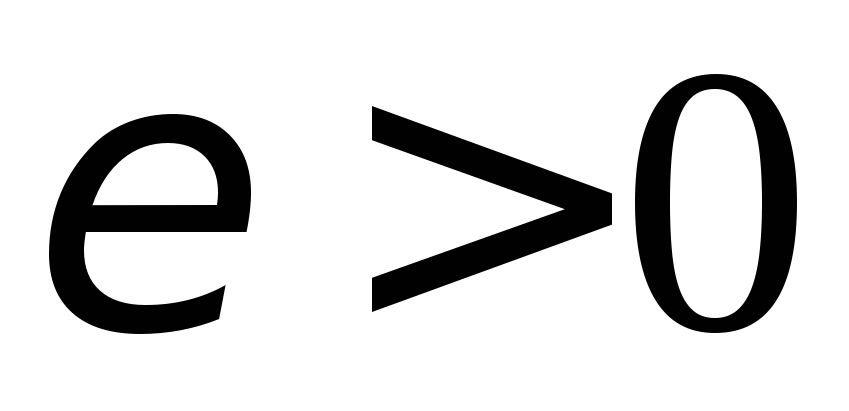 можно указать число
можно указать число такое, что
такое, что для всех
для всех и для всех
и для всех
 .
.
Функциональный
ряд
 называетсяравномерно
сходящимся на множестве
называетсяравномерно
сходящимся на множестве
![]() ,
если на этом множестве равномерно
сходится последовательность его
частичных сумм
,
если на этом множестве равномерно
сходится последовательность его
частичных сумм
![]() или остаток ряда
или остаток ряда![]()
 равномерно сходится к нулю.
равномерно сходится к нулю.
Критерий Коши.
Ряд
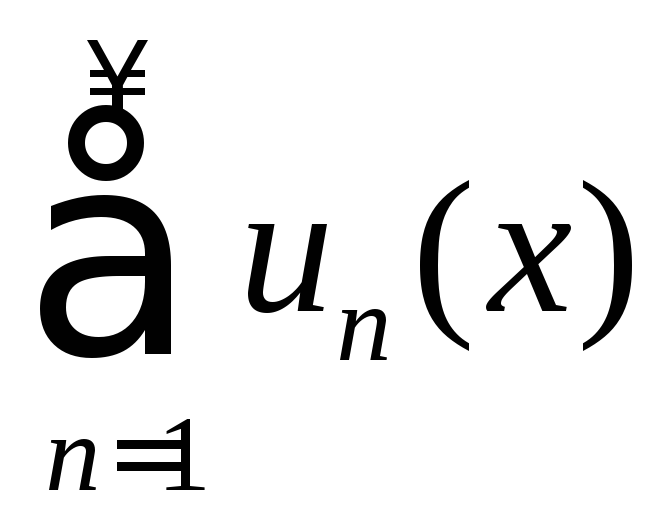 равномерно сходится на множестве
равномерно сходится на множестве![]() тогда и только тогда, когда
тогда и только тогда, когда![]()
![]() .
.
Признак
Вейерштрасса.
Пусть для всех![]() выполняется неравенство
выполняется неравенство![]() .
Пусть, кроме того, числовой ряд
.
Пусть, кроме того, числовой ряд![]() сходится. Тогда ряд
сходится. Тогда ряд сходится на множестве
сходится на множестве![]() абсолютно и равномерно.
абсолютно и равномерно.
В случае, когда
выполняется неравенство
![]() ,
,![]() ,
говорят, что ряд
,
говорят, что ряд мажорируется
рядом
мажорируется
рядом
![]() .
.
Признак Абеля.
Ряд
 сходится равномерно на множестве
сходится равномерно на множестве![]() ,
если:
,
если:
1) ряд
 равномерно сходится на множестве
равномерно сходится на множестве![]() ;
;
2) функции
![]() ограничены в совокупности и при каждом
ограничены в совокупности и при каждом![]() образуют монотонную последовательность.
образуют монотонную последовательность.
Признак Дирихле.
Ряд
 сходится равномерно на множестве
сходится равномерно на множестве![]() ,
если:
,
если:
1) частичные суммы
 в совокупности ограничены;
в совокупности ограничены;
2) последовательность
функций
![]() монотонна для каждого
монотонна для каждого![]() и равномерно на
и равномерно на![]() стремится к нулю при
стремится к нулю при![]() .
.
Свойства функциональных рядов
1. Сумма равномерно сходящегося ряда непрерывных функций есть функция непрерывная.
2. Если члены ряда
 непрерывны и этот ряд равномерно сходится
к своей сумме
непрерывны и этот ряд равномерно сходится
к своей сумме![]() на отрезке
на отрезке![]() ,
то ряд можнопочленно
интегрировать,
т. е.
,
то ряд можнопочленно
интегрировать,
т. е.
![]() выполняется равенство
выполняется равенство
 ,
,
причем полученный функциональный ряд тоже будет сходиться равномерно.
3. Если члены
сходящегося ряда
 непрерывно дифференцируемы на отрезке
непрерывно дифференцируемы на отрезке![]() ,
а ряд производных
,
а ряд производных равномерно сходится на отрезке
равномерно сходится на отрезке![]() ,
то ряд
,
то ряд сходится равномерно на отрезке
сходится равномерно на отрезке![]() и допускаетпочленное
дифференцирование,
т. е.
и допускаетпочленное
дифференцирование,
т. е.
 .
.
Пример 2.1. Доказать равномерную сходимость функциональных рядов в указанных промежутках:
а)
![]() на отрезке
на отрезке![]() ;
;
б)
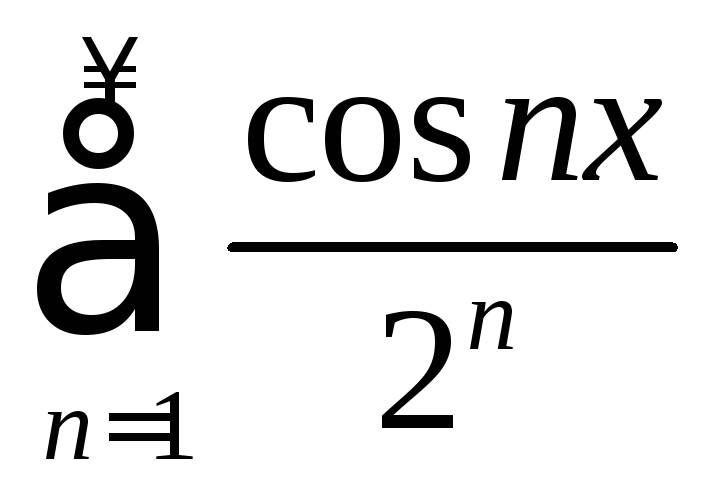 на всей числовой прямой;
на всей числовой прямой;
в)
 на всей числовой прямой.
на всей числовой прямой.
Решение. Воспользуемся признаком Вейерштрасса. Тогда:
а) Т. к. при
![]() выполняется неравенство
выполняется неравенство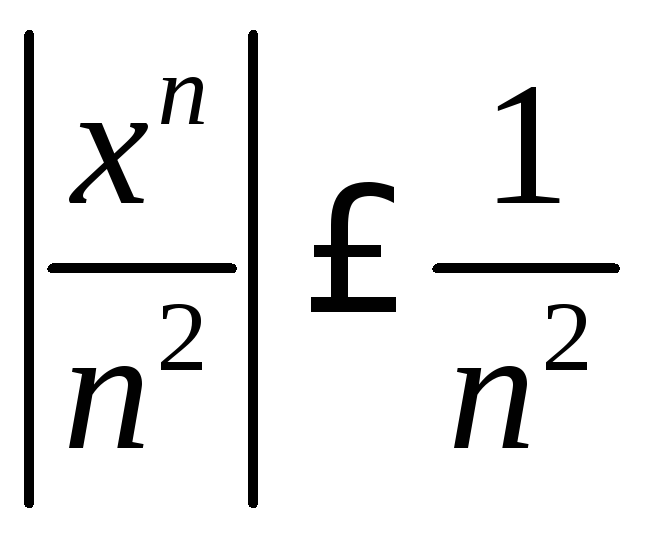 ,
а ряд
,
а ряд![]() сходится, то ряд
сходится, то ряд![]() равномерно и абсолютно сходится на
отрезке
равномерно и абсолютно сходится на
отрезке![]() .
.
б) Ряд
 равномерно и абсолютно сходится на всей
числовой прямой, т. к.
равномерно и абсолютно сходится на всей
числовой прямой, т. к. ,
а ряд
,
а ряд![]() сходится.
сходится.
в) Неравенство
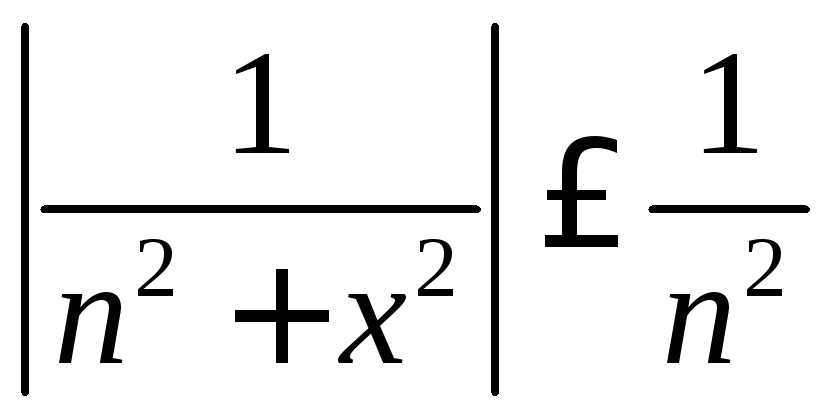 выполняется при любом
выполняется при любом![]() .
Числовой ряд
.
Числовой ряд![]() сходится. Следовательно, ряд
сходится. Следовательно, ряд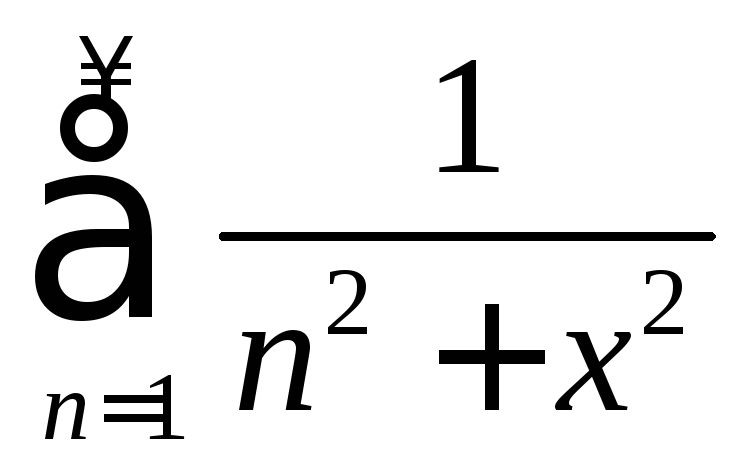 равномерно и абсолютно сходится на всей
числовой оси.
равномерно и абсолютно сходится на всей
числовой оси.
Пример 2.2. Найти область сходимости и абсолютной сходимости ряда:
а)
 ; б)
; б) .
.
Решение. а)
Обозначив
 ,
будем иметь
,
будем иметь
 .
.
На основании
признака Даламбера можно утверждать,
что ряд сходится абсолютно, если
![]() ,
т. е. при
,
т. е. при![]() ;
ряд расходится, если
;
ряд расходится, если![]() ,
т. е. если
,
т. е. если![]() .
При
.
При![]() получаем гармонический ряд
получаем гармонический ряд![]() ,
который расходится, а при
,
который расходится, а при![]() – ряд
– ряд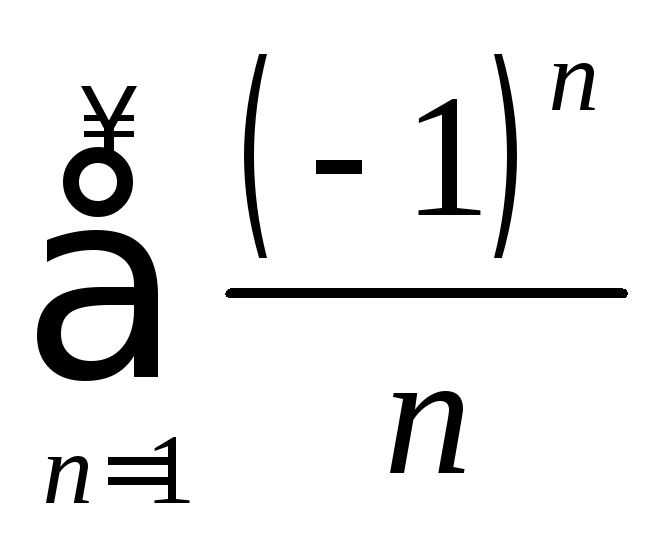 ,
который (по признаку Лейбница) сходится
условно.
,
который (по признаку Лейбница) сходится
условно.
Таким образом,

![]() область сходимости,
область сходимости,
![]() область абсолютной сходимости.
область абсолютной сходимости.
б) Обозначим
 .
Имеем
.
Имеем
 .
.
Ряд
 сходится абсолютно, если
сходится абсолютно, если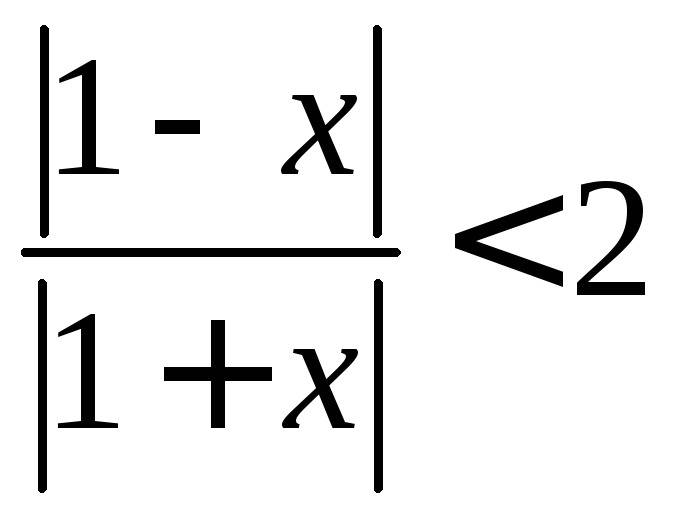 ,
т. е. при
,
т. е. при![]() ;
ряд расходится, если
;
ряд расходится, если![]() .
При
.
При![]() получаем ряд
получаем ряд![]() ,
а при
,
а при![]() – ряд
– ряд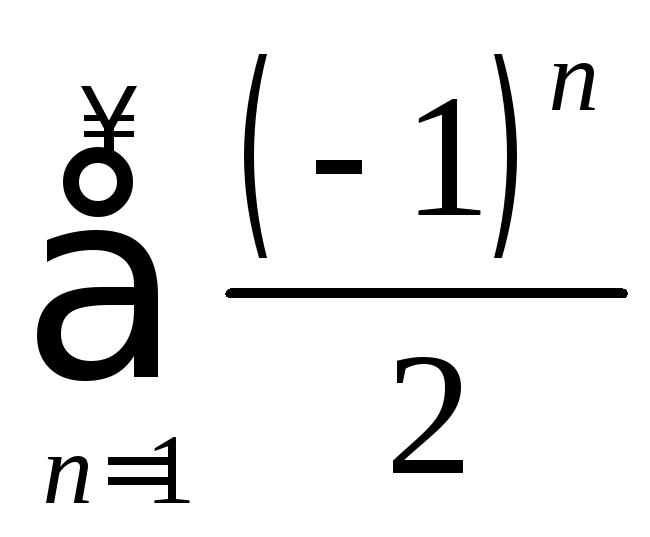 .
Оба ряда расходятся.
.
Оба ряда расходятся.
Таким образом,
![]()
![]() область сходимости и абсолютной
сходимости ряда.
область сходимости и абсолютной
сходимости ряда.
Пример 2.3.
Доказать,
что ряд
![]() не сходится равномерно в интервале
не сходится равномерно в интервале![]() ,
но сходится равномерно на всяком отрезке,
лежащем внутри этого интервала.
,
но сходится равномерно на всяком отрезке,
лежащем внутри этого интервала.
Решение.
Пользуясь формулой суммы геометрической
прогрессии, получим при
![]()
 .
.
Интервал
![]() содержит точки, сколь угодно близкие к
точке
содержит точки, сколь угодно близкие к
точке![]() ,
а так как
,
а так как ,
то, как бы велико ни было число
,
то, как бы велико ни было число![]() ,
найдутся точки
,
найдутся точки![]() ,
для которых
,
для которых![]() больше любого, сколь угодно большого
числа. Следовательно, нельзя подобрать
такое
больше любого, сколь угодно большого
числа. Следовательно, нельзя подобрать
такое![]() ,
чтобы при
,
чтобы при![]() неравенство
неравенство![]() имело место во всех точках интервала
имело место во всех точках интервала![]() .
Это означает, что сходимость ряда в
интервале
.
Это означает, что сходимость ряда в
интервале![]() не является равномерной.
не является равномерной.
Возьмем лежащий
внутри интервала
![]() отрезок
отрезок![]() ,
где
,
где![]() – сколь угодно малое положительное
число. На этом отрезке
– сколь угодно малое положительное
число. На этом отрезке![]() ,
следовательно,
,
следовательно,![]() .
Поскольку числовой ряд
.
Поскольку числовой ряд сходится, то, по признаку Вейерштрасса,
ряд
сходится, то, по признаку Вейерштрасса,
ряд![]() сходится абсолютно и равномерно на
любом отрезке
сходится абсолютно и равномерно на
любом отрезке![]() .
.
Найти область сходимости и область абсолютной сходимости функционального ряда:
|
2.1.
|
2.2.
|
|
2.3.
|
2.4.
|
|
2.5.
|
2.6.
|
|
2.7.
|
2.8.
|
|
2.9.
|
2.10.
|
Исходя из определения равномерной сходимости доказать равномерную сходимость функционального ряда в указанном промежутке:
|
2.11.
|
2.12.
| |
|
2.13.
|
| |
|
2.14.
|
| |
Пользуясь признаком Вейерштрасса, доказать равномерную сходимость функционального ряда в указанном промежутке:
|
2.15.
|
2.16.
|
|
2.17.
|
2.18.
|
|
2.19.
|
2.20.
|
|
2.21.
|
2.22.
|
Исследовать на сходимость и равномерную сходимость функциональный ряд в указанном промежутке:
|
2.23.
|
2.24.
|
|
2.25.
|
2.26.
|
Ответы: 2.1.
Сходится абсолютно при
![]() .2.2.
Сходится абсолютно при всех
.2.2.
Сходится абсолютно при всех
![]() .2.3.
Сходится абсолютно при
.2.3.
Сходится абсолютно при
![]() .2.4.
Сходится абсолютно при
.2.4.
Сходится абсолютно при
![]() .2.5.
Сходится абсолютно при
.2.5.
Сходится абсолютно при
![]() ,
сходится условно при
,
сходится условно при![]() .2.6.
Сходится абсолютно на отрезках
.2.6.
Сходится абсолютно на отрезках
![]() ,
,![]() .2.7.
Сходится абсолютно при
.2.7.
Сходится абсолютно при
![]() .2.8.
Сходится абсолютно при
.2.8.
Сходится абсолютно при
![]() .2.9.
Сходится абсолютно при
.2.9.
Сходится абсолютно при
![]() .2.10.
Сходится абсолютно при
.2.10.
Сходится абсолютно при
![]() .2.23.
Сходится равномерно. 2.24.
Сходится равномерно. 2.25.
Сходится равномерно. 2.26.
Сходится равномерно.
.2.23.
Сходится равномерно. 2.24.
Сходится равномерно. 2.25.
Сходится равномерно. 2.26.
Сходится равномерно.

 .
.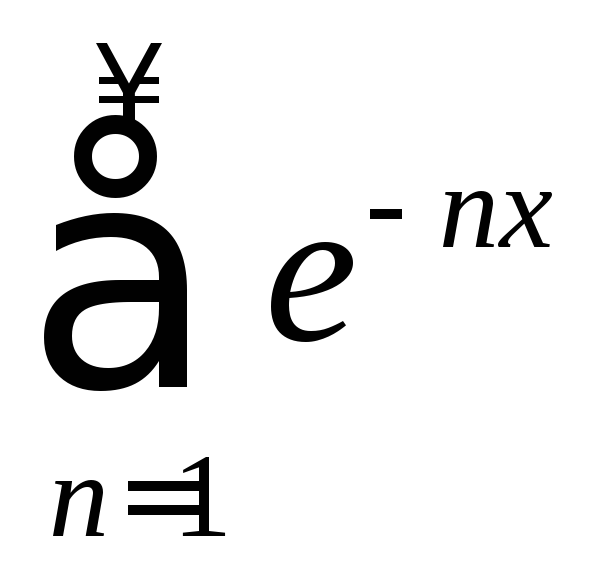 .
. .
.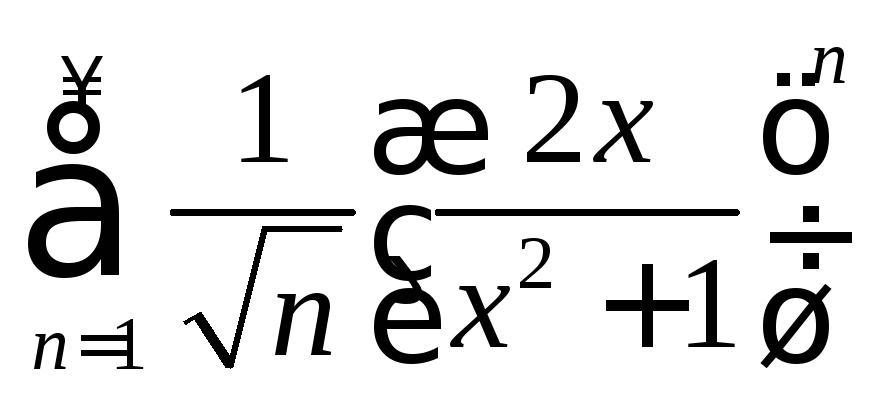 .
. .
. .
. .
. .
. .
.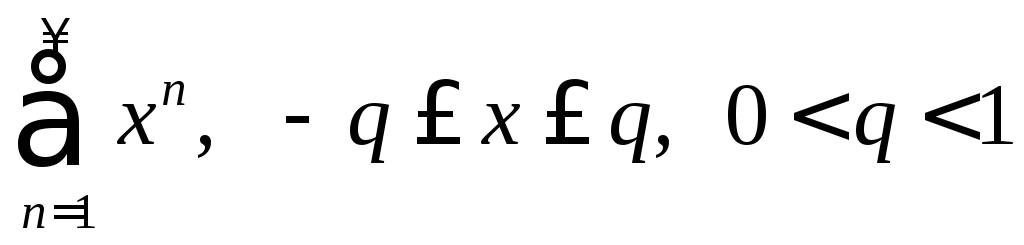 .
. .
. .
. .
. .
. .
. .
. .
.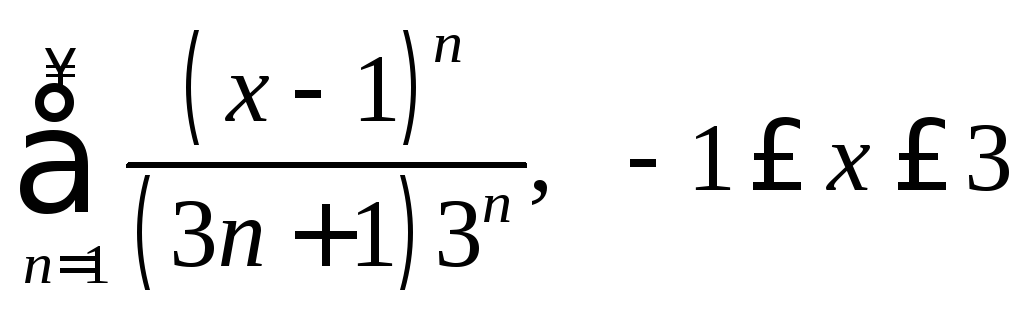 .
. .
. .
. .
. .
. .
.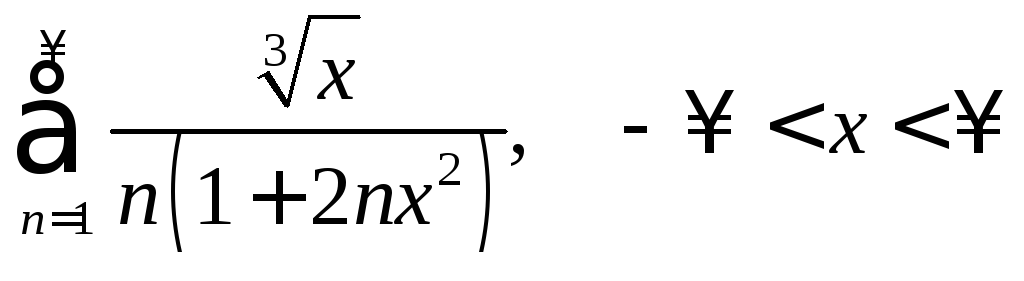 .
. .
.