
- •III. Ряды
- •1.2. Ряды с неотрицательными членами
- •Найти все значения , при которых сходится ряд :
- •Исследовать на сходимость ряд с помощью признака Даламбера:
- •Исследовать на сходимость ряд с помощью признака Коши:
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость
- •§ 2. Функциональные ряды
- •2.1. Признаки сходимости функциональных рядов
- •Свойства функциональных рядов
- •2.2. Степенные ряды
- •Ряды Тейлора и Маклорена
- •Разложение основных элементарных функций в ряд Маклорена
- •§ 3. Тригонометрические ряды Фурье
III. Ряды
§ 1. Числовые ряды
1.1. Основные понятия
Числовой
ряд
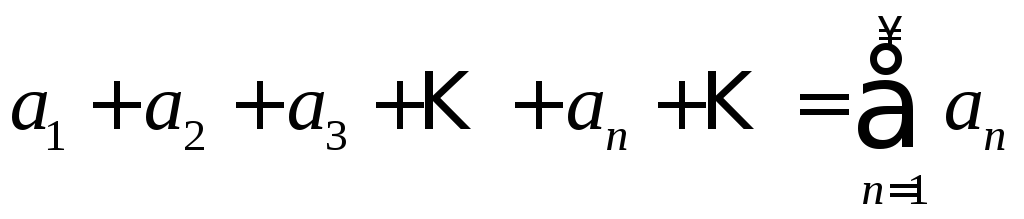 называется сходящимся,
или
суммируемым,
если
его частичные
суммы
называется сходящимся,
или
суммируемым,
если
его частичные
суммы
![]()
имеют
предел при
![]() .
.
Величина
![]() называется суммой ряда, а число
называется суммой ряда, а число
![]() называется остатком
ряда
(тоже
ряд).
называется остатком
ряда
(тоже
ряд).
Если
![]() не существует либо он бесконечен, то
рядрасходится.
не существует либо он бесконечен, то
рядрасходится.
Ряд сходится тогда
и только тогда, когда для любого
![]() остаток
остаток![]() сходится.
сходится.
Необходимый
признак сходимости.
Если ряд
![]() сходится, то
сходится, то![]() .
Обратное утверждение неверно.
.
Обратное утверждение неверно.
Достаточный
признак расходимости. Если
![]() ,
то ряд
,
то ряд![]() расходится.
расходится.
Свойства
сходящихся рядов. Пусть
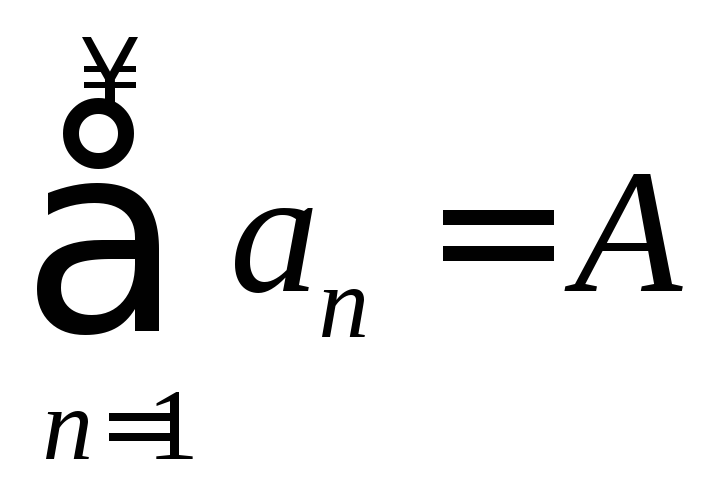 ,
,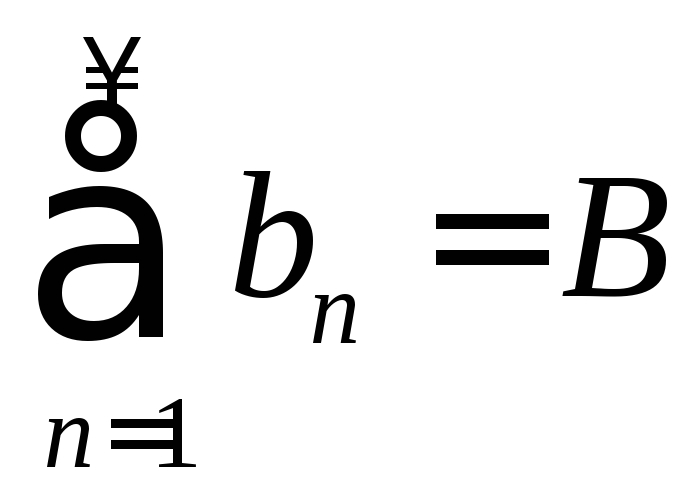 и
и![]() – постоянная величина. Тогда
– постоянная величина. Тогда
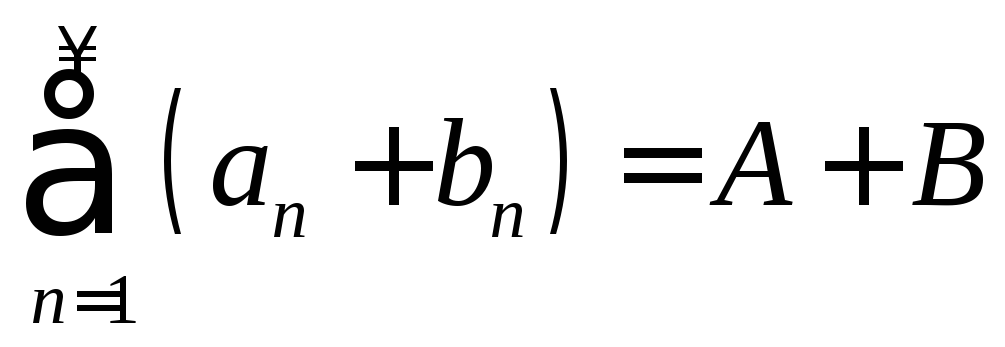 ;
;
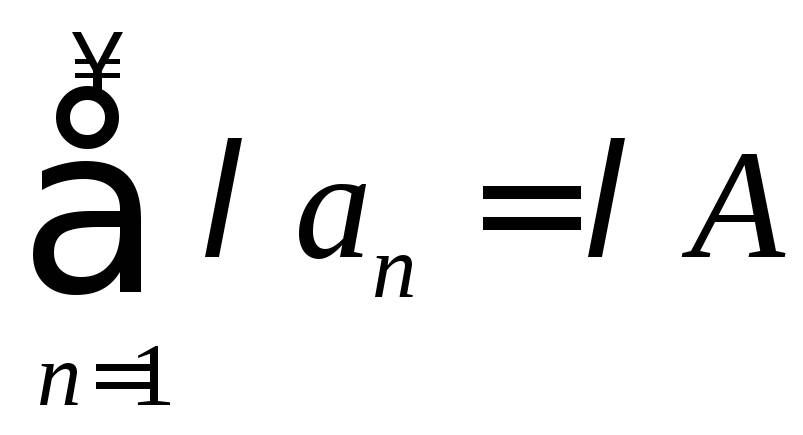 .
.
Если ряд сходится, то сходятся также и другие ряды, полученные из исходного ряда добавлением, удалением или перестановкой конечного числа членов. (Сумма ряда может измениться).
Критерий Коши.
Для сходимости
ряда
![]() необходимо и достаточно, чтобы для
всякого положительного числа
необходимо и достаточно, чтобы для
всякого положительного числа![]() можно было подобрать такое
можно было подобрать такое![]() ,
чтобы при
,
чтобы при![]() и любом положительном
и любом положительном![]() выполнялось неравенство
выполнялось неравенство![]() .
.
Пример 1.1. Исследовать сходимость рядов:
а)
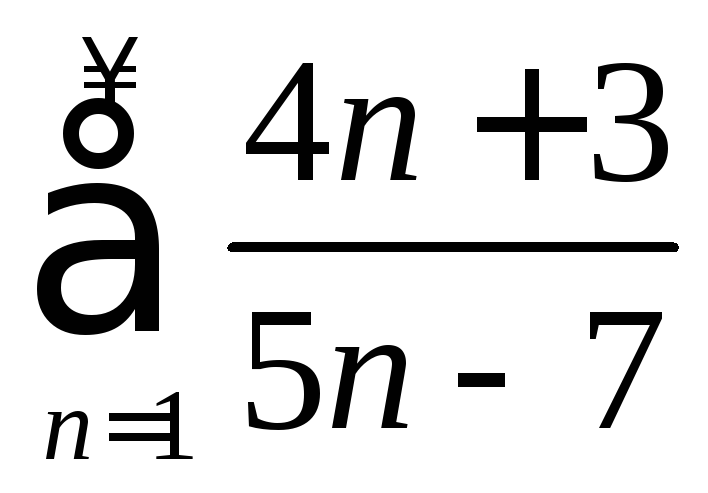 ; б)
; б)![]() .
.
Решение. а) Проверим выполнение необходимого признака сходимости:
![]() .
.
Необходимый признак сходимости не выполняется, следовательно, ряд расходится.
б) Ряд
![]() называетсягармоническим.
Очевидно,
называетсягармоническим.
Очевидно,
![]() ,
т. е. общий член стремится к нулю. Покажем,
что этот ряд расходится. Используем
критерий Коши. Следует доказать, что
,
т. е. общий член стремится к нулю. Покажем,
что этот ряд расходится. Используем
критерий Коши. Следует доказать, что![]()
![]() .
.
В качестве
![]() выберем число
выберем число
![]() .
Берем любое
.
Берем любое
![]() и любое
и любое![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда
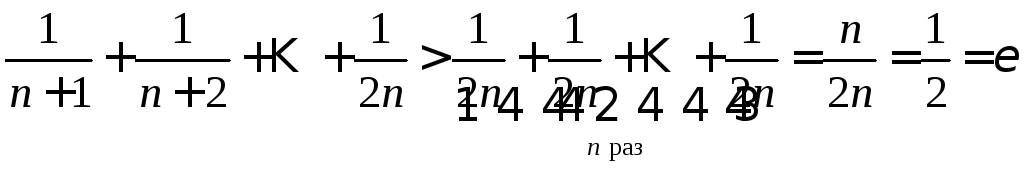 .
.
Пример 1.2.
Исследовать
на сходимость ряд
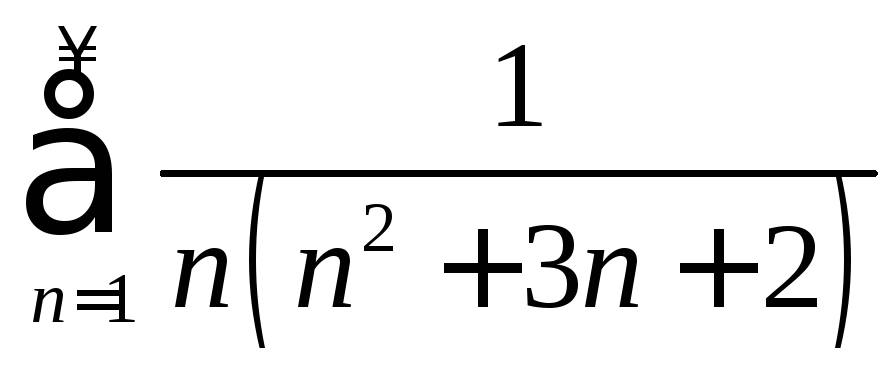 и найти его сумму.
и найти его сумму.
Решение. Используя
метод неопределенных коэффициентов,
представим общий член ряда
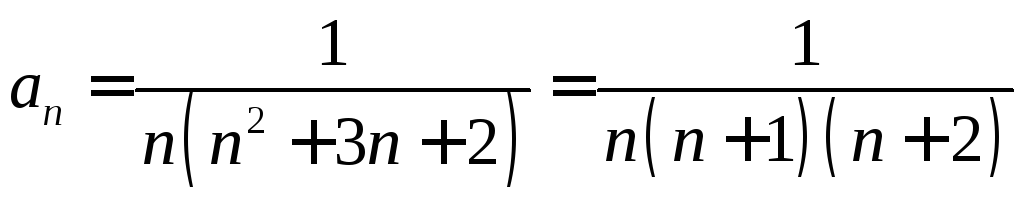 в виде суммы простейших дробей:
в виде суммы простейших дробей:
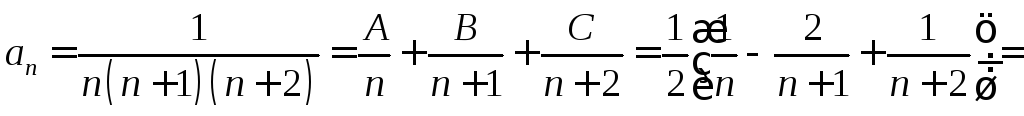
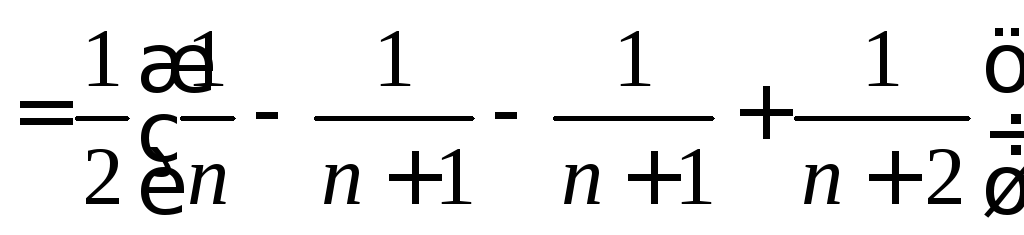 .
.
Таким образом,

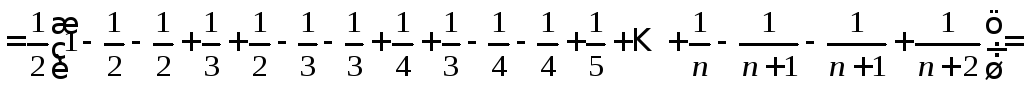
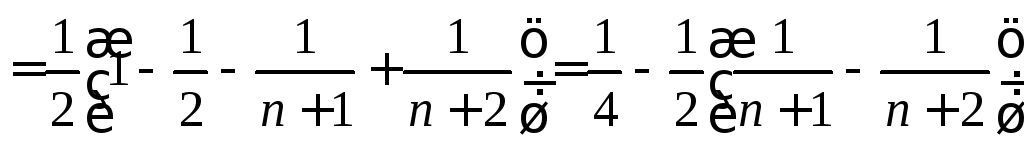 .
.
Так как
![]() ,
данный ряд сходится и его сумма равна
,
данный ряд сходится и его сумма равна![]() .
.
Пример 1.3.
Пусть
![]() .
Доказать, что ряды
.
Доказать, что ряды
а)
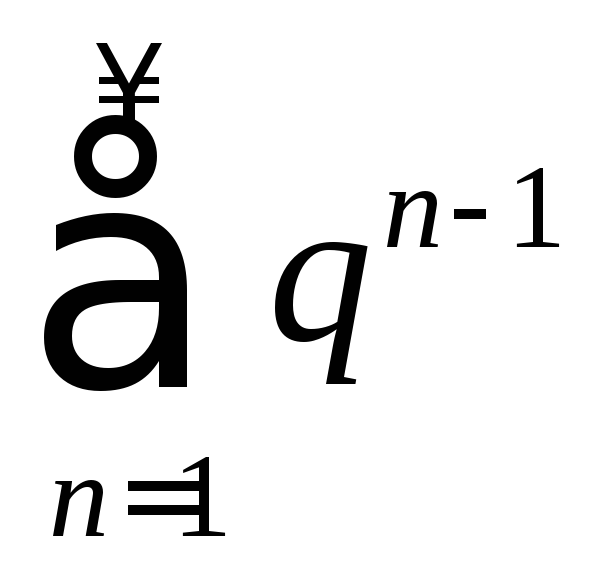 ; б)
; б)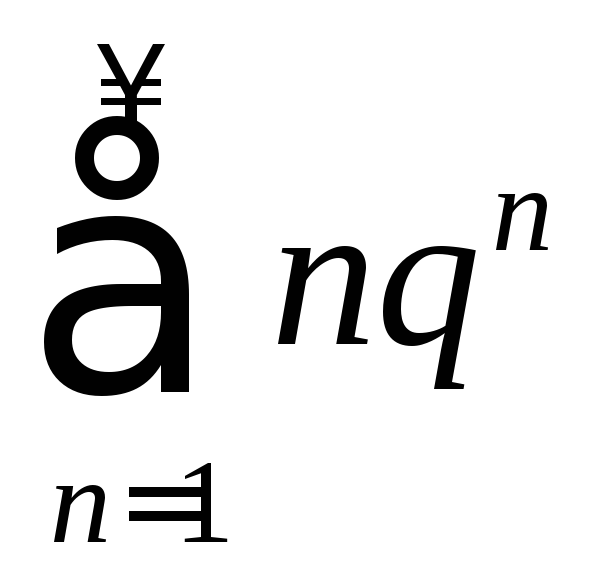
сходятся и найти их суммы.
Решение. а)
Используя формулы для суммы
![]() первых членов геометрической прогрессии,
получаем
первых членов геометрической прогрессии,
получаем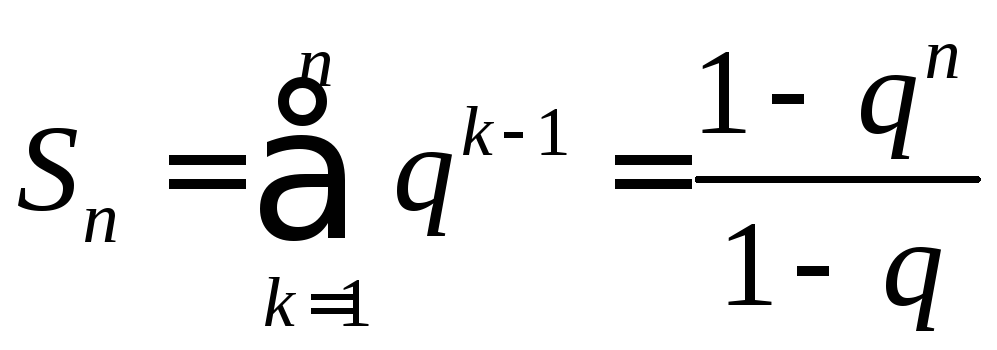 ,
откуда следует, что
,
откуда следует, что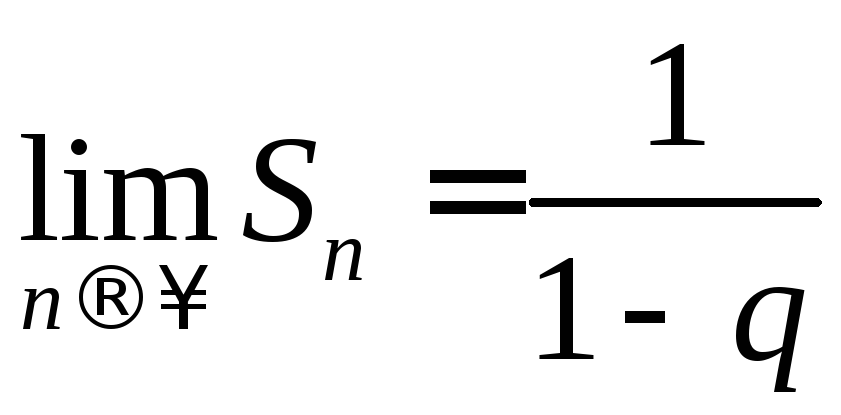 .
Итак,
.
Итак,
 ,
,
![]() .
.
б) Так как
 ,
то
,
то
![]()
![]()
![]() .
.
Откуда
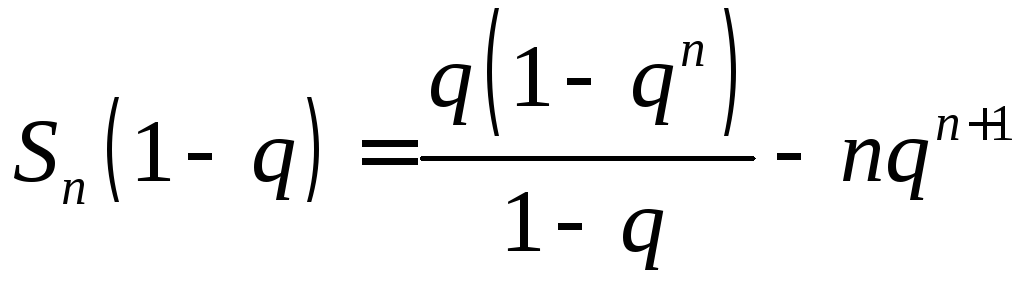 ;
;
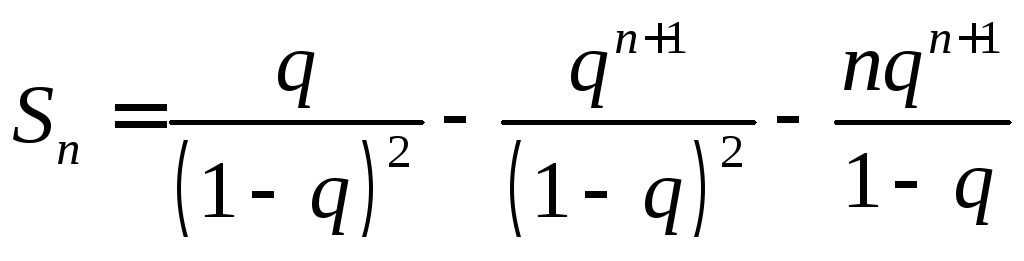 .
.
Если
![]() ,
то
,
то![]() ;
поэтому существует
;
поэтому существует ,
т. е.
,
т. е.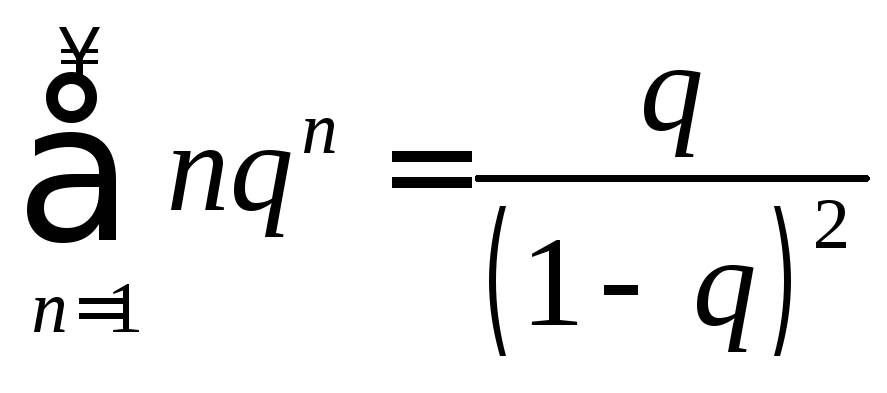 .
.
Найти
![]() -ю
частичную сумму
-ю
частичную сумму![]() ряда и сумму
ряда и сумму![]() этого ряда:
этого ряда:
|
1.1.
|
1.2.
|
|
1.3.
|
1.4.
|
|
1.5.
|
1.6.
|
|
1.7.
|
1.8.
|
|
1.9.
|
1.10.
|
|
1.11.
|
1.12.
|
Доказать расходимость ряда, используя необходимое условие сходимости:
|
1.13.
|
1.14.
|
|
1.15.
|
1.16.
|
|
1.17.
|
1.18.
|
|
1.19.
|
1.20.
|
Пользуясь критерием
Коши, доказать сходимость ряда
![]() ,
если:
,
если:
|
1.21.
|
1.22.
|
|
1.23.
|
1.24.
|
Пользуясь критерием
Коши, доказать расходимость ряда
![]() ,
если:
,
если:
|
1.25.
|
1.26.
|
|
1.27.
|
1.28.
|
Ответы: 1.1. 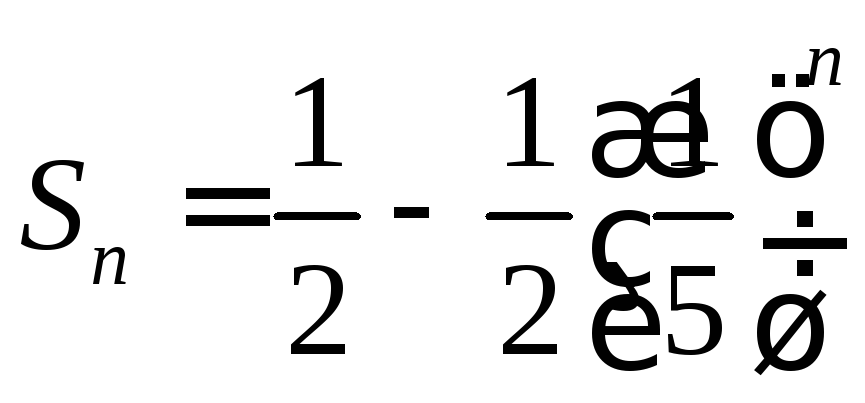 ,
,![]() .1.2.
.1.2. 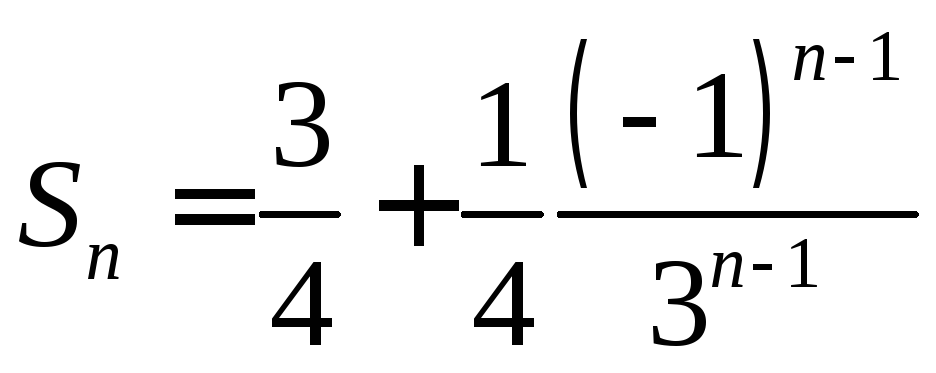 ,
,![]() .1.3.
.1.3. ![]() ,
,![]() .1.4.
.1.4. 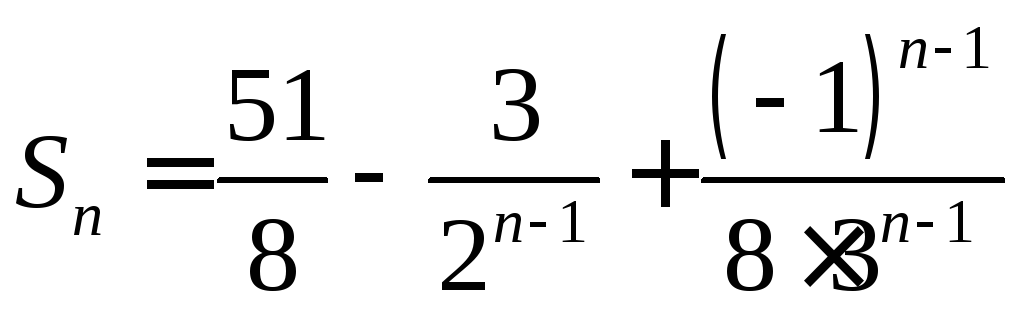 ,
,![]() .1.5.
.1.5. ![]() ,
,![]() .1.6.
.1.6. 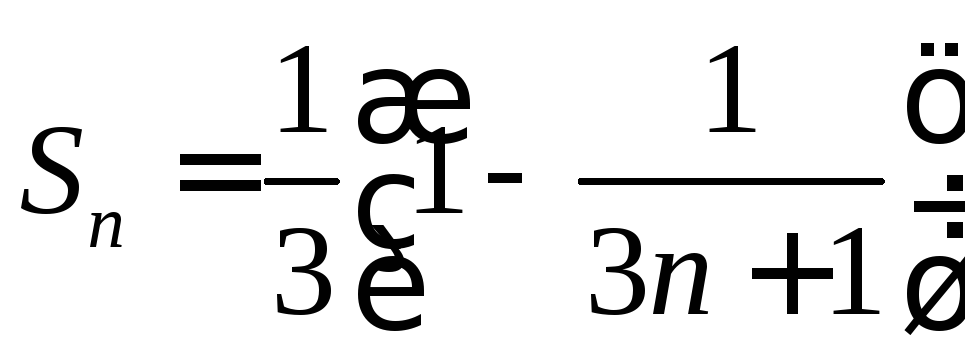 ,
,![]() .
.
1.7. 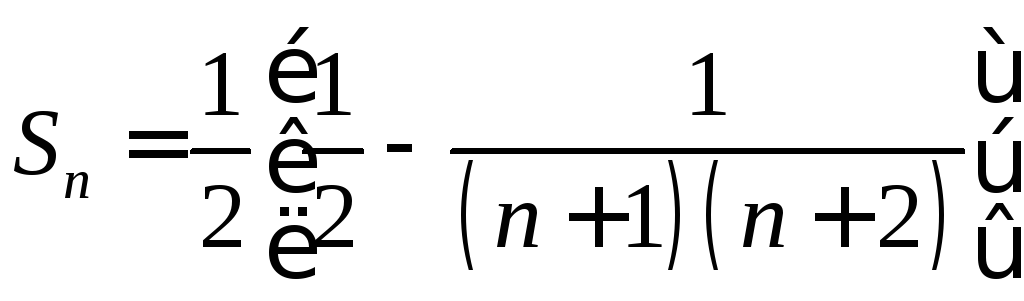 ,
,![]() .1.8.
.1.8.  ,
,
![]() .
1.9.
.
1.9.
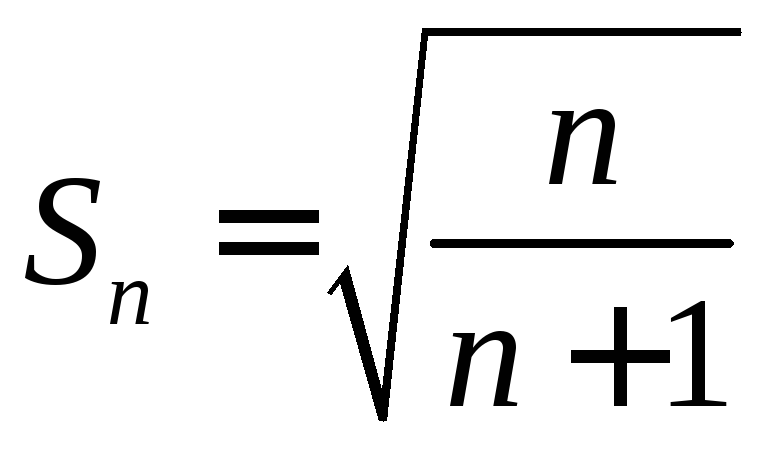 ,
,![]() .1.10.
.1.10.
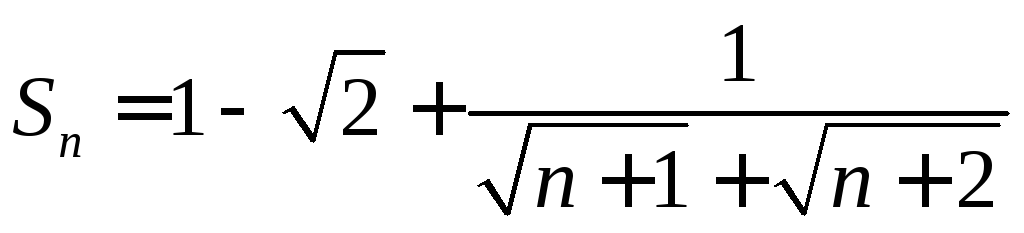 ,
,
![]() .
1.11.
.
1.11.
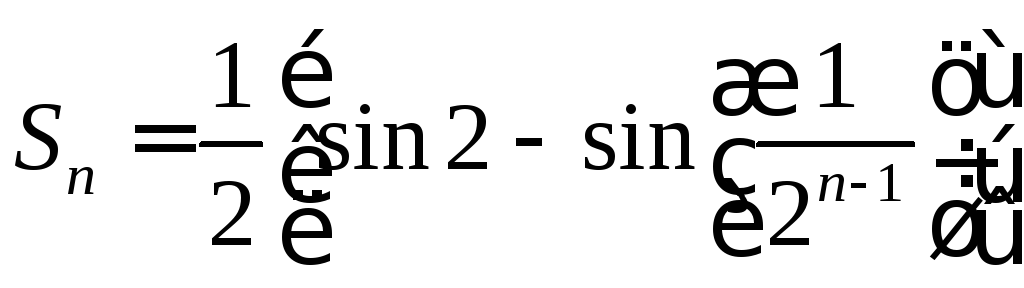 ,
,![]() .1.12.
.1.12. ![]() ,
,
![]() .
.
1.2. Ряды с неотрицательными членами
Если все члены
ряда
![]() имеют, начиная
с некоторого номера, постоянный знак,
то такой ряд называется знакопостоянным.
Для определенности
будем считать, что все
имеют, начиная
с некоторого номера, постоянный знак,
то такой ряд называется знакопостоянным.
Для определенности
будем считать, что все
![]() .
Тогда частичные суммы
.
Тогда частичные суммы![]() ряда
ряда
![]() образуют монотонно возрастающую
последовательность.
образуют монотонно возрастающую
последовательность.
Критерий
сходимости рядов с неотрицательными
членами.
Для сходимости ряда
![]() ,
где
,
где
![]() ,
необходимо и достаточно, чтобы
последовательность его частичных сумм
была ограничена.
,
необходимо и достаточно, чтобы
последовательность его частичных сумм
была ограничена.
Признак сравнения
I.
Если, начиная с некоторого номера,
выполняется неравенство
![]() ,
то из сходимости ряда
,
то из сходимости ряда![]() следует сходимость ряда
следует сходимость ряда
![]() ,
а из расходимостиряда
,
а из расходимостиряда
![]() следует расходимость ряда
следует расходимость ряда
![]() .
.
Признак сравнения
II.
Пусть
![]() и
и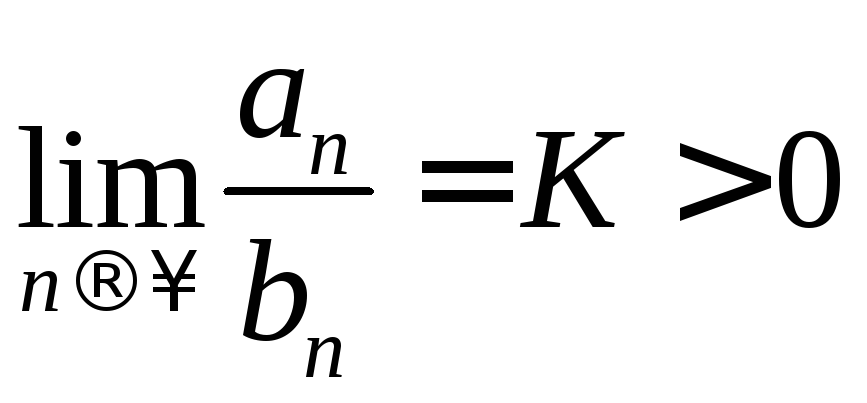 .
Тогда ряды
.
Тогда ряды
![]() и
и
![]() сходятся или расходятся одновременно.
(То есть невозможно, чтобы один из них
сходился, а другой расходился).
сходятся или расходятся одновременно.
(То есть невозможно, чтобы один из них
сходился, а другой расходился).
В качестве «эталонных» рядов обычно используют:
1) геометрический
ряд
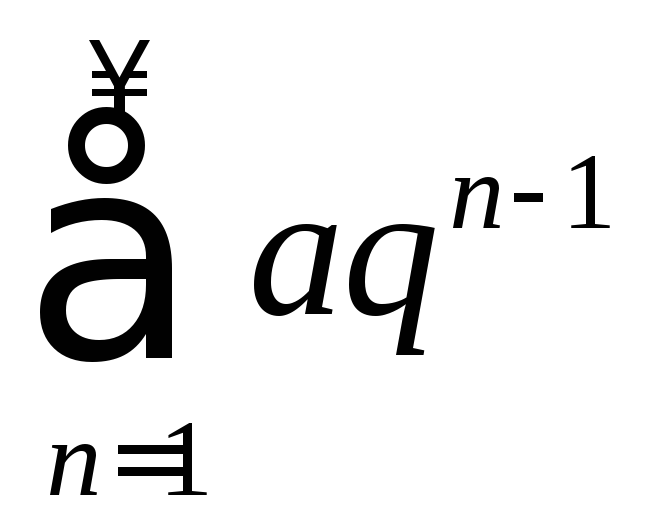 ,
который сходится при
,
который сходится при![]() и
расходится при
и
расходится при![]() ;
;
2) обобщенный
гармонический ряд
![]() ,
который сходится при
,
который сходится при![]() и расходится при
и расходится при![]() .
.
Метод выделения
главной части.
Если для ряда
![]() с неотрицательными членами удается
получить асимптотическую формулу вида
с неотрицательными членами удается
получить асимптотическую формулу вида![]() ,
то ряд сходится при
,
то ряд сходится при![]() и расходится при
и расходится при![]() .
.
Признак Коши.
Пусть существует
![]() .
Тогда если
.
Тогда если
![]() – ряд сходится, если
– ряд сходится, если![]() – ряд расходится, если
– ряд расходится, если![]() – признак неприменим.
– признак неприменим.
Признак
Даламбера.
Если существует
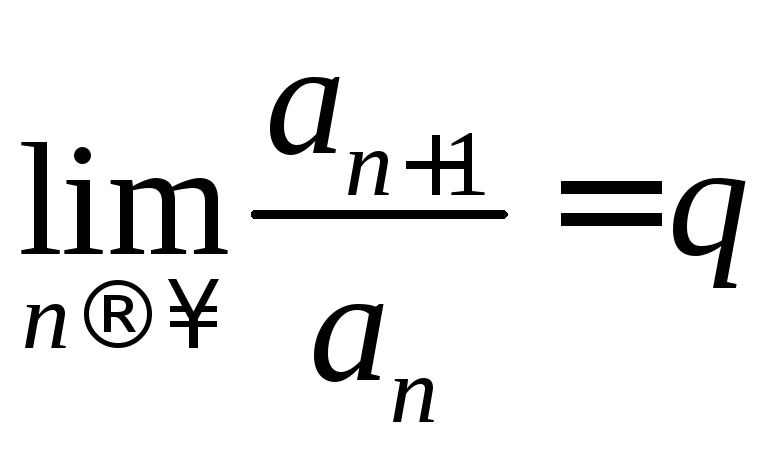 ,
то при
,
то при![]() ряд сходится, при
ряд сходится, при![]() – расходится, а при
– расходится, а при![]() признак неприменим.
признак неприменим.
Признак Раабе.
Если
![]() и существует
и существует ,
то при
,
то при![]() ряд
ряд![]() сходится, а при
сходится, а при![]() – расходится.
– расходится.
Признак Гаусса.
Пусть
![]() и
и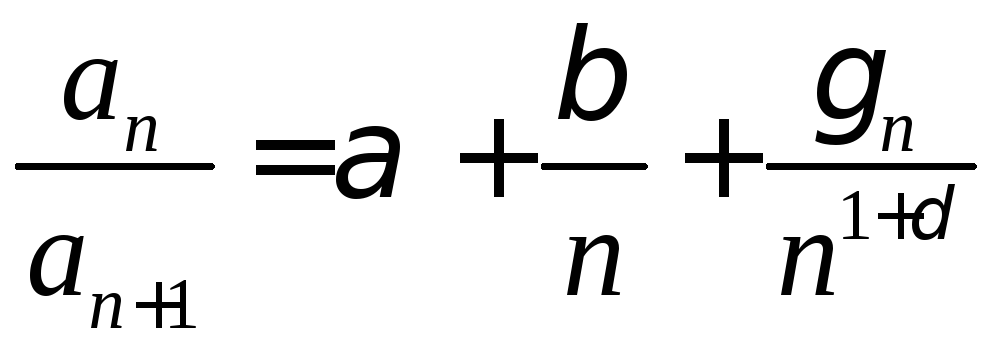 ,
где
,
где![]() .
.
|
Тогда: |
если
если
если
если
|
Интегральный
признак Коши-Маклорена.
Пусть
![]() – непрерывная, неотрицательная, монотонно
убывающая функция, определенная при
– непрерывная, неотрицательная, монотонно
убывающая функция, определенная при![]() .
Тогда ряд
.
Тогда ряд и интеграл
и интеграл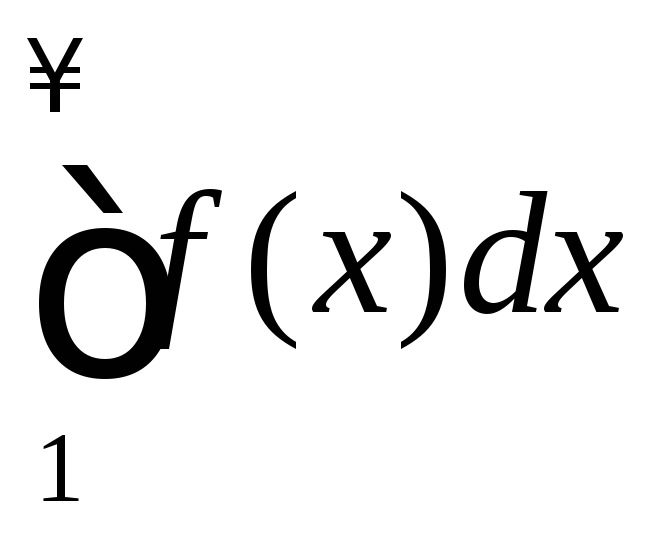 либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Пример 1.4. Исследовать сходимость рядов:
а)
 ; б)
; б)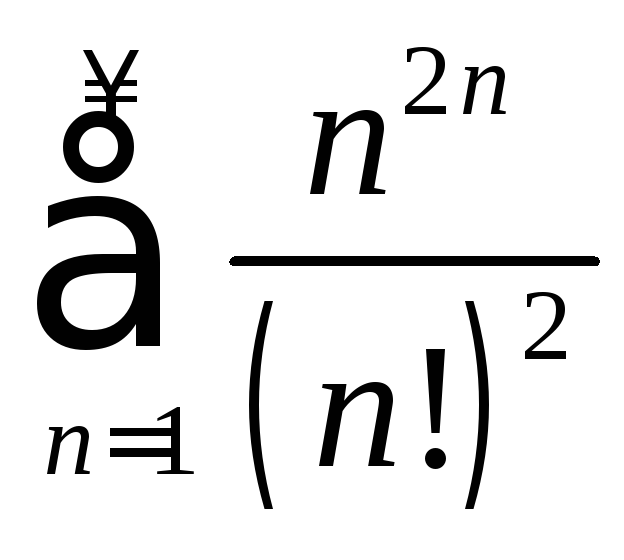 ;
;
в)
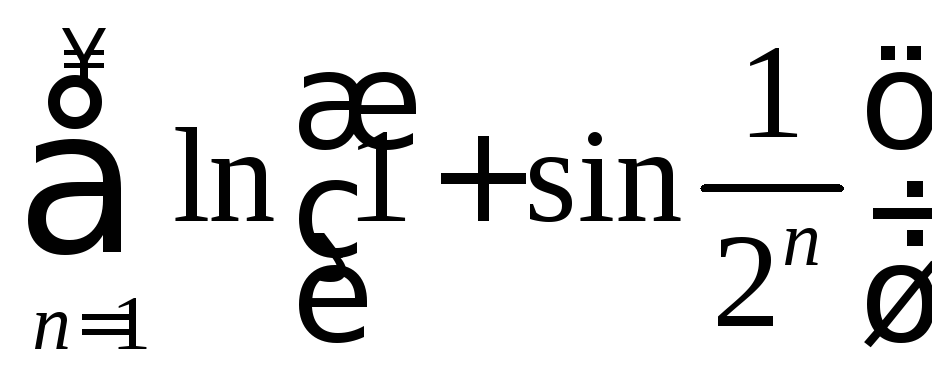 ;
г)
;
г)
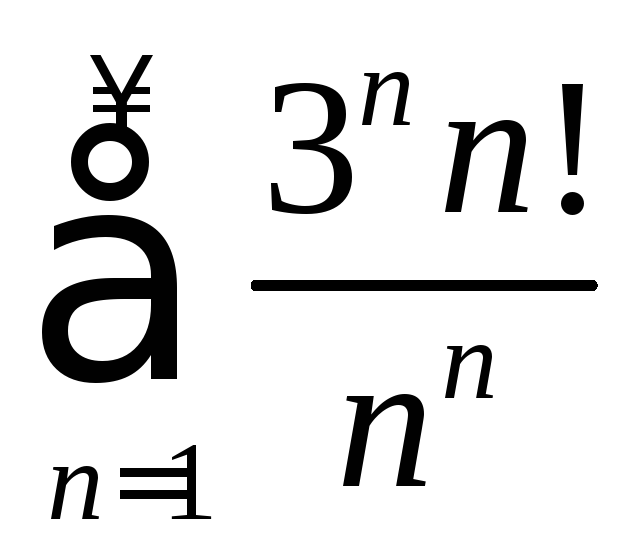 .
.
Решение. а) Используем признак Коши:

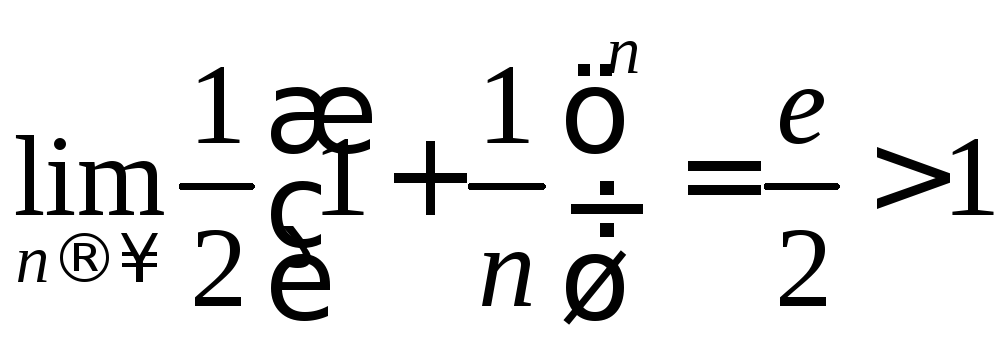 .
.
Ряд расходится.
б) Используя
асимптотическую формулу Стирлинга
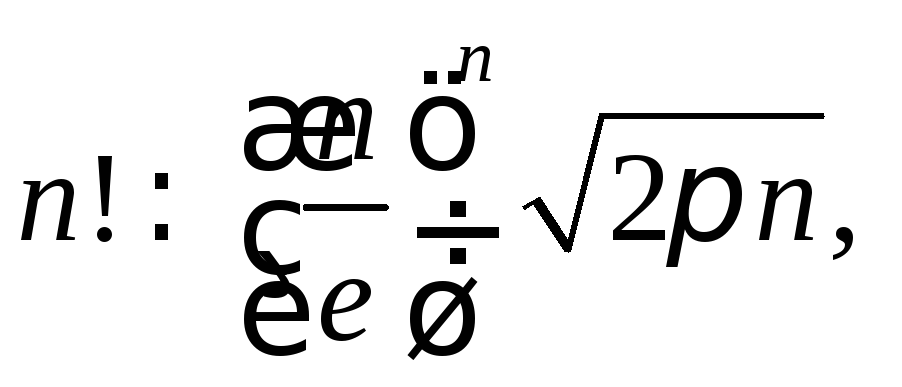 при
при![]() получим
получим
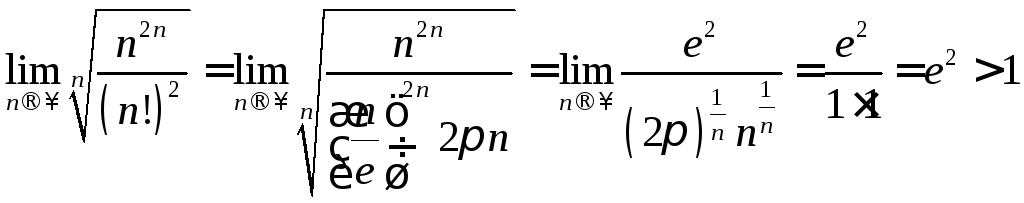 .
.
Следовательно, ряд расходится.
в) Ряд
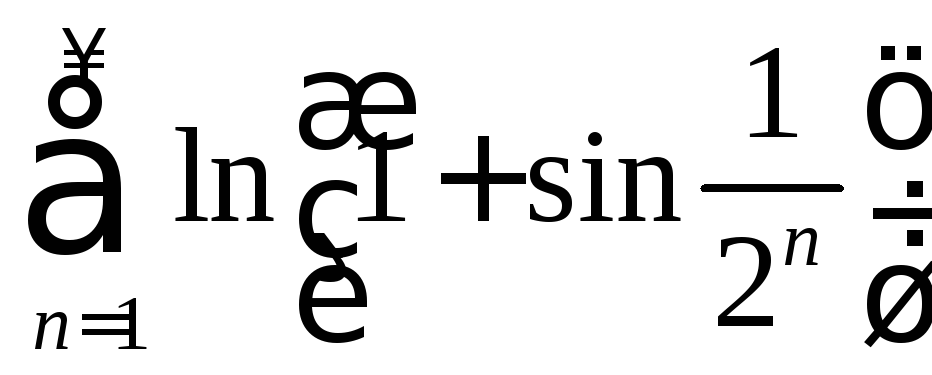 сходится, т.
к. при
сходится, т.
к. при
![]()
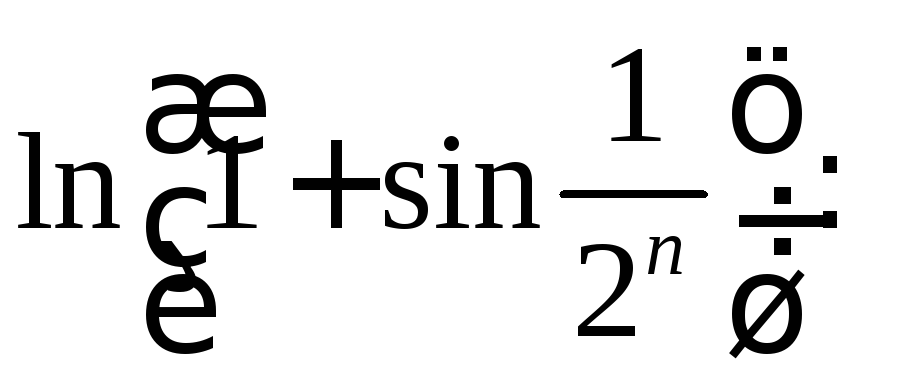
![]() ,
,![]() ,
и ряд
,
и ряд
![]() сходится.
сходится.
г) Имеем
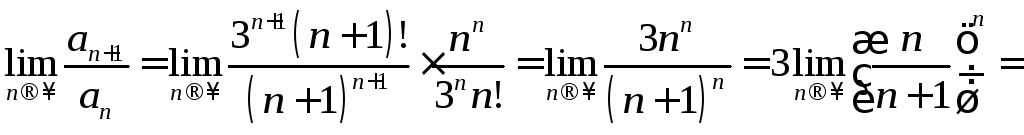
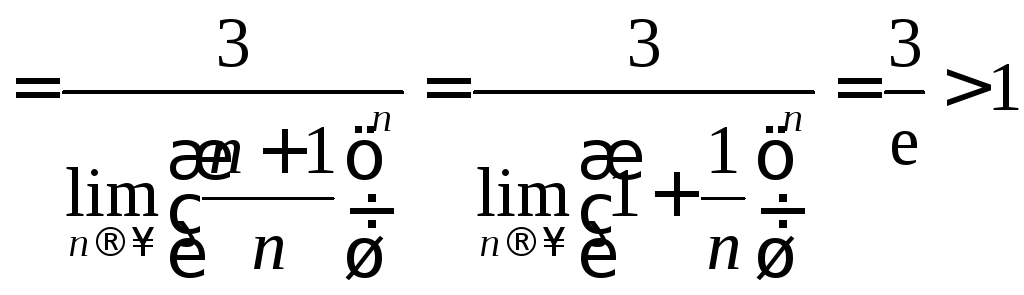 ;
;
поэтому ряд расходится.
Пример 1.5. Исследовать сходимость рядов:
а)
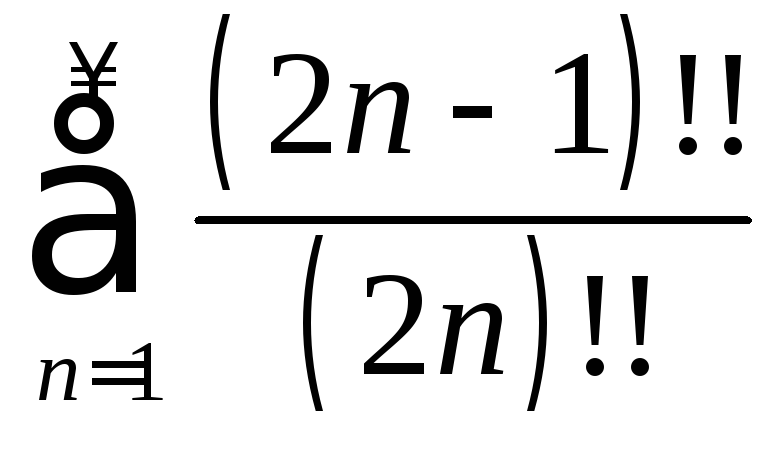 ; б)
; б)![]() ;
;
в)
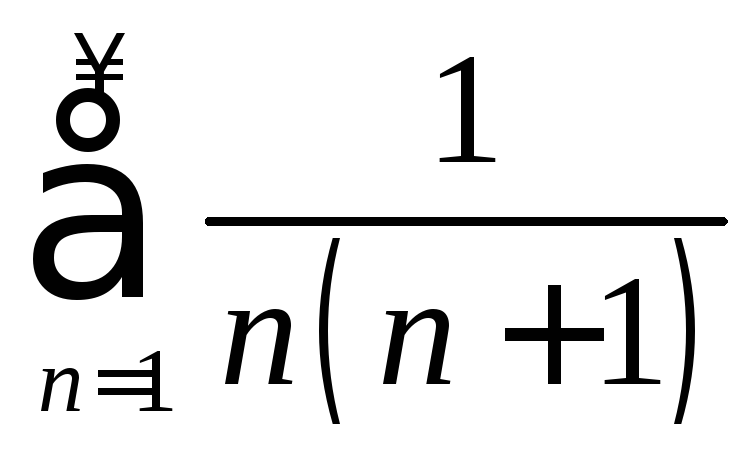 ; г)
; г)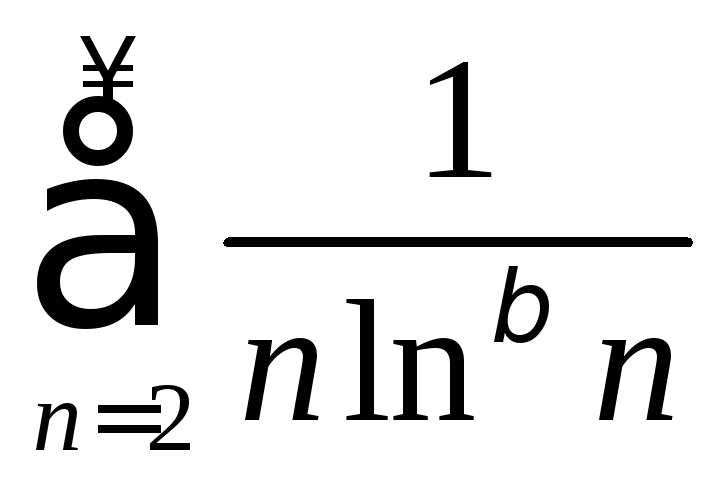 .
.
Решение. а)
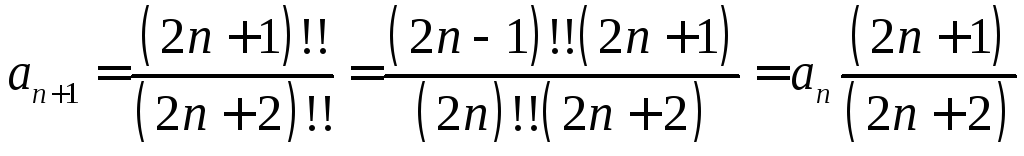 .
Воспользуемся признаком Раабе
.
Воспользуемся признаком Раабе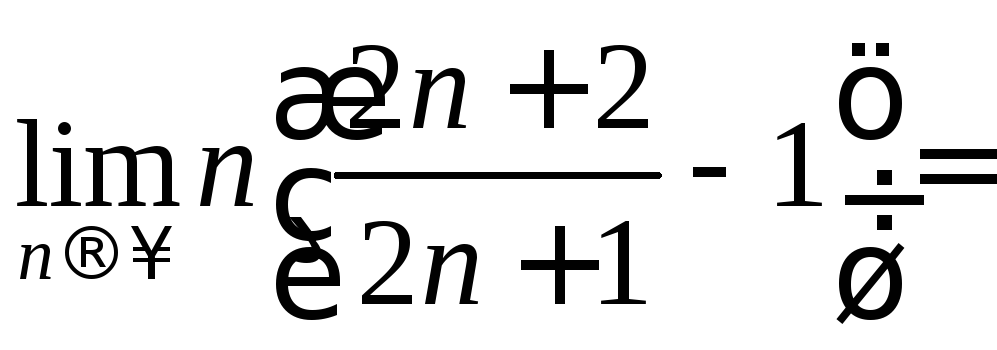
![]() .
Ряд расходится.
.
Ряд расходится.
б) В применении к
ряду
![]() признак Гаусса дает
признак Гаусса дает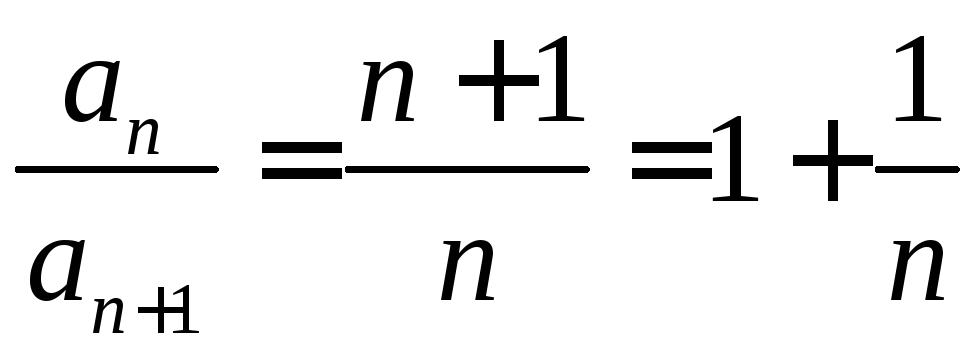 ;
;![]() — ряд расходится.
— ряд расходится.
в) Для
ряда
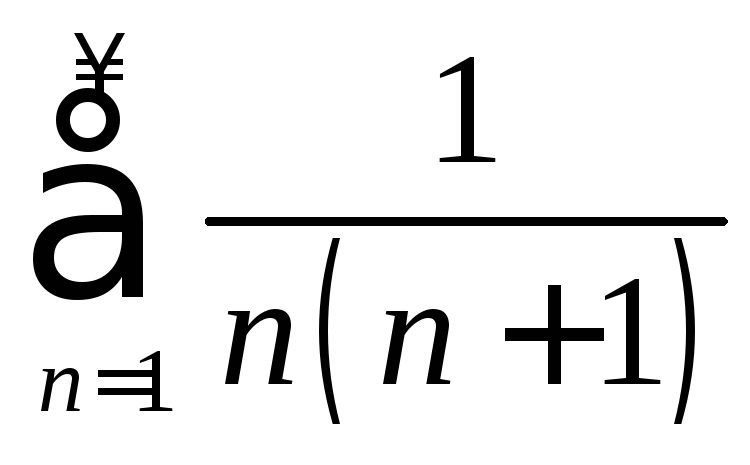 имеем
имеем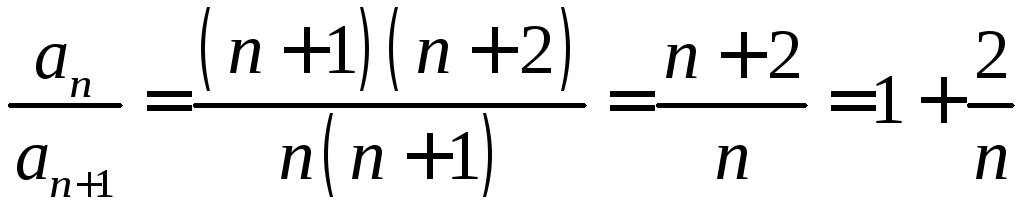 ;
;![]() ,
,![]() – ряд сходится.
– ряд сходится.
г) Введем
функцию
![]() и рассмотрим несобственный интеграл
и рассмотрим несобственный интеграл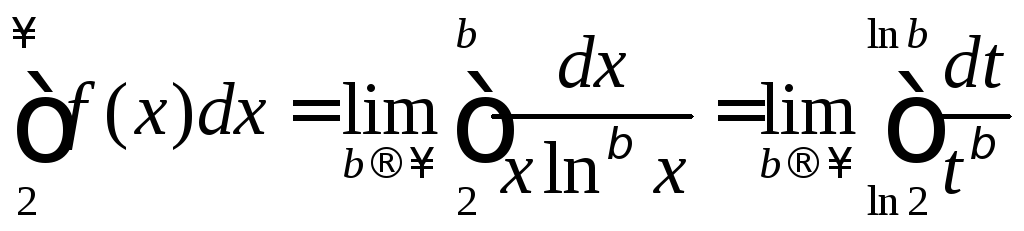 .
Из последнего равенства видно, что
данный интеграл сходится, если
.
Из последнего равенства видно, что
данный интеграл сходится, если![]() ,
и расходится, если
,
и расходится, если![]() .
.
Доказать сходимость
ряда
![]() ,
установив ограниченность сверху
последовательности его частичных сумм:
,
установив ограниченность сверху
последовательности его частичных сумм:
|
1.29.
|
1.30.
|
|
1.31.
|
1.32.
|
Исследовать
сходимость ряда
![]() ,
использовав признаки сравнения или
получив асимптотическую формулу вида
,
использовав признаки сравнения или
получив асимптотическую формулу вида![]() ,
при
,
при![]() .
.
|
1.33.
|
1.34.
|
|
1.35.
|
1.36.
|
|
1.37.
|
1.38.
|
|
1.39.
|
1.40.
|
|
1.41.
|
1.42.
|
|
1.43.
|
1.44.
|
|
1.45.
|
1.46.
|
|
1.47.
|
1.48.
|
|
1.49.
|
1.50.
|
|
1.51.
|
1.52.
|

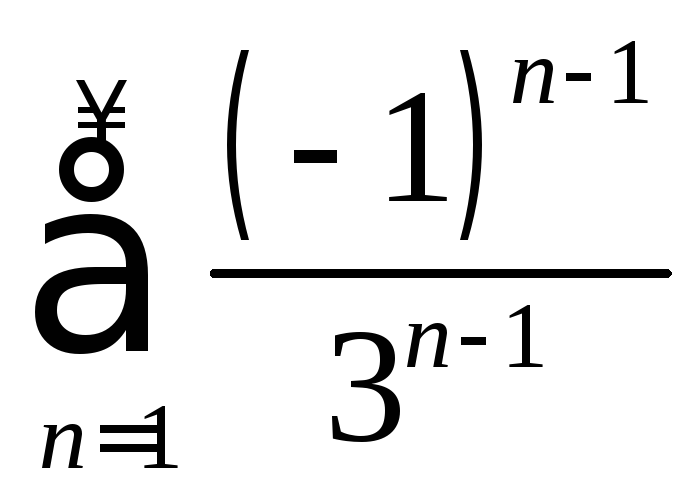 .
.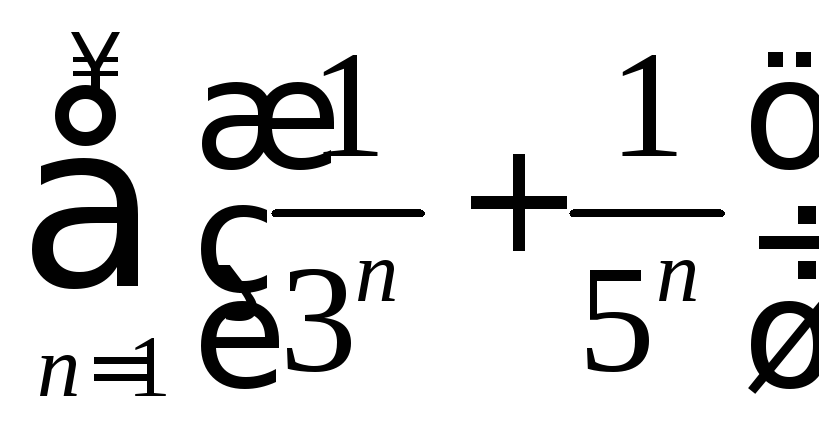 .
.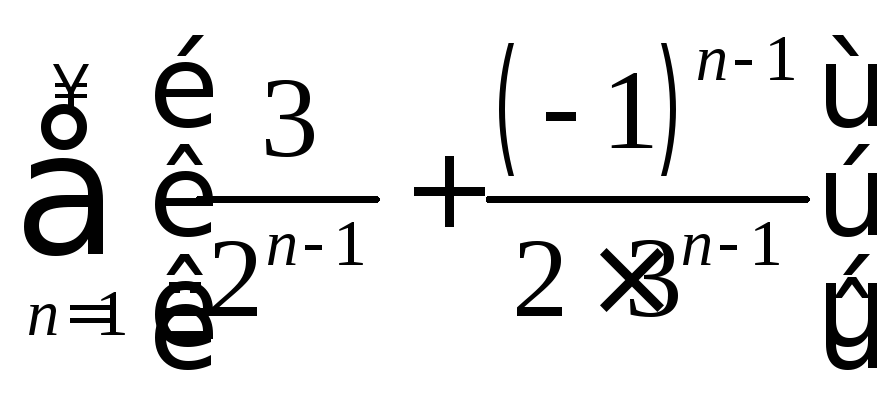 .
.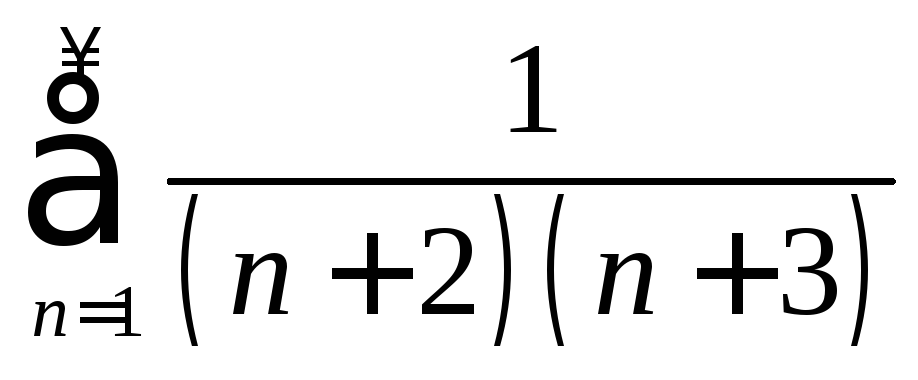 .
.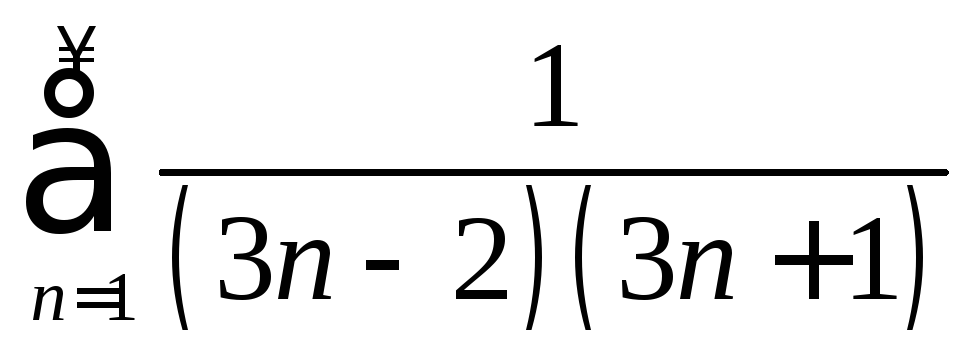 .
.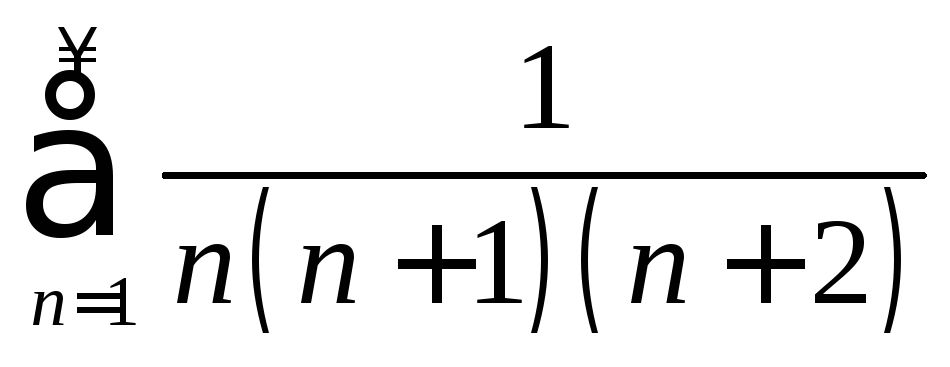 .
.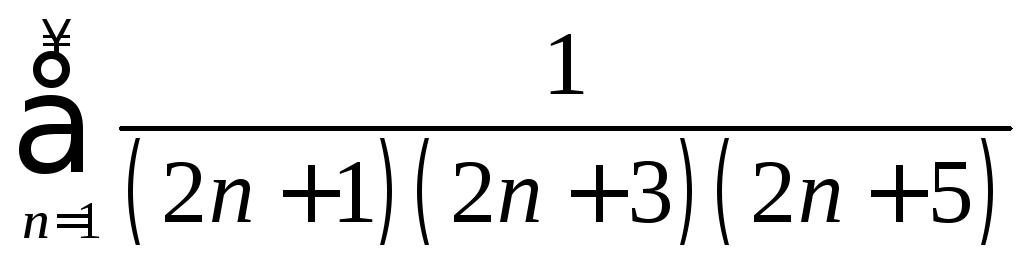 .
.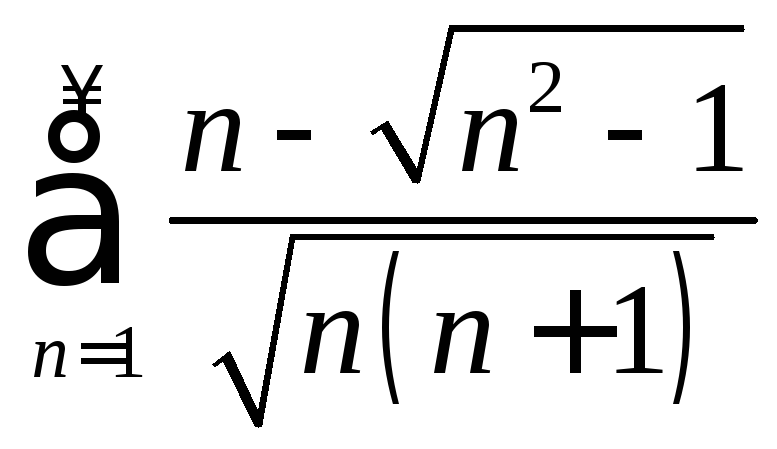 .
.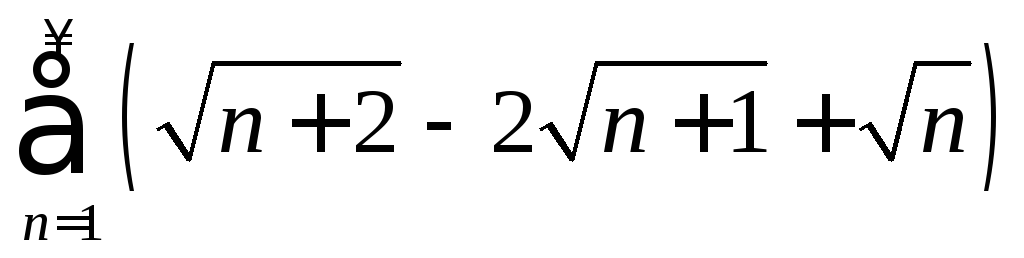 .
.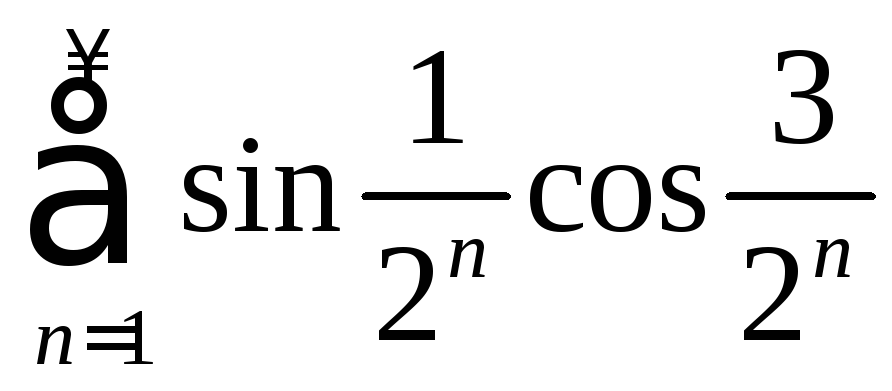 .
.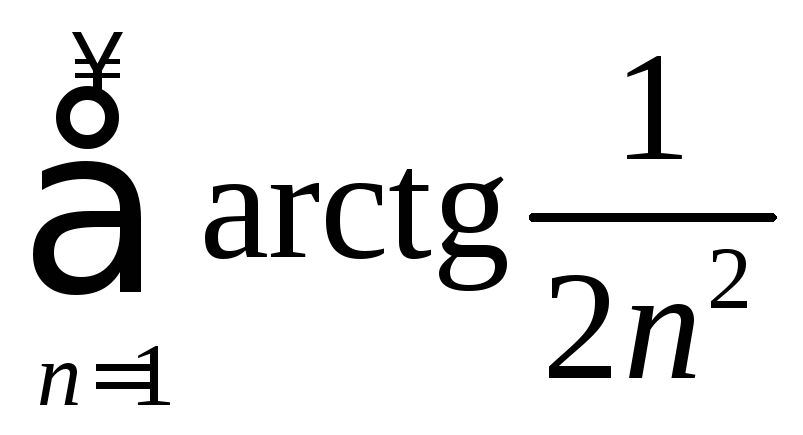 .
. .
.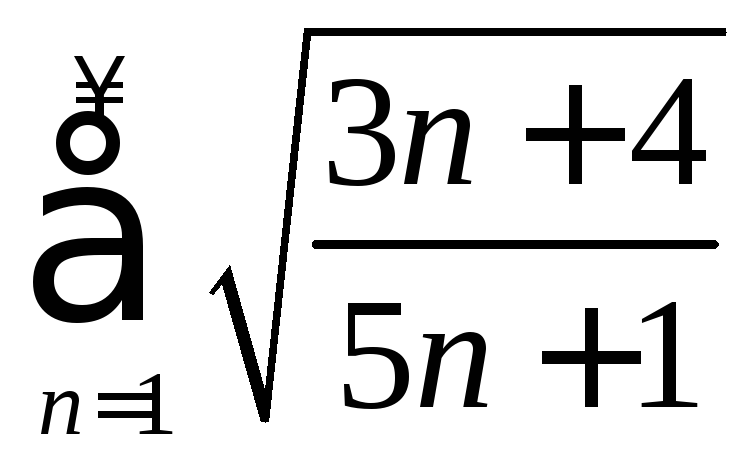 .
.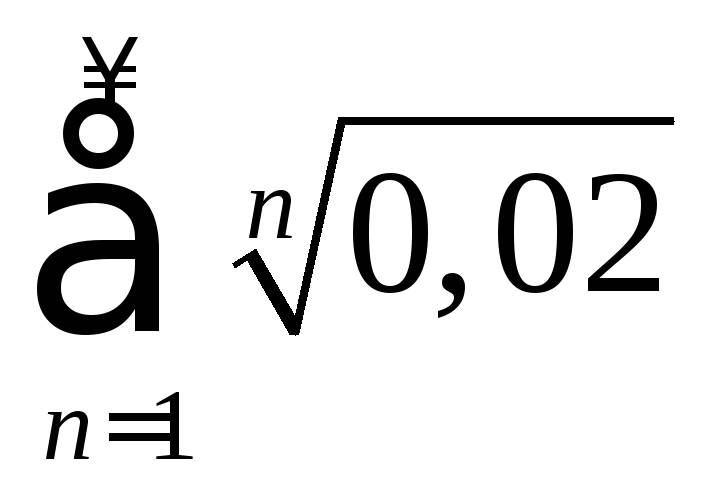 .
. .
.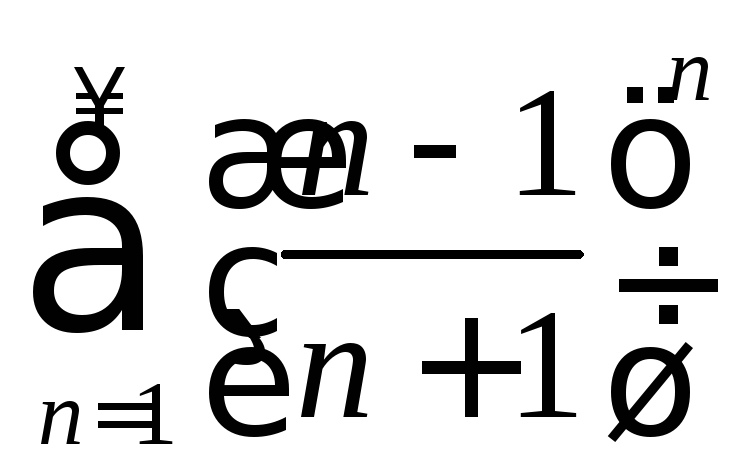 .
.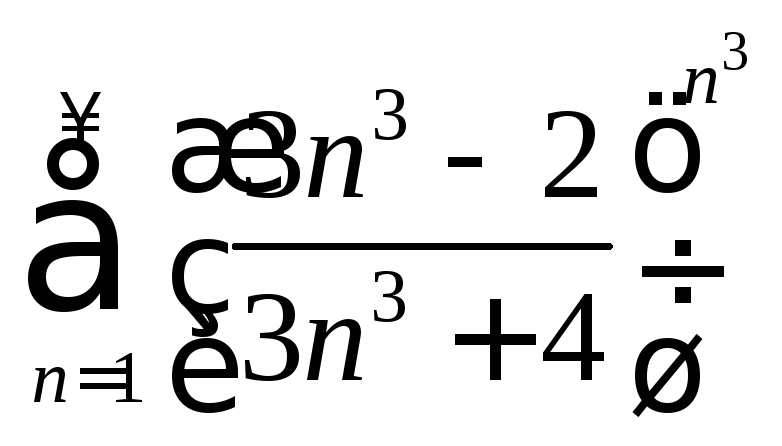 .
.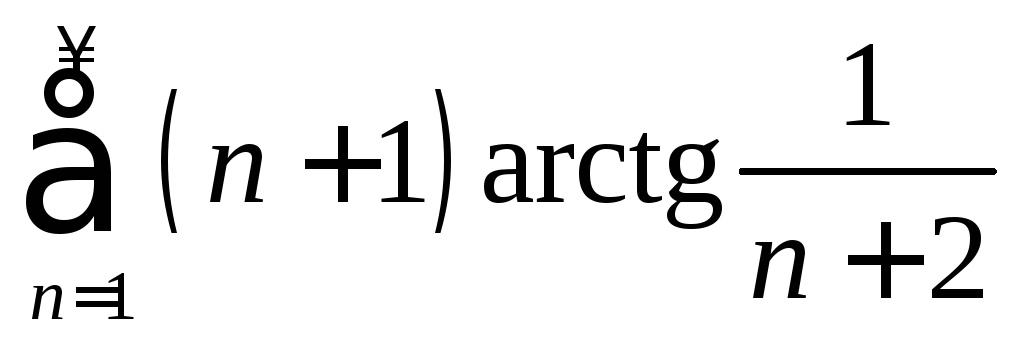 .
.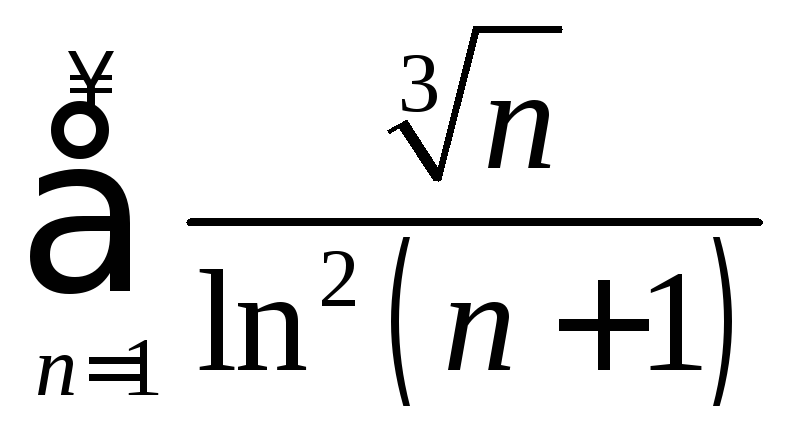 .
. .
.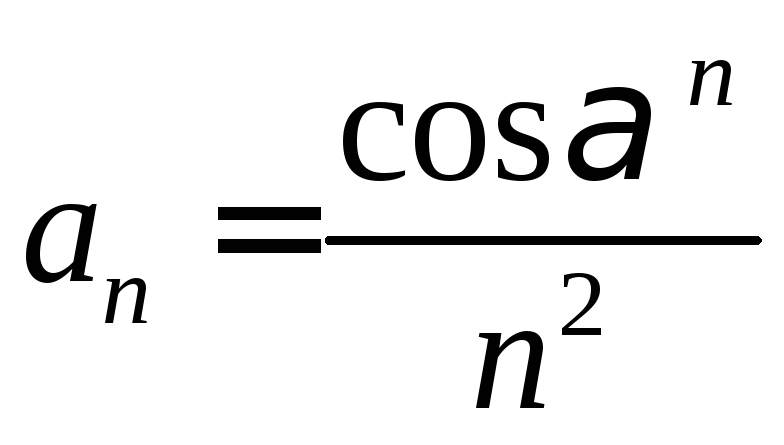 .
.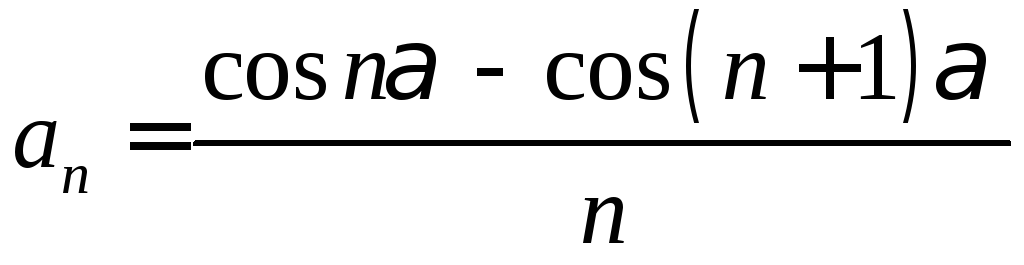 .
.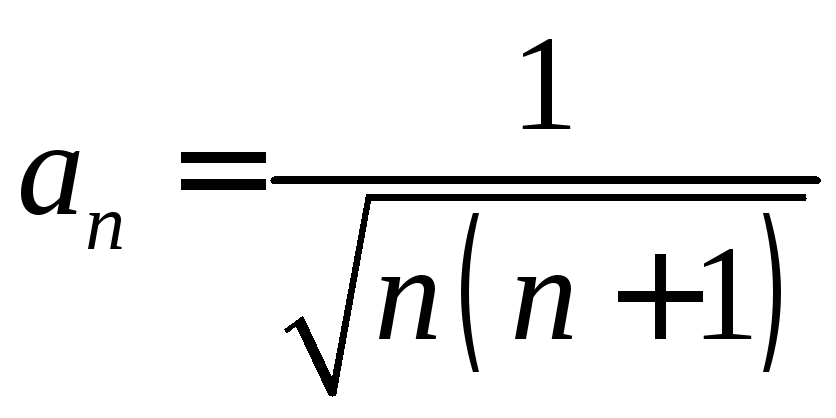 .
. .
.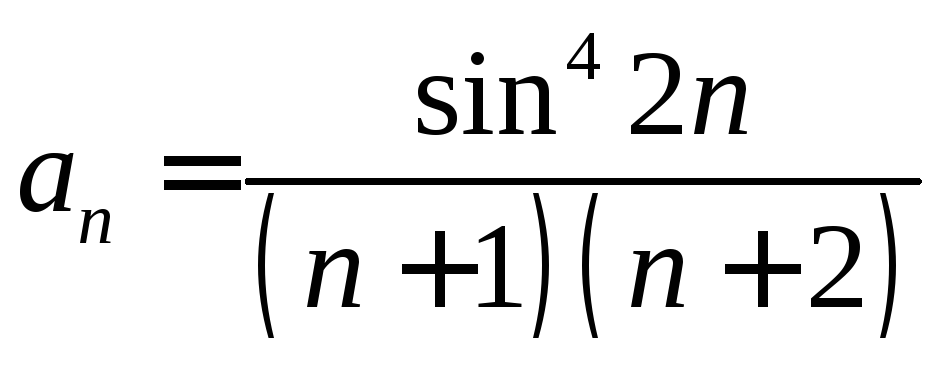 .
.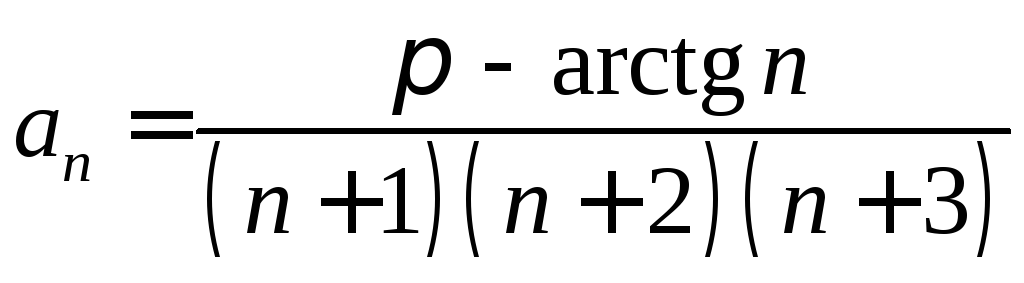 .
.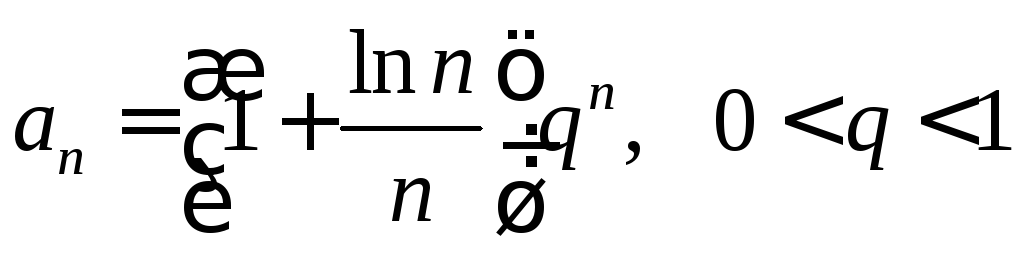 .
. .
. .
.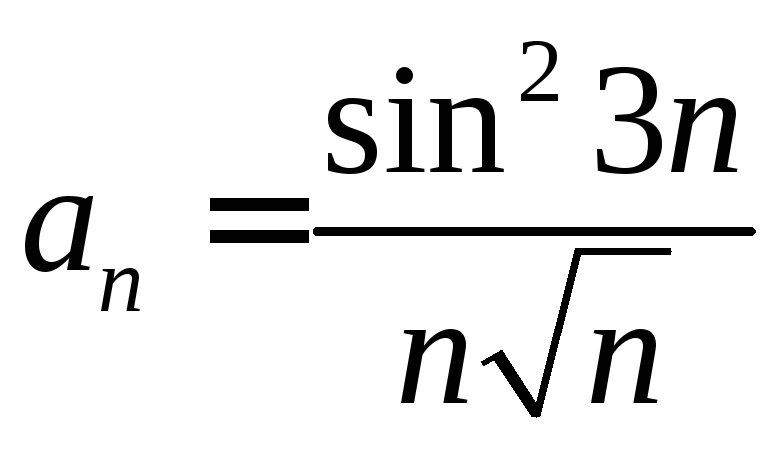 .
. .
.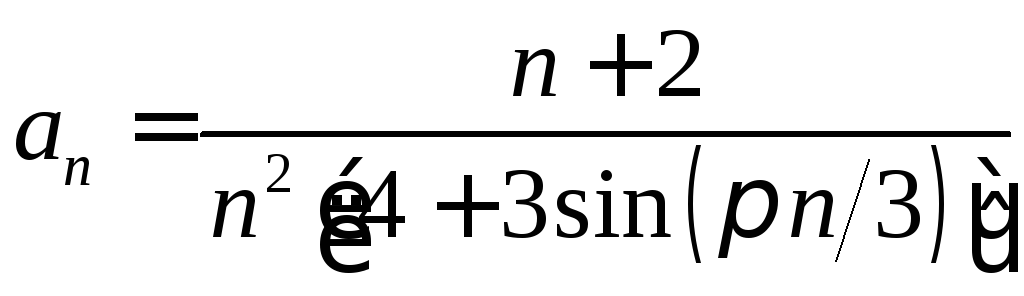 .
.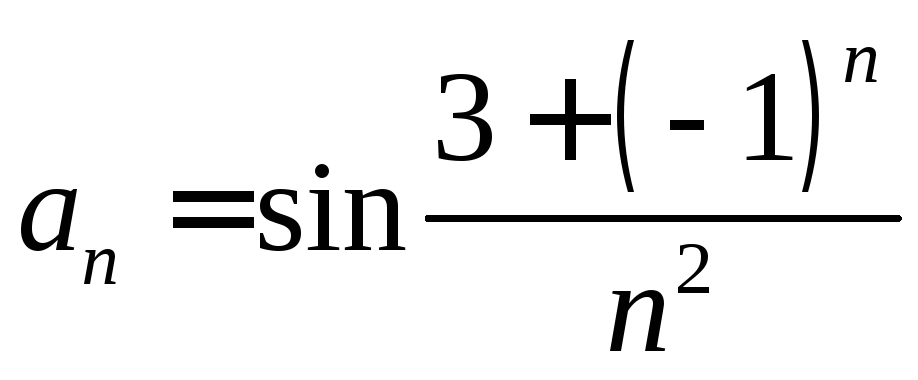 .
.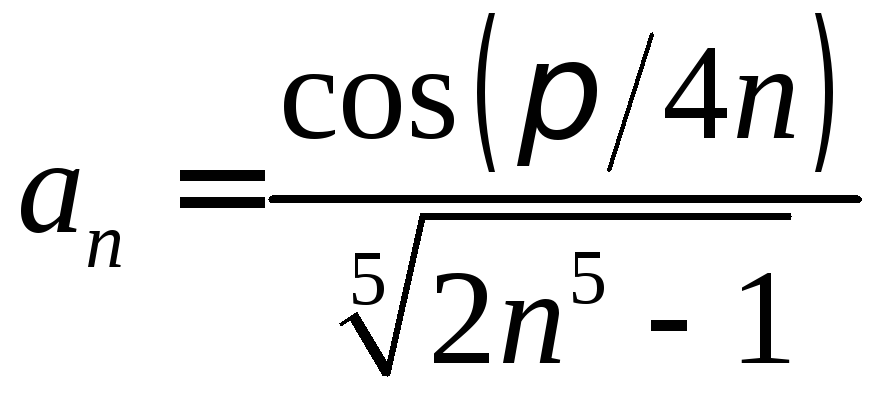 .
.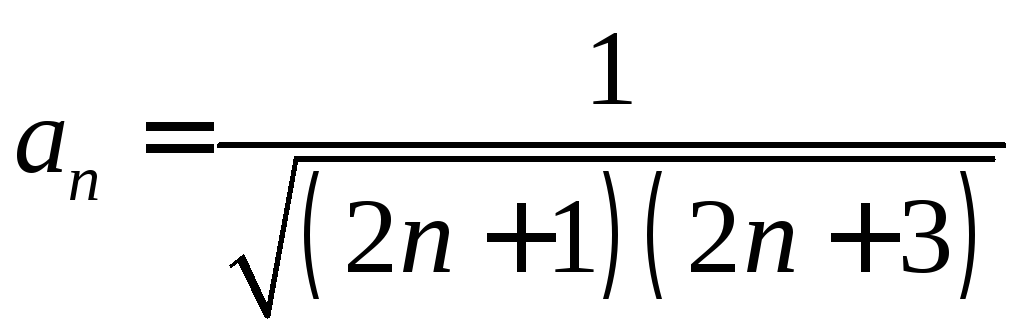 .
.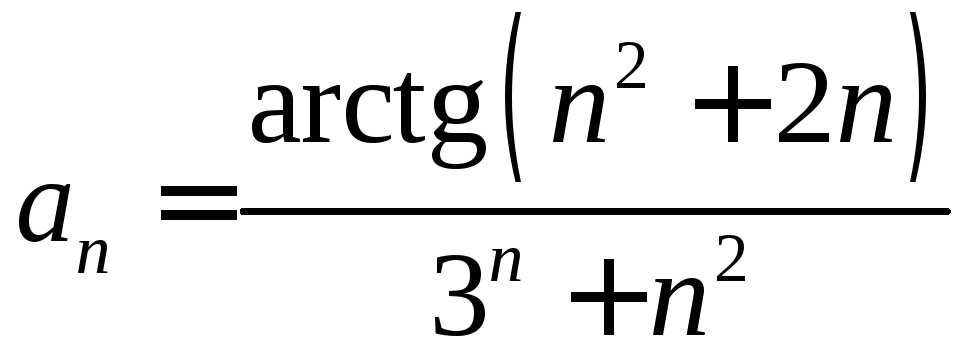 .
.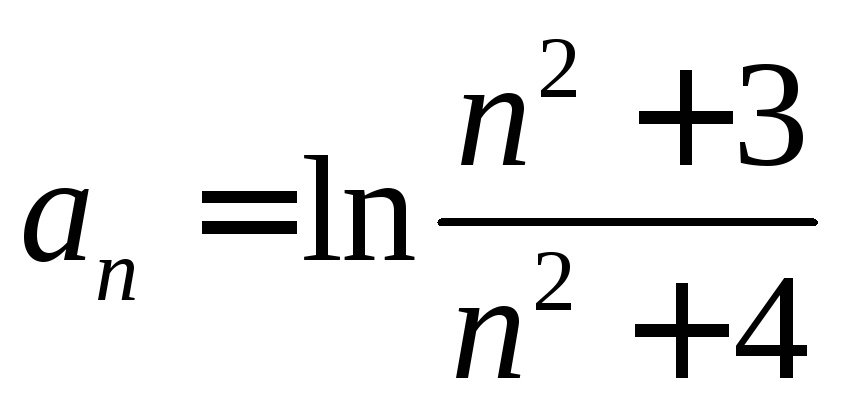 .
.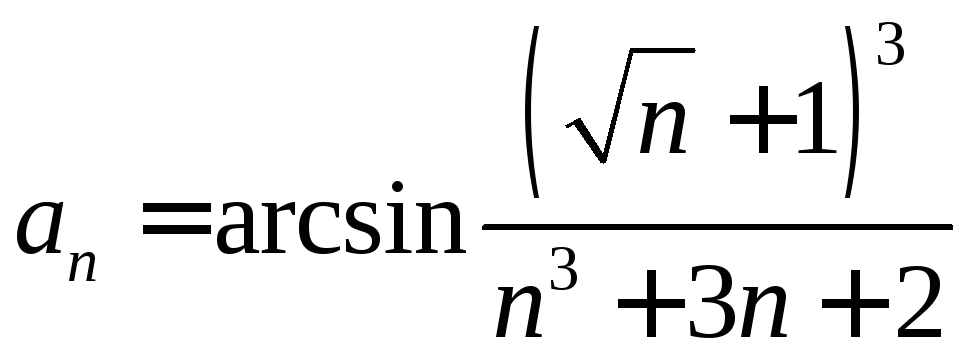 .
.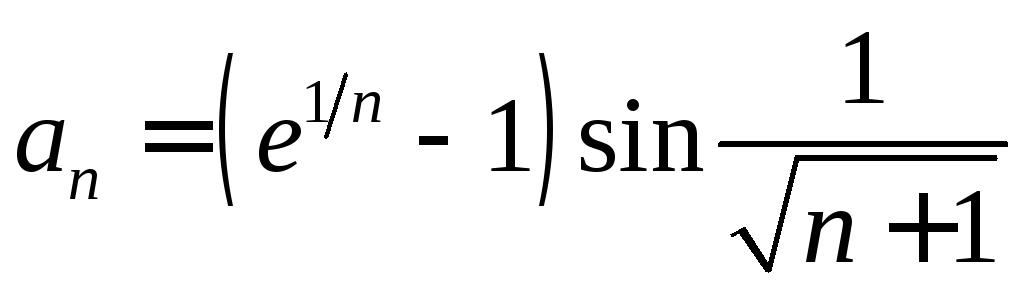 .
.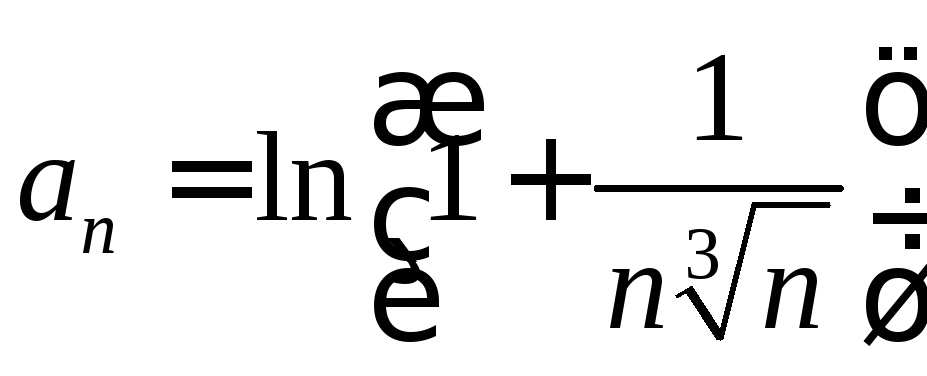 .
. .
.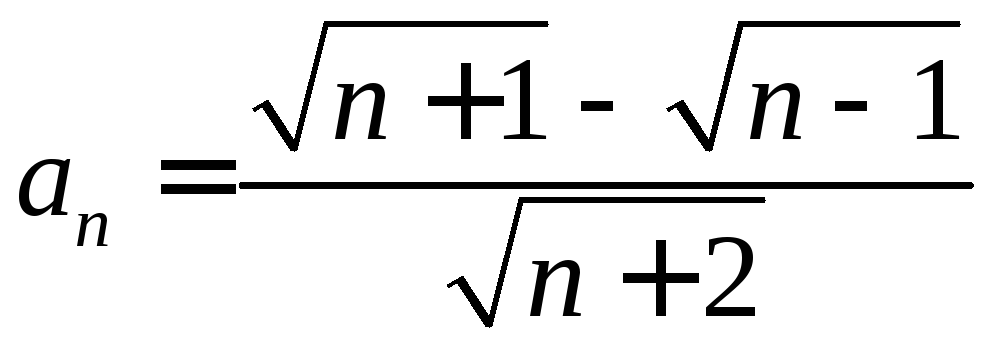 .
. .
.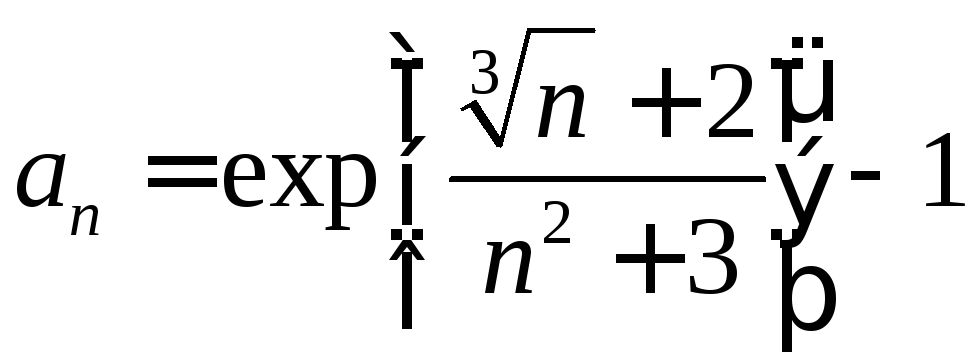 .
.