5. Криволинейное движение.

В общем случае криволинейного неравномерного движения скорость изменяется как по величине, так и по направлению. Полное ускорение, которым обладает движущаяся точка, определяет оба вида изменения скорости. Рассмотрим движение материальной точки по криволинейной плоской траектории. Вектор скорости направлен всегда по касательной к траектории. Найдем вектор изменения скорости:

,

где Δv– характеризует изменение скорости и по величине и направлению. Разложим Δvна две составляющие:

а) вектор CK– направлен по касательной от точки А и характеризует изменение скорости по величине за время Δt, в течении которого пройдена дуга АВ. CK → Δvτ–тангенциальнаясоставляющая вектора изменения скорости. б) вектор CMнаправленный в пределе (когда Δt→ 0) по радиусу к центру кривизны, характеризует изменение скорости по направлению и называетсянормальнойсоставляющей вектора изменения скорости:CM → Δvn

Тогда имеем:

Учитывая, что , имеем:

Рассматривая приближения, можно показать:

1) при 2) при 3) модуль полного ускорения определяется как: , т.к. векторы ускоренийивзаимно перпендикулярны, то Угол – определяет направление полного ускорения.

II.Законы Ньютона,их физическое содержание.

Динамика изучает состояние движения материальных тел как результат взаимодействия между ними. Основа решения динамических задач в классической механике – три закона движения, сформулированные И. Ньютоном в книге “Математические начала натуральной философии” (1689 г.). Чтобы сформулировать законы динамики введем динамические параметры движения:

а)сила– взаимодействие тел, в результате которого тела приобретают ускорение или деформируются, или имеет место и то и другое одновременно.

Следовательно о наличии сил можно судить:

1) по их динамическому проявлению (по ускорению);

2) по статическому проявлению (по деформациям);

б)масса– мера количества материи.

Для массы выполняется закон сохранения.

Масса всех взаимодействующих тел до взаимодействия равна их массе после взаимодействия.

Масса тел проявляется в двух свойствах:

1. в свойстве притягивать к себе другие тела (и притягиваться ими) – гравитация.

2. в инерции тел.

В релятивистской механике (v≈ С):

,

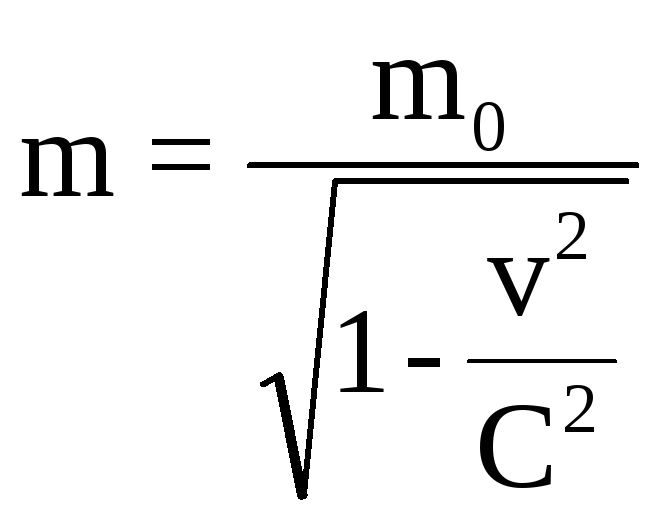где m₀– масса покоя, т.е. когдаv<<C.

Здесь нарушения закона сохранения массы нет, т.к. ускоряемая частица получает массу вместе с энергией от того поля, за счет которого растет ее скорость.

Сформулируем законы динамики для движения материальных тел.

1-й закон

Всякое тело сохраняет состояние относительного покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не изменит этого состояния.

Первый закон позволяет считать комбинацию действующих сил динамически эквивалентной их отсутствию, т.е. их сумма равна нулю. Поэтому математически закон выражается уравнением:

Согласно этому закону силы не являются первопричиной движения. И в отсутствии сил тела движутся. Это инерциальное движение тела.

Инерция

Свойство материального тела сохранять в отсутствии сил состояние покоя или равномерного и прямолинейного движения.

Инерция тел проявляется также в том, что изменение движения тела под действием сил происходит не мгновенно, а протекают во времени.

2-й закон

Тело получает ускорение пропорционально действующей на него силе и обратно пропорционально его массе. – равнодействующая

Это основной закон динамики для поступательного движения.

3-й закон

Силы, с которыми взаимодействуют тела, равны по величине и противоположны по направлению и никогда не уравновешивают друг друга, т.к. приложены к разным телам (закон действия и противодействия).

Пример:

а) тело, притягиваясь к Земле, действует на опору – вес тела б) на тело со стороны опоры, действует сила реакции . При взаимодействии тел наблюдается как прямое действие, так и действие на расстоянии.