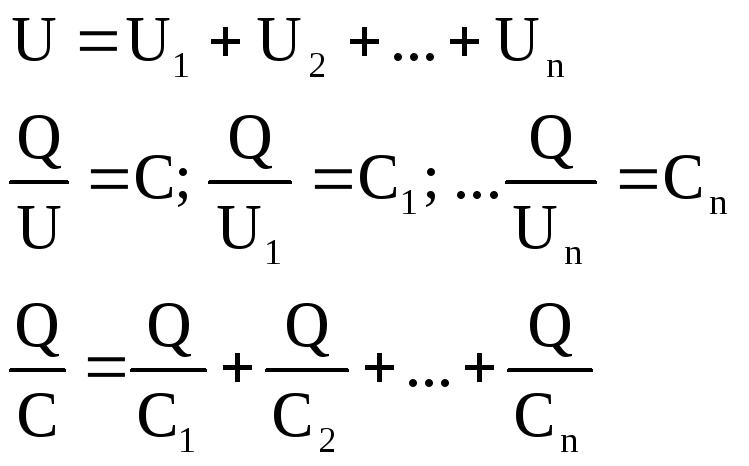- •Лекция №10. Проводники и диэлектрики в электрическом поле.
- •I.Электрическое поле вне и внутри проводника.
- •II.Распределение зарядов на поверхности проводника.Роль острия.
- •III.Электроемкость проводников.
- •IV.Конденсаторы.Вычисление емкости конденсаторов.
- •V.Энергия заряженного конденсатора.Энергия электрического поля.
- •VI.Электростатические явления в диэлектриках.
- •Опыт №1
- •VII.Поле диполя.Диполь в электрическом поле.
- •VIII.Виды диэлектриков.
- •IX.Диэлектрики во внешнем электрическом поле.
- •X.Виды диэлектриков.
III.Электроемкость проводников.
Имеется уединенный проводник. Ему сообщен заряд Q. Вычислим электрический потенциал в точке М.
|
|
Для заряда единичного:
Для заряда Q: |
Если на проводник поместить заряд Q·b, то
![]()
Потенциал в каждой точке поля возрастает прямо пропорционально заряду проводника, т.е. φ ~ Q.
![]() , (2)
, (2)
где с – электрическая ёмкость (ёмкость)
Или можно показать: ΔQ=cΔφ
![]() (3)
(3)
Физический смысл емкости.
|
Электрическая емкостьпроводника численно равна величине заряда, который нужно сообщить проводнику для увеличения его потенциала на единицу. |
Отметим, что все предыдущее справедливо, если при этом не меняются формы и размеры проводника, а также внешние условия (среда, расположение окружающих предметов).
СИ: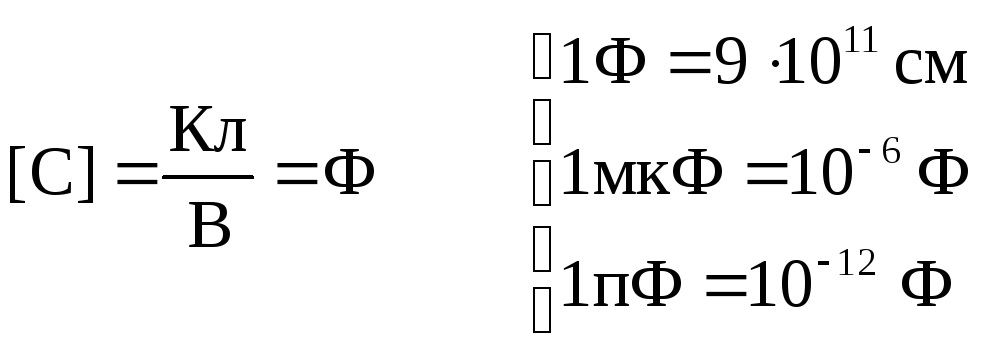
IV.Конденсаторы.Вычисление емкости конденсаторов.
Конденсаторомназывается система двух (или более) проводников, имеющих такую форму и расположение относительно друг друга, что поле, создаваемое такой системой, локализовано в ограниченной области пространства.
Примеры конденсаторов:
|
а) плоский;
|
б
|
в |
Проводники, образующие конденсатор, называются обкладками.
Чтобы зарядить конденсатор, нужно присоединить его обкладки к источнику напряжения или одну обкладку соединить с Землей, а другую («+») с клеммой источника.
|
|
Рассмотрим плоский конденсатор (или любой другой). На пластине А заряд (+Q), на пластине В по индукции заряд (–Q). Причем +Q=–Q. Поле сосредоточено между пластинами, потенциалы которых φAиφB. |
Емкостью конденсатора Сназывается величина, измеряемая отношением зарядаQна одной пластине к разности потенциалов между пластинами:
![]() (4)
(4)
Примеры вычисления емкости конденсаторов.
1. Плоский конденсатор.
|
|
d<<S, тогда, согласно теоремы
Остроградского-Гаусса, поле между
пластинами: С другой стороны:
|
![]()
![]()
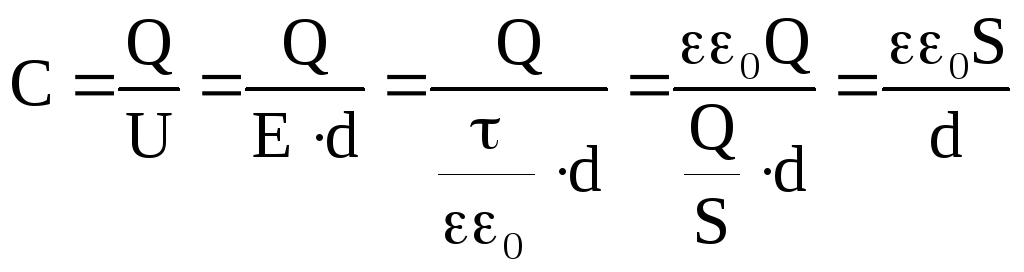
![]() (5)
(5)
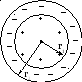
2. Сферический конденсатор.
|
|
|
Положим: r1–r2=d;d<<r1, тогдаr1≈r2≈r
Следствие: ![]() если зазор мал, то Спл= Ссф
если зазор мал, то Спл= Ссф
если r1>>r2, то Ссф= 4πεε0r→Cсф= Сшара
3. Цилиндрический конденсатор.
![]() (7)
(7)
Если напряжение Uна конденсаторе сделать слишком большим, то происходит разряд через слой диэлектрика – пробой. Поэтому каждый конденсатор характеризуется не только своей емкостью С, но и максимальным рабочим напряжениемUmax=Uпр.
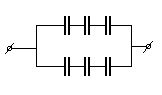
Располагая разными по ёмкости конденсаторами, можно получить желаемую емкость, путем соединения конденсаторов:
|
а) последовательное:
|
б |
в) смешенное
| |
|
|
Q = Q1 + Q2 + … + Qn UC = Q CU = C1U + C2U + … +CnU C = C1 + C2 + … +Cn
| ||
V.Энергия заряженного конденсатора.Энергия электрического поля.
Для многих вопросов теории и практики необходимо определять электрическую энергию заряженного проводника. (Определяем через работу разряда проводника).
Пусть имеется проводник с зарядом Qи начальным потенциалом φ0. Тогда элементарная работа при переходе элементарного зарядаdQс проводника на землю равна:
dA=φ·dQ, где
– мгновенное значение потенциала, но
dQ= –Cdφ(“–“ – означает уменьшение потенциала).
dA = –Cφ·dφ
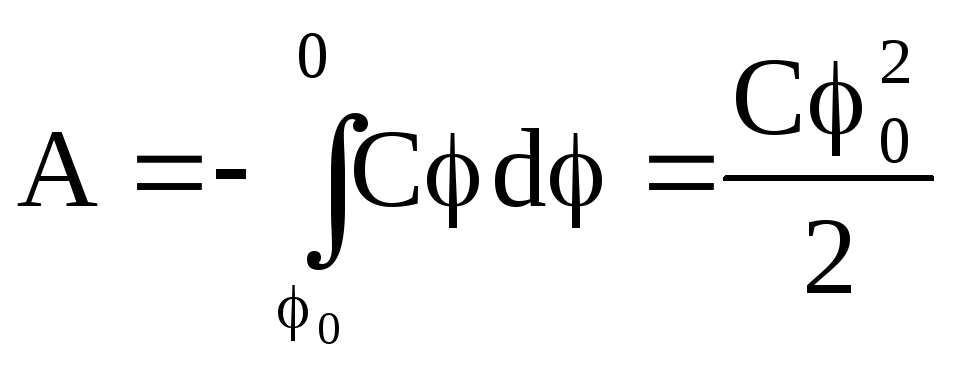
Найденная работа совершилась за счет убыли потенциальной энергии и численно равна энергии заряженного проводника W:
![]()
|
Энергия заряженного
конденсатора:
|
Формула для энергии заряженного тела по существу определяет и энергию электрического поля созданного заряженным телом:
![]() (8)
(8)
Объемная плотность энергииэлектростатического поля – физическая величина, численно равная отношению потенциальной энергии поля в единице объема.
![]()
![]() (9)
(9)
![]()

 )
шаровой:
)
шаровой: )
цилиндрический
)
цилиндрический

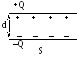
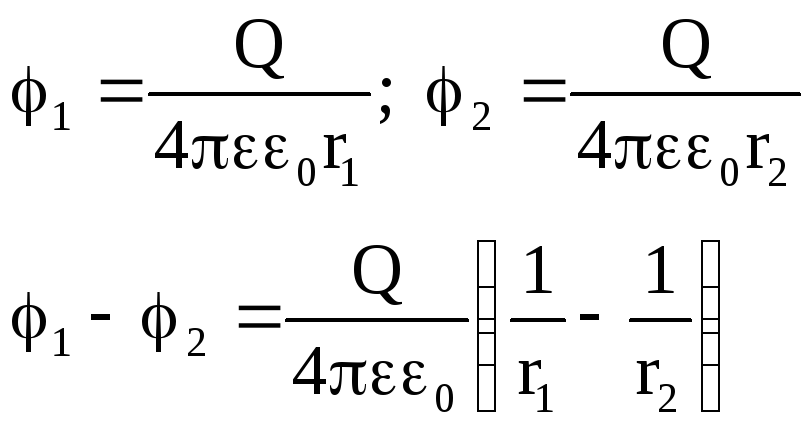
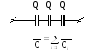
 )
параллельное:
)
параллельное: