
Учебники / 0841558_16EA1_federico_milano_power_system_modelling_and_scripting
.pdf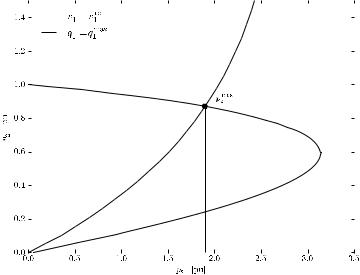
5.2 System Model |
107 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 5.3 PV curve for the 2-bus system considering generator reactive power limits
5.2System Model
In order to generalize the concepts presented in the previous section, it is necessary to define a power system model suitable for encountering the maximum loading condition. With this aim, the power flow model is modified as follows:
0 = g(y, μ) |
(5.10) |
where y are, as usual, the algebraic variables and μ R is a loading parameter, i.e., a scalar independent parameter that multiplies all generator and load powers, as follows:
pG = (μInG + kGΓ )pG0 |
(5.11) |
pL = μpL0 qL = μqL0
where InG is the identity matrix of order nG, Γ = diag(γ1, γ2, . . . , γnG ) are generator loss participation factors, kG is a scalar variable used for accomplishing the distributed slack bus model as discussed in Subsection 4.4.9 of Chapter 4, and pG0, pL0 and qL0 are the “base case” or initial generator and load powers, respectively.
108 |
5 Continuation Power Flow Analysis |
An alternative loading model that can be found in the literature is:
pG = (InG + μ˜InG + kGΓ )pG0 |
(5.12) |
pL = (1 + μ˜)pL0 qL = (1 + μ˜)qL0
where μ˜ expresses the distance of the base case to the stressed operating condition and μ˜max is thus the distance to the point of collapse.
Another loading model is as follows:
pG = pG0 + (μ˘InG + kGΓ )pS0 |
(5.13) |
pL = pL0 + μ˘pD0 pL = pL0 + μ˘pD0
where pS0, pD0 and qD0 are called generator (or supply) and load (or demand) power directions since they define a custom path along which the system is loaded through the parameter μ˘. The three models (5.11), (5.12) and (5.13) are equivalent and do not introduce conceptual di erences. Thus, in the following, unless explicitly stated, model (5.11) is used.
5.3Direct Methods
Probably, the most intuitive approach for solving the maximum loading condition problem is to use a direct method. The idea is to encounter a set of equations that defines the point of collapse of the power system modelled as (5.10). As observed in Section 5.1, system equations change depending on the type of maximum loading condition: transmission system or reactive power limit. Thus one has to formulate a di erent set of equations for each type of maximum loading condition.
In the literature, this task has been assessed with the help of bifurcation theory which allows defining a taxonomy of the points of collapse, which are, in turns, bifurcation points. A bifurcation point is a solution of (5.10) that satisfies certain mathematical conditions. In particular, classical power flow equations can show only two kinds of bifurcation points, namely, the saddle-node bifurcation and limit-induced bifurcation.
It is important to note that bifurcation theory applies to dynamical systems (i.e., ordinary di erential equations), while the power flow equations (5.10) are algebraic. Thus, strictly speaking, stability concepts and bifurcation theory cannot be applied to (5.10). However, it is common practice to associate the maximum loading condition with bifurcation points and, hence, to infer the static voltage stability region of the power system through the analysis of algebraic power flow equations.
5.3 Direct Methods |
109 |
Using stability concepts proper of dynamical systems for a set of algebraic equations can be justified in mathematical terms if one considers that (5.10) can be rewritten as:
T y˙ = g(y, μ(t)) |
(5.14) |
where T = diag(T 1, T 2, . . . , Tny ) is a diagonal matrix composed of “small” time constants. Furthermore, the time dependent variation of μ(t) is assumed to be “slow”, so that system dynamics are considered steady-state and systems devices are approximated by means of the models used in the classical power flow analysis. These assumptions agree with the definition of algebraic variables given in Section 1.4 of Chapter 1. Further insights on (5.14) are given in Section 8.6 of Chapter 8.
5.3.1Saddle-Node Bifurcation
The Saddle-Node Bifurcation (SNB) is the formal mathematical notation of the transmission system limit that is described in Section 5.1. Figure 5.2 shows that the tangent to the curve v2(p2) at the maximum loading point is vertical, i.e., dv2/dp2 → ∞ at the point of collapse.
The conditions for a SNB point are as follows:
g(y, μ) = 0 |
(5.15) |
gy ν = 0
ν 2 = 1
or
g(y, μ) = 0 |
(5.16) |
gTy w = 0
w 2 = 1
where v and w are the right and the left eigenvectors, respectively, and the operator ·2 indicates the Euclidean norm. The solution of (5.15) and (5.16) can be obtained by means of a Newton’s method, which requires to compute and factorize the Jacobian matrix. For example, the complete Jacobian matrix of (5.15) is:
gy |
0 |
gμ |
|
(5.17) |
gyy ν |
gy |
0 |
||
|
|
|
|
|
0∂ ν 2/∂ν 0
The Euclidean norm |ν| reduces the sparsity of the Jacobian matrix computed at each iteration of the Newton’s method, but allows avoiding refactorizations (as happens in the case of ∞-norm) and is numerically more stable than the 1-norm. Since (5.17) requires the calculations of the Hessian

110 |
5 Continuation Power Flow Analysis |
matrix gyy , direct methods are computationally expensive. Furthermore, if the number of buses is nb, the variables in (5.15) or (5.16) are 2nb + 1.
Unfortunately, even assuming that modern computers and adequate functions for handling sparse matrices are able to reduce the computational burden, problems (5.15) and (5.16) are hard to solve. The main issue is to find a good initial guess for the eigenvectors ν or w. This is not an easy task since the eigenvector elements vary drastically close to the bifurcation point. Thus, in order to find a good initial guess, one has to start relatively close to the bifurcation point.
Example 5.1 Saddle-Node Bifurcation of the 2-Bus System
This example provides the analytical expression of the SNB point of the 2- bus system of Figure 5.1. System data are: v1ref = 1 pu, xL = 0.1 pu, and cos φ2 = 0.9 lag. Due to the simplicity of the problem, the solution can be find analytically. The value of pmax2 is:
|
|
(vref )2 |
|
|
|
|
|
p2 |
= |
(− tan φ2 + 1 + tan2 φ2) = 3.1339 pu |
(5.18) |
||||
2xL |
|||||||
max |
1 |
|
|
|
|
||
Equation (5.18) can be obtained by imposing that the argument of the inner square root of (5.4) is zero:
(p2max tan φ2xL − (v1ref )2/2)2 − xL2 (p2max)2(1 + tan2 φ2) = 0 |
(5.19) |
And, substituting (5.18) in (5.4), one obtains:
v2 = √−a = |
|
|
|
(5.20) |
||
2 |
− p2 tan φ2xL = 0.5901 pu |
|||||
M |
|
|
(vref )2 |
|
|
|
|
|
1 |
max |
|
||
The same solution can be found observing that the second equation of (5.16) implies that the Jacobian matrix gy has to be singular at the SNB point.1 This is another way of imposing the the tangent of v2(p2) is vertical at the SNB. Since in this simple case the power flow Jacobian matrix size is 2 × 2, one can compute analytically the determinant. The Jacobian matrix of (5.1) is:
gy = |
1 |
|
v1ref v2 cos θ2 |
v1ref sin θ2 |
|
(5.21) |
||
x |
ref |
v2 sin θ2 |
ref |
cos θ2 |
||||
|
L |
v1 |
2v2 − v1 |
|
|
|||
Hence, imposing that the determinant is zero leads to:
2 |
vref v2 |
cos θ2 − |
vref v2 |
= 0 |
(5.22) |
1 |
1 |
||||
xL |
xL |
1 In fact ν cannot be zero because of the constraint ν 2 = 1.

5.3 Direct Methods |
111 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 5.4 Graphical illustration of the direct method for computing the SNB of the 2-bus system
The trigonometric function cos θ2 can be substituted for the expression deduced by the second of (5.1):
|
1 |
|
|
(5.23) |
|
cos θ2 |
= |
|
|
v2 + xLp2 tan φ2 |
|
|
|
||||
|
|
v1ref v2 |
|
||
|
|
|
2 |
|
|
Thus (5.22) and (5.23) lead to: |
|
|
|
||
|
p2 = |
(v1ref )2 − 2v22 |
(5.24) |
||
|
2xL tan φ2 |
||||
|
|
|
|
||
The intersection of (5.6) and (5.24) is the SNB point (see Figure 5.4).
5.3.2Limit-Induced Bifurcation
Limit-Induced Bifurcations (LIBs) allow formally defining maximum loading conditions due to generator reactive power limits. LIB points are the solution of two sets of equations:
0 = g1(y, μ) |
(5.25) |
0 = g2(y, μ) |
|

112 |
5 Continuation Power Flow Analysis |
where g1 and g2 di er in the model of some devices. For example, let us assume that in g1 a certain generator is modelled as a constant pv and that in g2 the same generator is modelled as a constant pq, with q = qmax. Then, the LIB point is the intersection of the two sets of power flow equations g1
and g2.
In practice, it is not necessary to duplicate all equations, since at the LIB point (y, μ) is the same for the two systems. It su ces to solve:
0 = g(y, μ) |
(5.26) |
0 = g˘(y, μ)
where g ≡ g1 and g˘ ≡ g2 is a scalar equation that imposes the desired additional constraint. For example, assuming that the limit is a generator reactive power, g can model the generator at bus h as a constant pv and g˘ is:
g˘ = qGh − qGhmax |
(5.27) |
In principle, one can impose more than one scalar constraint in (5.26). As a matter of fact, not all LIBs lead to the maximum loading condition (see Example 5.4). Moreover, constraints can be of any kind, e.g., voltage limits, transmission line thermal limits, etc. However, in the literature, LIBs generally concern only generator reactive power limits, since only these limits can lead to a point of collapse.
In mathematical terms, a LIB is not characterized by a Jacobian matrix singularity. The Jacobian matrix is only discontinuous at the bifurcation point. This property is used in continuation power flow analysis for distinguishing between SNB and LIB points.
Example 5.2 Limit-Induced Bifurcation of the 2-Bus System
For the 2-bus example of Figure 5.1, the LIB point can be determined analytically. In particular, the intersection of (5.6) and (5.9) can be determined solving the following system:
|
|
|
v vref |
|
|
|
|
|
|
|
|
|
||
− p2 |
= |
2 |
1 |
|
sin θ2 |
|
|
|
(5.28) |
|||||
|
xL |
|
|
|
|
|||||||||
|
= |
v2 |
|
|
v2vref |
cos θ2 |
(5.29) |
|||||||
−q2 |
2 |
− |
|
|
|
1 |
||||||||
xL |
|
|
xL |
|||||||||||
max |
= |
(vref )2 |
|
v2vref |
cos(−θ2) |
(5.30) |
||||||||
1 |
|
|
|
− |
|
|
1 |
|||||||
q1 |
|
|
|
|
|
|
|
|||||||
|
xL |
|
|
|
xL |
|||||||||
From (5.30) and (5.29): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
2 |
= |
(v1ref )2 − v22 |
− |
qmax |
(5.31) |
||||||||
|
|
|
|
|
xL |
|
|
|
1 |
|
||||

5.3Direct Methods
Then, substituting (5.31) in (5.2), one obtains:
(b − 1)v24 + dv22 + dc2 = 0
where:
b = 1 + tan2 φ2 tan2 φ2
c = xLq1max − (v1ref )2
d = (1 − 2b)(v1ref )2 + 2xL(b − 1)q1max
The only physical solution of the bi-quadratic equation (5.32) is:
v2M = |
|
|
|
|
|
|
|
|
|
= 0.8708 pu |
|
|
− − |
2(b− |
|
1) |
− |
|
|
||||
|
|
|
d |
|
− |
|
|
1)c2 |
|
||
|
|
|
|
d2 |
4b(b |
|
|||||
113
(5.32)
(5.33)
(5.34)
Finally, pmax2 = p2(v2M ) can be determined indi erently from (5.6) or (5.9), that yield pmax2 = 1.8928 pu. These results are obtained assuming the following system data: q1max = 1.5 pu, xL = 0.1 pu, and cos φ2 = 0.9 lag.
5.3.3Nonlinear Programming
Another class of direct approaches consists in formulating the maximum loading condition as a nonlinear programming problem. This approach has proved to be robust [35, 36, 37, 259]. Furthermore, the formulation as an optimization problem allows including a variety of constraints and setting up complex models [198, 260]. Due to the relevance of nonlinear programming in power system analysis, the entire Chapter 6 is dedicated to this topic. This section only provides a simple yet relevant example.
Example 5.3 Optimization Problem Equivalent to the Saddle-Node Direct Method
This example proves that (5.16) is formally equivalent to an optimization problem. This proof firstly appeared in [36]. Consider the following problem:
Minimize |
−μ |
(5.35) |
y, μ |
|
|
subject to |
g(y, μ) = 0 |
|
The Lagrangian function associated with problem (5.35) is:
L (y, μ, ρ) = −μ + gT (y, μ)ρ |
(5.36) |
114 5 Continuation Power Flow Analysis
whose the Karush-Kuhn-Tucker’s optimality conditions are: |
|
g(y, μ) = 0 |
(5.37) |
gyT ρ = 0 |
|
gT ρ = 1 |
|
μ |
|
Thus, the global minimizer of (5.35) is a solution of (5.16). In fact, the left eigenvector is equal to the vector of dual variables (w = ρ) and the condition gTμ ρ = 1 is equivalent to w 2 = 1 since its e ect is to impose that the vector of dual variables is not zero (ρ = 0).
The analogy between direct methods and nonlinear programming problems can be extended to LIBs given that proper inequalities and complementarity constraints are included in (5.35). The interested reader can find a rigorous proof in [21].
5.4 Homotopy Methods
The common feature of all direct methods is to find a single solution, i.e., the maximum loading condition. Since the objective is to find the maximum loading condition, one may argue that direct methods provide just the required information. Actually, this is not completely true. The nose curves shown in Figures 5.2 and 5.3 provide much more information than the mere bifurcation point (v2M , pmax2 ). In fact, nose curves provide a continuous set of solutions, one of which is the maximum loading condition. This continuous set allows understanding the behavior of the system likely better than the single bifurcation point. Moreover, important drawbacks of the direct methods discussed above except for the nonlinear programming approach are:
1.The solution can be di cult to obtain as a good initial guess is required. This is especially true for determining SNB points.
2.Each bifurcation point is treated separately. Since one does not know a priori whether a LIB or a SNB yields the maximum loading condition, taking into account all possible bifurcations (a real-world system can show tens of LIBs before getting to the maximum loading condition) can be a lengthy process.
Finally, with regard to the nonlinear programming approach, it has to be noted that the computational burden of an optimal power flow problem of a real-size system is not negligible.
To overcome the drawbacks of direct methods, consider the following strategy. Starting from an initial solution (e.g., base case) of (5.10), the loading parameter μ is increased by a small amount, say Δμ, and then (5.10) is solved again for the new value μ + Δμ. The operation is repeated as long as the solution of (5.10) cannot be found. This procedure is known as embedding algorithm [147]. In case (5.10) represent power flow equations, this procedure
5.4 Homotopy Methods |
115 |
yields a series of power flow solutions, of which the last one is supposedly the maximum loading condition.
The critical point of the embedding algorithm is the word supposedly. In fact, there is no guarantee that the procedure ends at the maximum loading condition. Each solution is obtained by means of an iterative algorithm (e.g., Newton’s method) and thus failing to obtain the convergence can be due either to numerical issues or to the fact that the solution actually does not exists. This issue is unsolvable, even using some robust technique as those described in Chapter 4. Other critical issues of the embedding algorithm are:
1.At SNB points, the Jacobian matrix is singular. Thus the Newton’s method surely diverges for cases close enough to SNB points.
2.The number of steps and the magnitude of Δμ are not known a priori. In any case, Δμ has to be su ciently small to ensure that the Newton’s method applied to the next step converges. This fact prevents from using parallel computing as the initial guess of each step is the solution of the previous step. Thus, the computational burden of embedding algorithms is generally high.
A solution to all issues above is provided by homotopy methods [218]. The homotopy approach consists in defining a homotopy map ψ based on the original system equations g(y), as follows:
ψ(y, μ) = g(y, μ) |
(5.38) |
where the main di erence between g and ψ is that in the latter μ is a variable of the system, thus g : Rny → Rny and ψ : Rny +1 → Rny . According to the definitions given in Section 1.4 of Chapter 1, μ (μ R) is an independent variable (i.e., μ = [μ]) and ψ : Rny ×Rnμ → Rny where nμ = 1. In homotopy methods, μ is called continuation parameter. However, in the following, μ is called loading level, thus referring to its physical meaning rather to the mathematical one.
Equation (5.38) may seem trivial since ψ and g coincide. This is because (5.38) is a forced or natural parameter homotopy, i.e., μ is a parameter of g. It is important to note that, in general, homotopy maps can be defined also using an external parameter that has no physical meaning and no relation with g(y). In this case, the homotopy is called free-running or artificial parameter homotopy and has the general form:
ψ(y, μ) = (1 − μ)r(y) + μg(y) |
(5.39) |
where μ [0, 1] and r(y) is an arbitrary smooth function. However, in the following, only forced homotopy methods are considered.
Parametrizing y and μ by means of an arc length s, one has:
ψ(y(s), μ(s)) = 0 |
(5.40) |
116 |
5 Continuation Power Flow Analysis |
and di erentiating (5.40) with respect to s:
|
|
dψ |
|
|
|
ψy |
dy |
|
|
|||
|
|
= |
ds |
(5.41) |
||||||||
|
|
|
|
|||||||||
|
|
|
ds |
|
ψμ dμ |
|
|
|||||
|
|
|
|
|
|
|
|
|
ds |
|
|
|
with: |
|
|
|
|
|
|
|
|
|
|
|
|
ds , |
ds |
2 |
= 1 |
(5.42) |
||||||||
|
|
|
dy |
dμ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
and initial conditions: |
|
|
|
|
|
|
|
|
|
|
||
|
y(0) = y(0), |
|
μ(0) = μ(0) |
(5.43) |
||||||||
Equation (5.41) is used for mapping ψ along a path parametrized by s. For a current point (y(i), μ(i)), the next point (y(i+1), μ(i+1)) can be found using a predictor-corrector method. In particular, the predictor step can be as follows:
y˜(i+1) |
= y(i) + y(i) = y(i) + k |
dy |
(5.44) |
|||
ds |
||||||
|
|
|
|
|||
μ˜(i+1) |
= μ(i) + Δμ(i) = μ(i) + k |
dμ |
|
|
||
|
|
|||||
|
|
|
ds |
|
||
where k is an adequate step size. The corrector step consists in ensuring that the point (y(i+1), μ(i+1)) satisfies the condition ψ(y(i+1), μ(i+1)) = 0. A possible choice of the corrector step is to solve an optimization problem, as follows:
Minimize |
(y(i+1) − y˜(i+1), μ(i+1) − μ˜(i+1)) 2 |
(5.45) |
y, μ |
|
|
subject to |
ψ(y(i+1), μ(i+1)) = 0 |
|
Although elegant, the solution of (5.45) for each step of the path can be cumbersome. In practical applications, it is thus preferred to substitute the optimization problem (5.45) for:
g(y, μ) = 0 |
(5.46) |
(y, μ, y˜(i+1), μ˜(i+1)) = 0
where : Rny +1 → R is the continuation function. How to choose depends on the application. Subsection 5.4.3 discusses typical expressions of used in the continuation power flow analysis.
The mathematical construction above may appear artificial. However, the advantage of homotopy methods is the robustness. The convergence is guaranteed by a series of theorems that the interested reader can find in [218]. Moreover, the homotopy approach has been successfully applied to
