
Учебники / 0841558_16EA1_federico_milano_power_system_modelling_and_scripting
.pdf
3.5 Python Scripting Language |
55 |
filters.read(), one should be sure that input format, datafile, path, and addfile are enough information for any current and future parser. Since one cannot anticipate the future, this is clearly impossible. For example, if a specific data format requires two additional files, the argument list above is incomplete. Fortunately, thanks to the possibilities o ered by modern scripting languages such as Python, it is sometime possible to anticipate the future or, in other words, to make that future changes do not a ect the current structure of the program. In this case, the ability of introspection can be useful. If addfile is a list of strings rather than a simple string, one can define any number of additional data files. The only di erence in the code is that the wrapper filters.read() has to check the type of addfile. This is easily done by:
if type(addfile) == list:
some action
else:
some other action
The built-in Python function type is a simple way of implementing introspection.
Device Interface Class
The class function described in Script 3.1 is a quite simple solution to the problem of interfacing the solver with function types. The class function calls all functions defined in the list flist, no matter if calling these functions is required or not. If the number of elements is small, there is no real e ciency issue and the class function does not need to be optimized.
Unfortunately, for a power system software package, the number of possible devices can be huge. In EPRI Extended Transient-Midterm Stability Program manual [130], tens of AVRs, turbine governors and PSS devices are defined. Furthermore, scripting-based tools for power system analysis are the ideal platform on which building user-defined models.
The key point is that most of these models are likely never used together in the same network. Thus, there is a potential disproportion between the devices normally used and the ones that are actually defined in the package. For example, say that the defined devices are 100 and that those required in a simple benchmark system are 10. During a time domain analysis, device methods are called thousands of times. It is clearly ine cient to call all 100 device methods since 90% of them actually does nothing.
This problem is not new. For example, PSCAD [183] faces a similar issue for solving electro-magnetic transients. However, the solution is strongly dependent on the programming language used. In PSCAD, mathematical routines are written in FORTRAN which is a system language. The only solution in this case is to create for each case study a specific routine and compiling it with a FORTRAN compiler. Thus, in the case of PSCAD, the interface actually collects the information of the system topology and devices

56 |
3 Power System Scripting |
and writes the equations of the system in form of FORTRAN code. The results is certainly e cient since the program that is executed is specifically suited for the case study. However, one has to write and compile a certain amount of code before running the simulation.
Scripting languages allows implementing the approach discussed above, but also provide other interesting solutions. One of these solutions relies on meta-programming. The key point is that a scripting language is interpreted and not compiled. Thus, a script can be used for generating code fragments during its execution and then for executing that code “on the fly”. This feature can be conveniently used for implementing the interface class.
For example, suppose that we want to solve a numerical integration for the IEEE 14-bus system. Assuming that an implicit solver is used, one has to call, at each iteration of each time step (see also Chapter 8 for mathematical details on implicit numerical methods) the di erential and algebraic equations as well as Jacobian matrices of di erential and algebraic equations.
The following code implements the concept of meta-programming previously discussed.
import system
class device:
self.n = 0 self.gcall = [] self.gycall = [] self.fcall = [] self.fxcall = []
def init (self, device list):
self.devices = device list
def setup(self):
self.n = 0
for item in self.devices:
if system. dict [item].n: self.n += 1 self.devices.append(item)
properties = system. dict [item].properties for key in properties.keys():
self. dict [key].append(properties[key])
string = ’"""\n’
for gcall, device in zip(self.gcall, self.devices):
if gcall: string += ’system.’ + device + ’.gcall(system.DAE)\n’ string += ’\n’
for gycall, device in zip(self.gycall, self.devices):
if gycall: string += ’system.’ + device + ’.gycall(system.DAE)\n’ string += ’\n’
for fcall, device in zip(self.fcall, self.devices):

3.5 Python Scripting Language |
57 |
||
if |
fcall: |
string += ’system.’ + device + ’.fcall(system.DAE)\n’ |
|
string |
+= ’\n’ |
|
|
for fxcall, device in zip(self.fxcall, self.devices): |
|||
if |
fxcall: |
string += ’system.’ + device + ’.fxcall(system.DAE)\n’ |
|
string |
+= ’"""’ |
|
|
self.call int = compile(eval(string), |
’’, ’exec’) |
||
The first part of the method setup scans all devices defined in the structure system. This operation is quite simple in Python thanks to the built-in dictionary dict that contains the names of all attributes of the structure. If a device is currently defined (i.e., if system. dict [item].n is a positive integer), then that device is added to the list devices. Furthermore, it assumed that each device has an attribute called properties that is a dictionary of the form:
self.properties = {’gcall’:True, ’fcall’:False, ’gycall’:True, ’fxcall’:False}
In other words, the dictionary properties specifies if a device has to be called when computing algebraic equations g (gcall), di erential equations f (fcall), algebraic Jacobian matrix gy (gycall) and remaining Jacobian matrices f x, f y and gx (fxcall).5 The class device stores the information contained in the attribute properties of each device required in the current case study.
The second part of the method setup is a meta-code that creates another code and pre-compiles it using the built-in function compile. For example, for the IEEE 14-bus system, the variable string assumes the following value:
"""
system.Line.gcall(system.DAE)
system.PQ.gcall(system.DAE)
system.Shunt.gcall(system.DAE)
system.PV.gcall(system.DAE)
system.SW.gcall(system.DAE)
system.Syn5a.gcall(system.DAE)
system.Syn6a.gcall(system.DAE)
system.Avr1.gcall(system.DAE)
system.Line.gycall(system.DAE)
system.PQ.gycall(system.DAE)
system.Shunt.gycall(system.DAE)
system.PV.gycall(system.DAE)
system.SW.gycall(system.DAE)
system.Syn5a.gycall(system.DAE)
system.Syn6a.gycall(system.DAE)
system.Avr1.gycall(system.DAE)
system.Syn5a.fcall(system.DAE)
system.Syn6a.fcall(system.DAE)
system.Avr1.fcall(system.DAE)
5 Chapter 9 provides further details on device methods and attributes.
58 |
3 Power System Scripting |
system.Syn5a.fxcall(system.DAE)
system.Syn6a.fxcall(system.DAE)
system.Avr1.fxcall(system.DAE)
"""
All devices defined in the data file (see also Chapter 21) are called depending if it contains algebraic an/or di erential equations. For example, the Shunt device is purely algebraic and is called only for computing g and gy . Each device call accepts as argument the class system.DAE that is assumed to contain the value of the complete set of di erential-algebraic equations as well as Jacobian matrices.
Part II
Power System Analysis

Chapter 4
Power Flow Analysis
This chapter describes the power flow1 analysis from both analytic and algorithmic viewpoints. Section 4.1 introduces the power flow problem through a simple example and clarifies the di erences between power flow and circuit analysis. Section 4.2 provides a taxonomy of the power flow problem, while Section 4.3 presents the standard power flow equations. Section 4.4 describes the most common algorithms used for solving this problem. These are the Gauss-Seidel’s method, the Newton’s method and its variants, the fast decoupled power flow and the dc power flow. A discussion about the single and distributed slack bus models and a comparative example are also included in Section 4.4. Section 4.5 provides a general mathematical framework for the power flow problem based on the continuous Newton’s method. Finally, Section 4.6 summarizes the most relevant concepts provided in this chapter.
4.1Background
A classical problem of circuit theory is to find all branch currents and all node voltages of an assigned circuit. Typical input data are generator voltages as well as the impedances of all branches. If all impedances are constant, the resulting set of equations that describe the circuit is linear.
For example, Figure 4.1 represents a single-phase steady-state ac system. Let us assume that the circuit shown in Figure 4.1 represents the single-phase equivalent of a symmetrical balanced three-phase transmission system where the branches between nodes 1, 2 and 3 are transmission lines, the impedance
¯ |
¯ |
are generators. |
z¯3 is a load and the independent current sources i1 |
and i2 |
Assuming node 0 as the reference voltage, the current injections at nodes 1,
1In several papers and books, especially old ones, the power flow analysis is called load flow analysis. This notation should be avoided since, quoting Concordia and Tinney [335]: “Load does not flow, but power flows.”
F. Milano: Power System Modelling and Scripting, Power Systems, pp. 61–101. springerlink.com c Springer-Verlag Berlin Heidelberg 2010

62 |
|
|
|
4 Power Flow Analysis |
|
¯ |
|
|
¯ |
|
i1 |
|
|
i2 |
|
1 |
|
|
2 |
|
|
|
jx12 |
|
|
|
jx13 |
|
jx23 |
+ |
|
|
|
+ |
v¯1 |
|
|
3 |
v¯2 |
|
|
|
||
− |
+ |
|
|
− |
|
|
|
||
|
v¯ |
z¯ |
|
¯ |
|
3 |
3 |
|
i3 |
−
0
Fig. 4.1 Classical circuit problem
2 and 3 are obtained based on the well-known branch current method 2 as the solution of a simple set of linear equations:
|
|
0 = |
v¯1 − v¯2 |
+ |
v¯1 − v¯3 |
− |
¯i |
(4.1) |
|
|
|
|
jx12 |
jx13 |
1 |
|
|||
|
|
0 = |
v¯2 − v¯1 |
+ |
v¯2 − v¯3 |
− |
¯i |
|
|
|
|
|
jx12 |
jx23 |
2 |
|
|||
|
|
0 = |
v¯3 − v¯1 |
+ |
v¯3 − v¯2 |
− |
¯i |
|
|
|
|
|
jx13 |
jx23 |
3 |
|
|||
¯ |
¯ |
|
|
|
|
|
|
¯ |
depends on the voltage |
where i1 |
and i2 |
are imposed by the generators and i3 |
|||||||
v¯3, as follows: |
|
¯ |
|
|
/z¯3 |
|
|
(4.2) |
|
|
|
|
|
|
|
|
|||
|
|
|
i3 = −v¯3 |
|
|
||||
Rewriting (4.1) and (4.2) in vectorial form, one has:
|
|
¯ |
|
|
0 |
v¯2 |
= Y¯ totv¯ |
|
(4.3) |
|
|
|
¯i2 = Y¯ + I3 |
|
|||||||
|
|
i1 |
|
|
0 |
|
v¯1 |
|
|
|
|
|
0 |
|
1/z¯3 v¯3 |
|
|
||||
|
|
|
|
|
|
¯ |
|
|
|
|
where I3 is a 3 ×3 identity matrix and Y is the so-called admittance matrix: |
||||||||||
Y¯ = |
|
1/jx12 + 1/jx13 |
|
−1/jx12 |
|
−1/jx13 |
|
|
||
−1/jx12 |
1/jx12 + 1/jx23 |
|
−1/jx23 |
(4.4) |
||||||
|
|
−1/jx13 |
|
−1/jx23 |
1/jx13 + 1/jx23 |
|
|
|||
2The mesh (or loop) current method is not used in this example because: (i) it can be used only for planar circuits, (ii) it is hard to implement in a computer code and, as a consequence of the previous issues, (iii) it has no relevant practical applications except for being a problem source for first-year students of electrical circuits.

4.1 Background |
63 |
More details about the admittance matrix are given in Section 11.1 of Chapter 11. For the moment, it su ces to say that this matrix can be easily built once the circuit topology is defined and that −1/z¯3 is taken apart from the admittance matrix since it does not belong to the transmission system. Since
(4.3) is linear, the solution v¯ is unique and can be obtained, for example by
¯ 3 means of an LU factorization of Y tot.
The power flow problem is conceptually the same problem as solving a steady-state ac circuit as the one shown in Figure 4.1. The only, though substantial, di erence is the set of input data. In power flow analysis, loads are expressed in terms of consumed active and reactive powers (PQ load ) and generators are defined in terms of constant voltage magnitude and active power injection (PV generator ). Finally, one generator is defined as a standard independent voltage source (i.e., as a constant voltage magnitude and phase angle) and is called slack or swing generator.
Defining one generator phase angle is needed for two reasons: (i) to fix an angle reference, and (ii) to balance system active losses. The first reason is mathematical: in ac systems, at least one phase angle has always to be assigned otherwise system equations are under-determined. For the same reason, in the branch current method discussed above, one node has to be chosen as the reference voltage level. The second reason can be explained based on a simple physical remark: one cannot fix all generator and load active powers since active power losses are not known a priori. Thus at least one active power has to be free to vary to account for transmission losses.4
In power flow analysis, it is also typical to represent the circuit as a oneline diagram as illustrated in Figure 4.2. The one-line diagram is topologically equivalent to the circuit of Figure 4.1 and implicitly assumes that generators and loads (and all shunt elements) are connected trough a common reference bus 0, which is called ground or earth.
For the system shown in Figure 4.2, one can write three complex equations (e.g., the expression of the complex power injection at each bus) or, as it is common practice to separate active and reactive power injections, six real equations. Assuming voltage polar coordinates (e.g., v¯ = vejθ ) and that the generator at bus 1 is the slack, generator at bus 2 is a PV and the load at bus 3 is a PQ, input data are: v1, θ1, p2, v2, p3 and q3. Thus, variables are p1, q1, q2, θ2, v3 and θ3.
The power flow problem is formulated in order to determine unknown voltage magnitudes and angles. Remaining unknowns, i.e., the power injections,
3In this simple example, (4.3) can be solved by hand. However practical systems have much more than three nodes and a numerical solution is thus the unique choice.
4In the example discussed in this section (see Figure 4.2), transmission lines have no resistance, thus the active power balance can be actually deduced before solving the power flow analysis. However, a loss-less transmission system is a mere approximation and is used in this example only for the sake of simplicity.
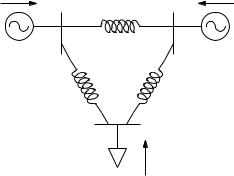
64 |
|
4 Power Flow Analysis |
s¯1 |
|
s¯2 |
1 |
|
2 |
v¯1 |
jx¯12 |
v¯2 |
|
||
jx¯13 |
|
jx¯23 |
3
v¯3
s¯3
Fig. 4.2 Classical power flow problem
can be straightforwardly computed once all bus voltages are known. In conclusion, one has to write only the equations where active or reactive power injections are known. For example, according to the rule above, the power flow equations of the system depicted in Figure 4.5 are:
0 = |
v2v1 |
sin(θ2 |
− θ1) − p2 |
|
|
(4.5) |
|||||||
x12 |
|
|
|
||||||||||
0 = |
v3v1 |
sin(θ3 |
− θ1) + |
v3v2 |
sin(θ3 − θ2) − p3 |
||||||||
x13 |
|
x23 |
|||||||||||
|
v2 |
|
|
v2 |
|
v3v1 |
|
|
|
v3v2 |
|
||
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
0 = |
|
|
+ |
|
|
− |
|
cos(θ3 − θ1) − |
|
cos(θ3 − θ2) − q3 |
|||
x13 |
x23 |
x13 |
x23 |
||||||||||
where the unknowns are v3, θ3 and θ2. It is important to note that the resulting set of equations is intrinsically nonlinear since the load at bus 3 is specified as a constant power consumption.
Equations (4.5) originate from the models of generators and loads. These models are defined based on common practice, as follows.
1.At high voltage level, loads represents an equivalent of sub-transmission systems or distribution networks. The equivalent load power consumptions can be generally well approximated as voltage dependent monomials:
pL = pL0vap |
(4.6) |
qL = qL0vaq |
|
where pL0 and qL0 are the active and reactive power consumption, respectively, at the nominal voltage. Moreover, the voltage of the equivalent load bus is typically regulated through an under load tap changer (see Chapter 14). Thus, if the voltage is maintained constant, the load can be modelled in steady-state as a constant active and reactive power consumption.

4.1 Background |
65 |
2.Synchronous generator turbine governors and automatic voltage controls are able to regulate the generated active power and the voltage at the machine bus, respectively (see Chapter 16). In steady-state, these controls can be modelled as constant p and v at the generator bus.
3.Less intuitive is the physical meaning of the slack bus, which is actually quite artificial. A slack bus is, in principle, a generator as any PV ones. However, since one active power cannot be assigned, the slack generator can only specify the voltage magnitude. Then, for similarity with all other buses where there are two unknowns, the slack generator bus is also used as reference voltage angle. Further insights and critics on the standard slack generator model are provided in Subsection 4.4.9 and in Section 10.2.2 of Chapter 10.
4.Transmission lines and transformers are generally modelled as lumped π- circuits with constant parameters (see Chapter 11).
These assumptions yield the classical power flow model. This model is nowadays so widely accepted that practically all commercial tools implement power flow equations using the assumptions discussed above. Main differences about power flow methods implemented in practice concern how variable limits (e.g., generator reactive power and load voltage limits) are handled. Another important issue is how discrete variables are handled (e.g., tap ratio of under load tap changer transformers). While these topics are detailed in Chapters 10 and 11, this chapter only focuses on power flow solution algorithms. However, it is important to note that the standard power flow model is not established by “law”. For example, there is no specific reason for assigning the reference angle at the slack generator, or for not using load and generator voltage dependent models. A very common error is to confuse common (and reasonable) model assumptions with the power flow problem itself. Furthermore, whenever possible, the solution method should not rely on the model. Last but not least, these assumptions are not unchangeable just because they are used in common commercial software packages.
In the remainder of this chapter, the power flow analysis is formulated as a general problem of finding a physical5 solution of a set of nonlinear equations. Device models are exploited only if the algorithm used for solving the power flow problem relies on them. However, one has to be aware that relying on a specific device model is a drawback of the solution method, not an advantage.
Finally, before going into the mathematical matter, let me question the power flow problem itself. Saint Agustin wrote that the doubt is the first step on the way to the truth. Thus, to question everything, especially very basic concepts, is always a good habit. The power flow analysis is actually an
5In this context, physical means acceptable. Since power flow equations are not linear, they have, generally, more than one solution. Only the solutions for which system variables are within admissible limits are of interest. Non-physical solutions of the power flow problem are further discussed in Chapter 5.
