Уровенные поверхности. Геоид и земной эллипсоид

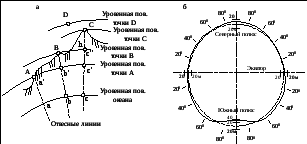
Рис. 1.1

а – уровенные поверхности; б – геоид (сплошная линия) и эллипсоид (пунктирная линия)

Из правильных математических поверхностей ближе всего к поверхностям геоида подходит эллипсоид вращения, полученный от вращения эллипса вокруг его малой оси и называемый земным эллипсоидом.

Размеры земного эллипсоида характеризуются длинами его большой аи малойбполуосей, а также сжатием,определяемым по формуле:

.

В геодезии земной эллипсоид, принятый для обработки геодезических измерений и установления системы геодезических координат, принято называть референц-эллипсоидом.

Поверхность эллипсоида и геоида близки друг к другу только в том случае, если надежно определены размеры полуосей эллипсоида вращения и эллипсоид правильно ориентирован в теле Земли. К эллипсоиду, заменяющему собой геоид, предъявляются следующие требования:

- должно быть равенство объемов геоида и эллипсоида;

- положение плоскостей экватора должно совпадать;

- должны совпадать центры тяжести геоида и эллипсоида;

- сумма квадратов отклонений эллипсоида от геоида должна быть минимальной.

В нашей стране с 1946 года используются размеры эллипсоида Красовского, уточненные с помощью спутниковой геодезии (a=6 378 245 м, 6 356 863 м). Сжатие земного эллипсоида составляет 1:298,26, а разница между экваториальным и полярным диаметрами Земли составляет 42,77 км. В том случае, когда фигуру Земли представляют в виде шара, ее радиус приближенно принимают равнымR= 6371 км.

0. 1.2 Система географических координат. Система плоских прямоугольных координат

Для определения положения точек на сфере используются географические координаты: широта и долгота, отсчитываемые от плоскости земного экватора и нулевого меридиана.

Под плоскостью земного экватора понимают плоскость, проходящую через центр Земли перпендикулярно к ее оси вращения; под плоскостью географического меридиана – плоскость, проходящую через отвесную линию и ось вращения Земли или параллельно последней. Линии пересечения плоскостей географических меридианов с поверхностью эллипсоида называются меридианами. Линии, образованные при пересечении плоскостей, проходящих перпендикулярно к оси вращения Земли, с поверхностью эллипсоида, называются параллелями. Сеть меридианов и параллелей, нанесенных определенным образом на поверхность эллипсоида, представляют собой координатные оси географической системы координат.

Под долготой понимают двугранный угол между плоскостью нулевого меридиана и плоскостью данного меридиана (точки Р); под широтой – угол, составленный отвесной линией точкиРс плоскостью экватора (рис. 1.2).

Географические координаты отдельных точек могут определяться при помощи астрономических наблюдений. Такие географические координаты принято называть астрономическими и. Положение точек на земной поверхности может также определяться с помощью географических координат, полученных из геодезических наблюдений и отнесенных к нормали к поверхности эллипсоида. Такие координаты называются геодезическими и обозначаются: широтаВ, долготаL.