2. Другие уравнения плоскости.

а) Уравнение плоскости в отрезках. Пусть в уравнении коэффициент, тогда выполним следующие преобразования

.

Введем следующие обозначения , тогда уравнение примет вид, которое называется уравнением плоскости в отрезках. Найдем точки пересечения плоскости с координатными осями:

.

Откладывая на координатных осях точки и, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметрыположительные)(Рис. 49):

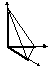
Рис. 49. Отрезки, отсекаемые плоскостью на

координатных осях.

Из рисунка видно, что числа показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.

б) Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка , через которую проходит плоскость перпендикулярно к заданному вектору.

О3. Вектор называетсянормальным вектором плоскости, если он перпендикулярен любой паре неколлинеарных векторов, лежащих на плоскости.

Возьмем на плоскости произвольную точку и образуем вектор, соединяющий точкус точкой(Рис. 50). Тогда :

Рис. 50. Плоскость, проходящая через

заданную точку перпендикулярно к

нормальному вектору.

В силу того, вектор лежит в плоскости, то он перпендикулярен нормальному вектору. Используя условие перпендикулярности векторовв проекциях перемножаемых векторов, получимуравнение плоскости: .

Пример 1. Составить уравнение плоскости, проходящей через т. параллельно плоскости.

Так как искомая плоскость параллельна плоскости , то нормальный вектор этой плоскостиперпендикулярен к искомой плоскости имо-жет быть взят в качестве нормального вектора этой плоскости. Используя уравнение плоскости, проходящей через заданную точку перпендикулярно к данному вектору, получаем: .

в) Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через три известные точки ,и. Возьмем произвольную точку плоскостии образуем вектора,и(Рис. 51):

, ,.

Рис. 51. Плоскость, проходящая через три

заданные точки.

Вектора ,икомпланарные, используя условие компланарности векторов, получимуравнение плоскости, проходящей через 3 известные точки: .

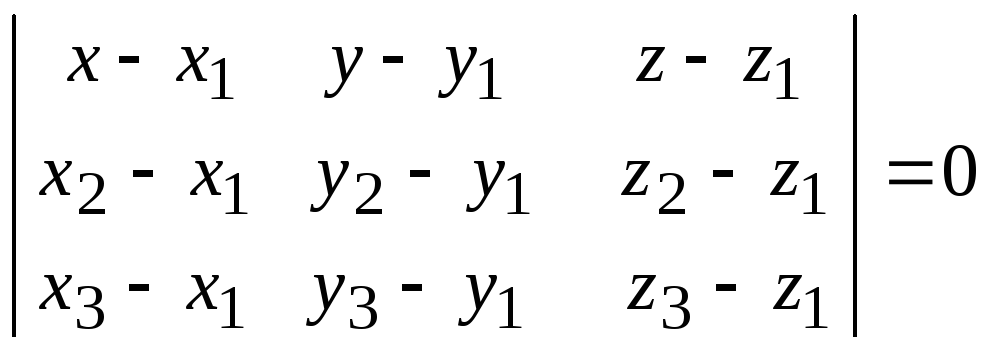З2. Полученный определитель третьего порядка раскрывается по элементам первой строки.

Пример 2. Составить уравнение плоскости, проходящей через точки

, и.

Составим определитель третьего порядка 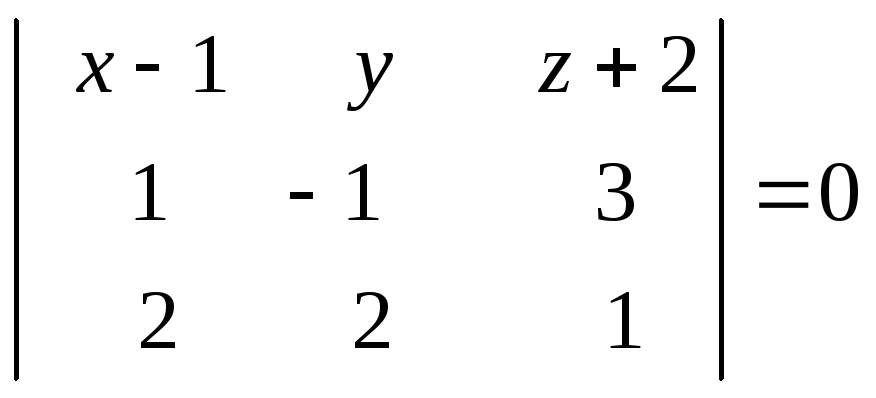. Раскроем определитель по элементам первой строки

.

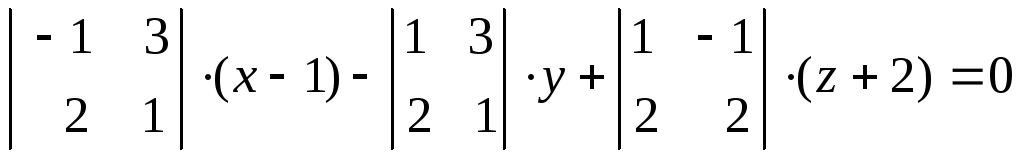Вычислим определители второго порядка: . Умножив уравнение наи раскрыв скобки, получим окончательный ответ:

.

3. Основные задачи.

а) Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости и, которые имеют нормальные вектора

и .

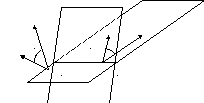
Пусть линия пересечения плоскостей определяется прямой . Из одной точ-

ки этой прямой проведем два перпендикулярных к прямой вектора и. Меньший угол между этими векторами определяет угол между плоскостями(Рис. 52):

Рис. 52. Угол между плоскос-

тями.

В силу того, что и, то угол между нормальными векторами равен углу между векторамии. Из векторной алгебры известно, что угол между векторами определяется формулой (см.Лекцию № 5):

.

Сл1. Если плоскости перпендикулярны (), то условием перпендикулярности плоскостей является равенство:

.

Сл2. Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей: .

б) Расстояние от данной точки до заданной плоскости. Расстояние от данной точки до заданной плоскостиопределяется по формуле:.

Пример 3. На каком расстоянии от плоскости находится точка.

Воспользуемся вышеприведенной формулой:

.