3. Гипербола.

О7. Гиперболой называется геометрическое место точек абсолютное значение разности расстояний от которых до двух выделенных точек и, называемых фокусами гиперболы, есть величина постоянная и равная .

Получим каноническое уравнение гиперболы. Выберем декартову систему координат так, чтобы фокусы ибыли расположены на оси абсцисс сим-метрично относительно начала отсчета. Пусть точкалежит на гиперболе, фокусы которой имеют координатыи(Рис. 31). Расстояние между фокусами (фокусное расстояние) равно . Согласно О7. для гиперболы имеем. Из треугольниковипо теореме Пифагора найдеми, соответственно. Следовательно, согласно определению имеем

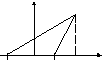
Рис. 31. Вывод уравнения гиперболы.

или .

Возведем обе части равенства в квадрат, получим

.

Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим . Раскроем разность квадратов. Подставим найденное выражение в уравнение и сократим обе части равенства на 4, тогда оно перейдет в уравнение. Вновь возведем обе части равенства в квадрат. Раскрывая все скобки в правой части уравнения, получим. Соберем неизвестные в левой части, а все известные величины перенесем в правую часть уравнения, получим. Введем обозначение для разности, стоящей в скобках. Получим

.

Разделив все члены уравнения на величину , получаемканоническое уравнение гиперболы: . Для знака “+” фокусы гиперболы расположены на оси , вдоль которой вытянута гтпербола. Для знака “–” фокусы гиперболы расположены на оси, вдоль которой вытянута гтпербола. Проанализируем полученное уравнение. Если точкапринадлежит гиперболе, то ей принадлежат и симметриичные точки,и, следовательно, гипербола симметрична относительно координат-ных осей, которые в данном случае будут называться осями симметрии гиперболы(Рис. 32). Найдем координаты точек пересечения гиперболы с координатными осями:

, т.е. точками пересечения гиперболы с осью абсцисс будут точки и;

, т.е. гипербола не пересекает ось ординат.

О8. Найденные точки иназываются вершинами ги-перболы.

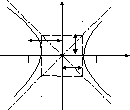
Рис. 32. Асимптоты и параметры гипер-

гиперболы.

Докажем, что при возрастании (убывании) переменной гипербола неограниченно приближается к прямым, не пересекая эти прямые. Из уравнения гиперболы находим, что. При неограниченном росте (убывании) переменнойвеличина, следовательно, гипербола будет неограниченно приближаться к прямым.

О9. Прямые, к которым неограниченно приближается график гиперболы называются асимптотами гиперболы.

В данном конкретном случае параметр называется действительной, а параметр – мнимой полуосями гиперболы.

О10. Эксцентриситетом гиперболы называется отношение фокусного

расстояния к действительной полуоси гиперболы .

Из определения эксцентриситета гиперболы следует, что он удовлетворяет

неравенству . Кроме того, эта характеристика описывает форму гиперболы. Для демонстрации этого факта рассмотрим квадрат отношения мнимой полуоси гиперболы к действительной полуоси. Если эксцентриситет, тои гипербола становится равнобочной. Если, тои гипербола вырождается в два полубесконечных отрезкаи.

Пример 2. Составить каноническое уравнение гиперболы, если мнимая полуось и гипербола проходит через точку.

Для решения задачи воспользуемся каноническим уравнением гиперболы, подставив в него все известные величины:

. Следовательно, каноническое уравнение гиперболы имеет вид .