1. Линейное д.у.

y'+P(x)y=Q(x), y,y' только в 1-й степени

2. Однородные ур-ия

y'=f()

3. Д.у. Бернулли

y'+P(x)y=Q(x)yⁿ , n=1

4. Задача Коши с нач. условием

y(x₀)=y₀ - нач. условие

5. Д.у. с разделяющимися переменными

x√y dx-(1-x²)ydy=0

6. Задачу Коши требуется решать в ур-ии

y'=2^x-y, y(-3)=5

7. Линейное д.у. решается с помощью подстановки

y=u(x)*v(x)

8. Линейным д.у. яв-ся

x²y'-2xy-3=0

9. Линейным д.У. Яв-ся

y'+ =arcsinx+x

10. Линейным д.У. Яв-ся

y'+2yx=4x²

11. Линейным д.У. Яв-ся

xy'-y=x*cosx

12. Общий вид лин. д.у. 1 порядка

y'+M(x)y=N(x)

13. Общим видом ур-ия Бернулли

y'+M(x)y=N(x)yⁿ, n не равно1

14. Однородное д.у. Решается при помощи подстановки

y= tx

15. Однородным д.у. 1 порядка яв-ся

xy'sin+x=y*sin

16. Однородным у-ем 1 порядка яв-ся

y'= (1+)/(1-)

17. Решить задачу Коши требуется в ур-нии

+e^y=0, y(1)=0

18. Ур-ием Бернулли яв-ся

y'+=-xy²

19. Ур-ием Бернулли яв-ся

xy'+y=y²lnx

20. Ур-ием Бернулли яв-ся

y'=y+x√y

21. Частное решение следует искать в ур-ии

y'+=-y², y(0)=

22. Однородным д.у. яв-ся

y'=+cos

23. Общий вид д.у. с разделенными переменными

M(x)dx+N(y)dy=0

24. Общий вид д.у. с разделяющимися переменными M₁(x)M₂(y)dx+M₂(x)N₂(y)dy

25. Общий вид д.У. С разделенными переменными

dy=dx

26. Д.У. С разделяющимися переменными

y'cosx=(y+1)sinx (y'=dy/dx)

27. Общим решением д.у. (1+x²)dy-ydx=0 яв-ся

ln|y|=arctgx+C

28. Общим решением д.у. siny*sinx*dy=cosy*cosx*dx

Csinx*cosy=1

29. Решением д.у. y'+=x яв-ся

y=+

30. Решением д.у. cosx*dx+dy=0

y=C-sinx

31. Решением д.у. y'=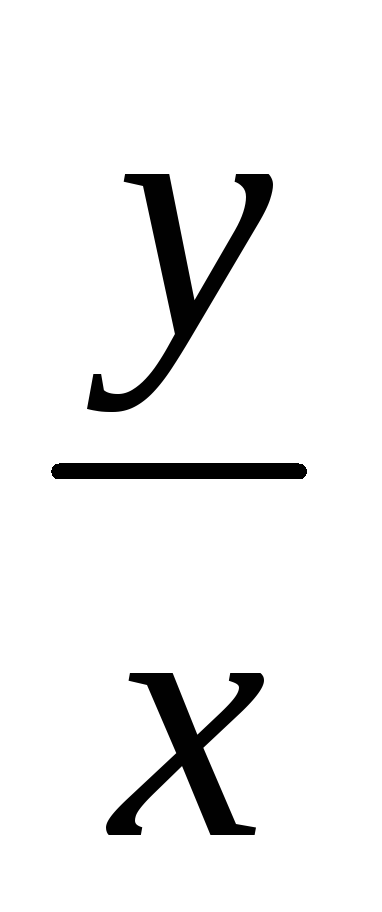+x²

y=x(C+)

32. Решением д.у. xy'=2y+2x⁴ яв-ся

y=x⁴+cx²

33. Решением д.у. y'=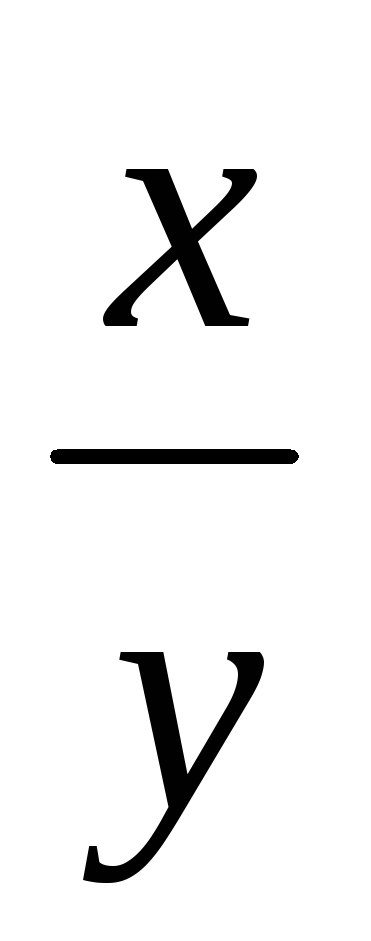+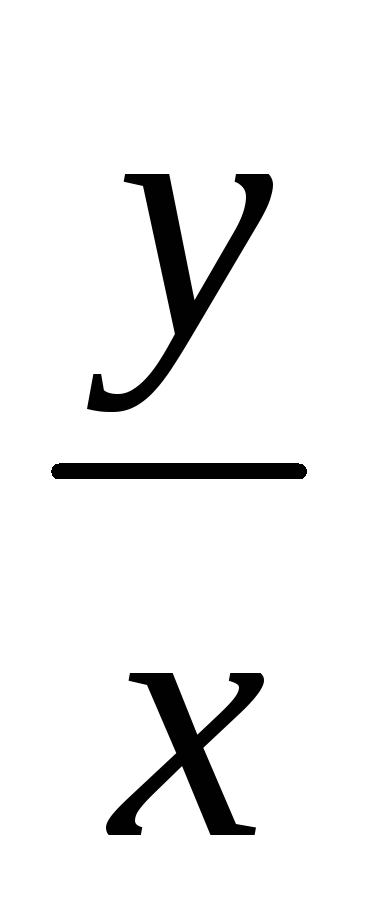яв-ся

y²=2x²ln|cx|

34. Решением ур-ия y'-=x² яв-ся

y=+Cx

35. Решением ур-ия 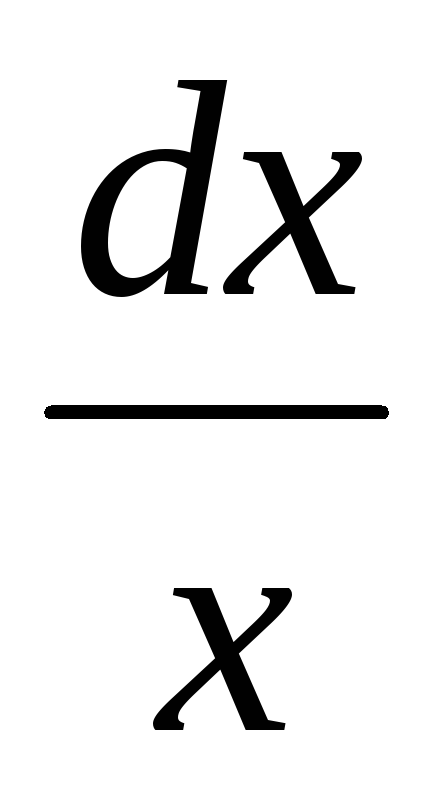-siny*dy=o яв-ся

ln|x|+cosy=C

36. Решением ур-ия y'=e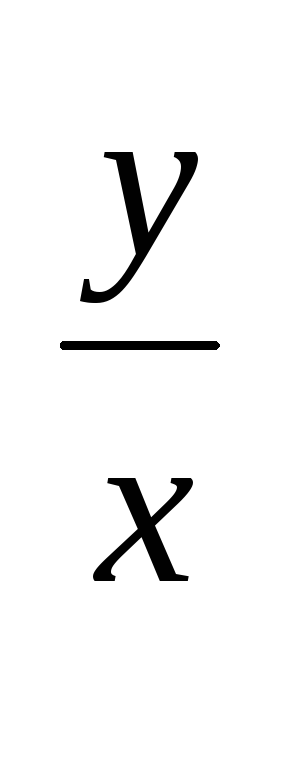+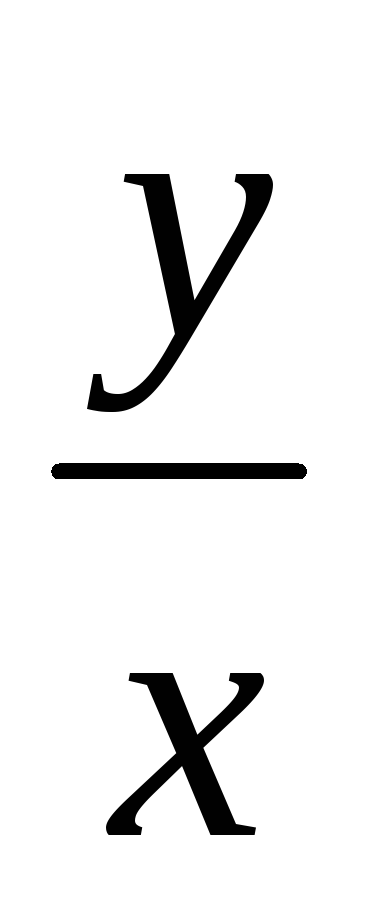яв-ся

e +ln|cx|=0

37. Решением ур-ия y'=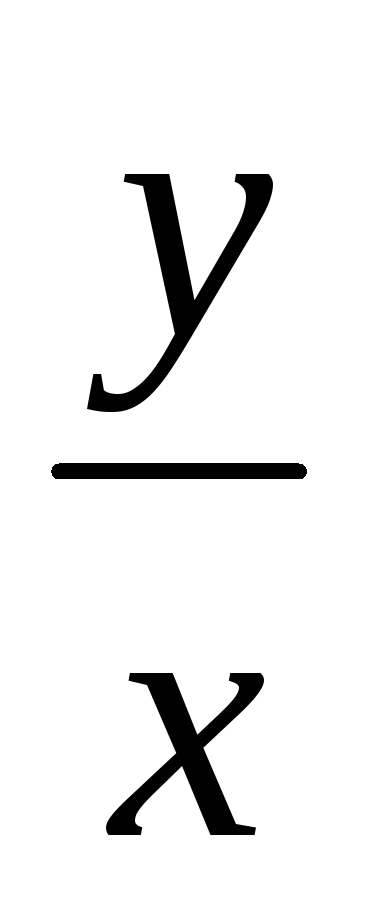+cos²яв-ся

tg=ln|cx|

38. Общим решением д.у. 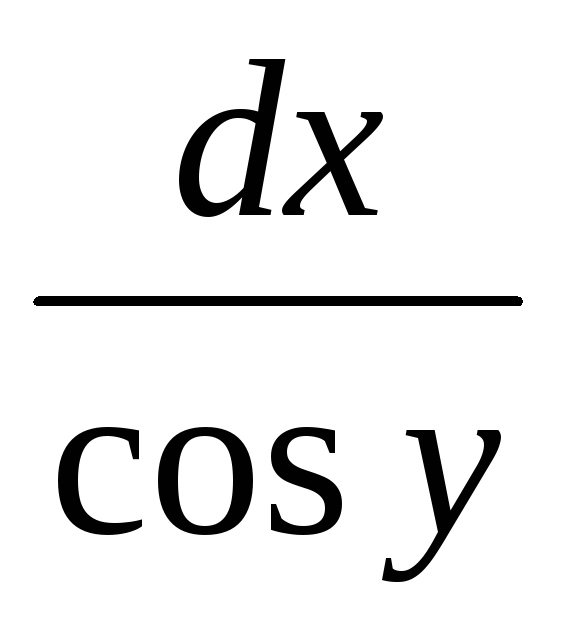- 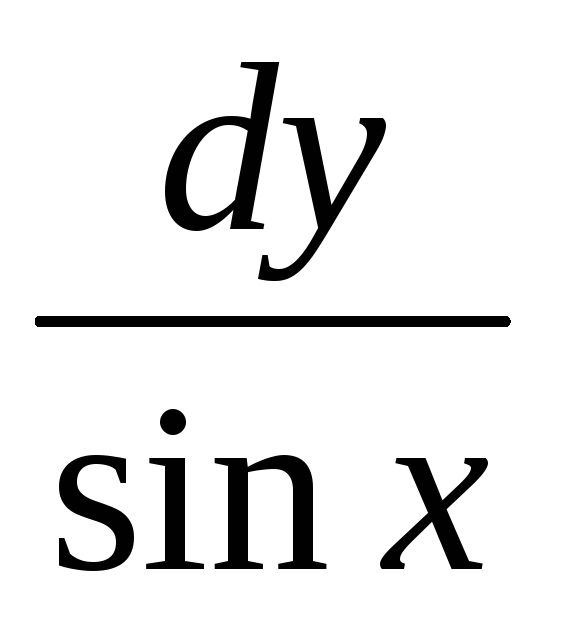=0 яв-ся

cosx+siny=С

39. Замена y'(x)=p(y) применяется в ур-ии

(y+y')*yⁿ+(y')2=0

40. Решением д.у. (xy²+x)dx+(y-x²y)dy=0

1+y²=C(1-x²)

41. Частным решением ур-ия y’=+x² при начальном условии y(1)=0.5 яв-ся

y=

42.Решением д.у. +dy=0 яв-ся

2x-3cosy=C

43. Частным решением ур-ия =, если y(1)=2 яв-ся

y=2x

44. Частным решением ур-ия -=0 при начальном условии y(1)=0 яв-ся

2=1-

45. Решением д.у. =0 яв-ся

tgx+arcsiny=C

46. Решением д.у. яв-ся

arcsinx-

47. Решением д.у. x²dx-=0 яв-ся

ln|y|=C

48. В ур-ии колебаний струны равно

49. Общим решением ур-ия яв-ся

50. Частным решением ур-ия xy’-y=xe^x при начальном условии y(1)=0 яв-ся

lnx+e=1

51. Общим решением ур-ия y’= яв-ся

y²=2x²lnCx

52. Решением д.у. xdx-y²dy=0 яв-ся

3x²-2y³=C

53. Общим решением ур-ия y’+=-xy² яв-ся

y=

54. Общим решением д.у. y¹¹-2y’-15y=0 яв-ся

y=C₁e^-3x+C₂e^5x

55. Общим решением ур-ия y’- яв-ся

y=

56. Решением д.у. dx+ яв-ся

x+2=C

57. Частным решением ур-ия y’=+x², если y(1)=0.5 яв-ся

y=