3.2 Моделирование звеньев механической системы в виде передаточных функций

В

теории автоматического регулирования разработаны, широко апробированные формальные методы составления и решения линеаризованных дифференциальных уравнений движения механических систем управления технологическими процессами в машинах и механизмах [2].Данные подходы в настоящее время широко используются при исследовании и оптимизации параметров механических систем машин и механизмов с использованием компьютеров.

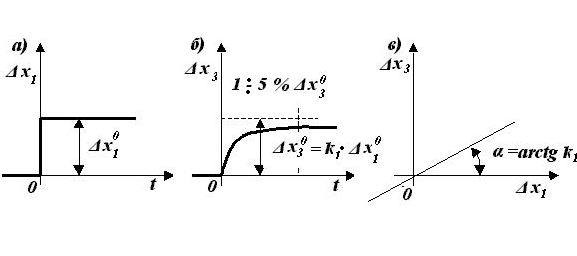
Рис. 3.4 Варианты входа механической системы

Если на вход механической подсистемы подать только постоянное значение (рис. 3.4,а) и найти установившиеся значение выходной величины, то получим . Таким образом, коэффициенты показывают отношение выходной к входной величине в установившемся состоянии.

Постоянные имеют размерность времени.

Если считать (условно) оператор дифференцирования алгебраической величиной, решим уравнение (3.7) относительно выходной величины

. (3.8)

Выражения

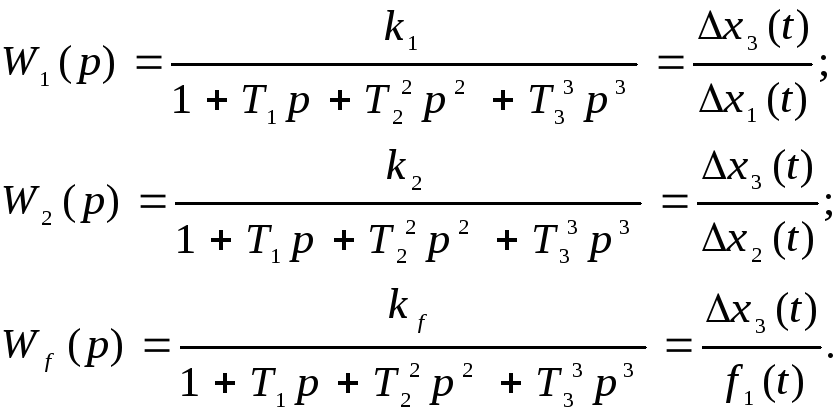
называются передаточными функциями.

Тогда уравнение (3.8) принимает вид

_{ x3(t)=W1(p)  x1(t)+ W2(p)  x2 (t)+ Wf (p) xf (t).} (3.9)

В том случае, когда отсутствуют математические модели передаточных функций, когда они не имеют аналитического выражения, их получают экспериментально. То есть, рассматривают процессы трения и, представляя их в виде передаточных функций, в выражения (3.9) вводятся изображения по Лапласу или по Карсону-Хэвисайду входных и выходных величин подсистемы

,

где -комплексная величина.

Тогда

,

при нулевых начальных условиях и равных нулю остальных воздействиях на механическую систему и .

Аналогично можно получить передаточные функции и . Поэтому, вместо дифференциального уравнения (3.9), куда входят функции времени и , можно записать при нулевых начальных условиях уравнение для изображений в виде, совпадающем по форме с (3.9)

(3.10)

В выражении (3.10) фигурируют не функции времени, а их изображения по Лапласу.

Если обозначить , то уравнение (3.10) примет вид,

, (3.11)

где - изображения функций времени по Лапласу и Карсону-Хэвисайду;

- основная круговая частота;

- оригинал функции;

- частотное изображение ;

.

Динамические свойства объекта (узла трения) могут быть определены по его переходной функции и функции веса.

Переходная функция или переходная характеристика - реакция системы на единичной воздействие (см. рис. 3.5).

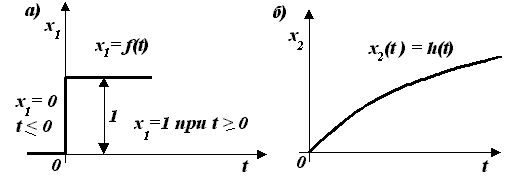
Рис. 3.5 Реакция системы на единичное воздействие

Функция веса - реакция системы на единичную импульсную функцию, поданную на ее вход (см. рис. 4.6 ).

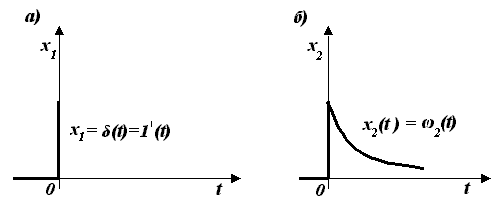
Рис. 3.6 Реакция системы на единичную импульсную функцию

,

где - дельта – функция Дирака; .

Передаточная функция есть изображение функции веса, т.е. функция веса обычно связана с его передаточной функцией преобразованием Лапласа выражением

.

Функция веса может быть получена путем дифференцирования передаточной функции по времени.

3.3 Частотные передаточные функции и частотные характеристики звеньев

Рассмотрим звено (рис. 3.7) без возмущающего воздействия, т.е. .

Рис. 3.7 Линейное звено системы

Предположим, что

,

где – амплитуда воздействия;

-угловая частота воздействия.

На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины на угол , т.е.

.(3.12)

Воспользуемся формулой Эйлера [1]

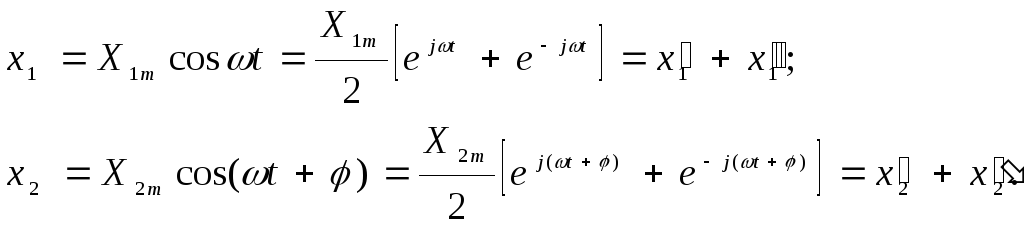
В линейных системах допускают упрощение и применяют символические записи или .

Для этих систем

. (3.13)

Воспользуемся дифференциальным уравнением звена в виде (3.7) для нахождения соотношения между входной и выходной гармоническими характеристиками

. (3.14)

Из выражения (3.13) будем иметь

.

Подставив значения входной и выходной величин и их производных в исходное дифференциальное уравнение, получим

,

откуда после сокращения на , получим

. (3.15)

Выражение (3.15) есть частотная передаточная функция объекта

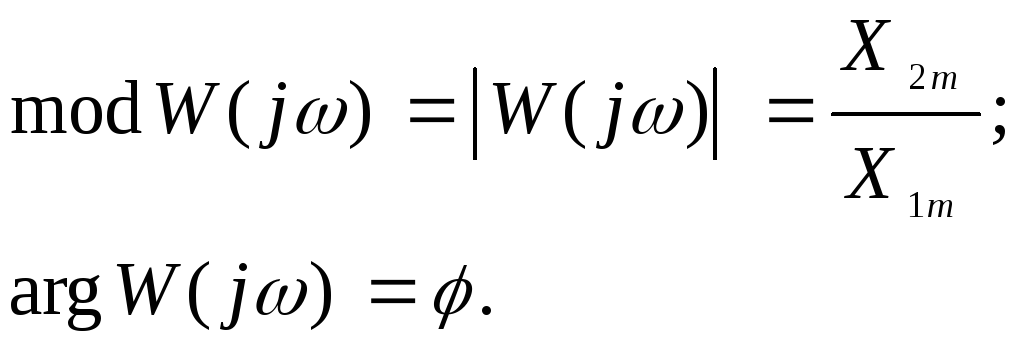
Частотная передаточная функция получается из передаточной функции подстановкой .

Частотная передаточная функция есть изображение Фурье его функции веса

. (3.16)

Частотная передаточная функция может быть представлена в следующем виде

. (3.17)

где - модуль частотной предаточной функции;

- аргумент или фаза;

вещественная и мнимая составляющая частотной передаточной функции.

Амплитудно-фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости и представляет собой геометрическое место концов векторов (годограф), соответсвующих частотной передаточной функции при изменении частоты от нуля до бесконечности (рис. 8). По оси абсцисс (см. рис. 3.8) откладывается вещественная часть , а по оси ординат –мнимая .

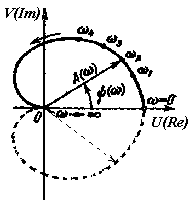
Рис. 3.8 Амплитудно – фазо – частотная характеристика

При помощи преобразования Фурье функция времени преобразуется в функцию частоты . Это означает, что функция времени представляется в виде бесконечной суммы бесконечно малых по величине векторов, вращающихся на комплексной плоскости с различными угловыми скоростями (частотами). Эта сумма определяется формулой обратного преобразования Фурье

.

Так как функция времени является вещественной, то каждому элементарному вектору , вращающемуся против часовой стрелки (), должен соответсвовать элементарный сопряженный вектор , вращающийся по часовой стрелке (). В этом случае сумма таких векторов в любой момент времени всегда вещественна. Поэтому интегрирование в формуле обратного преобразования Фурье ведется от минус бесконечности до плюс бесконечности.

Таким образом, АФЧХ дает наглядное представление об отношении амплитуд выходной и входной величин и о сдвиге фаз между ними для каждой частоты входного воздействия (рис.3.9).

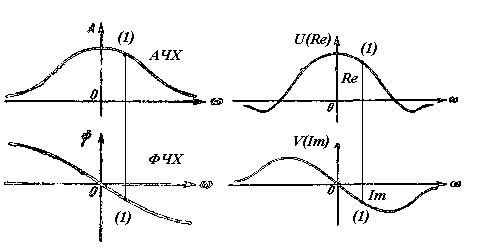
Рис. 3.9 Оценка соотношений АФЧХ