2.2.2 Принцип Даламбера

В XVIIIв. в работах Ж.-Л. Даламбера, Я. Германа и Л. Эйлера были заложены основы динамики несвободного движения, т. е. динамики движения механических систем, стесненных связями.

П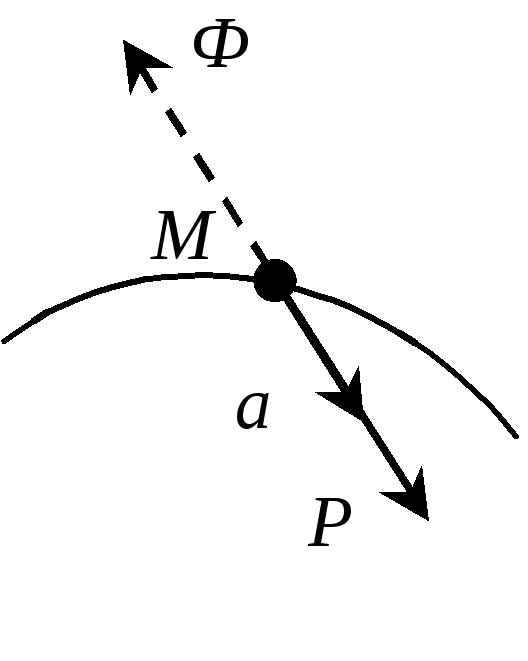режде всего, изложим принцип Даламбера для одной свободной материальной точки. Рассмотрим материальную точку , которая находится под действием активной силы (рис. 2.28).

Рис. 2.28 Модель движения материальной точки

Согласно второму закону Ньютона,

.

Перенесем член из левой части уравнения в правую и введем понятие силы инерции , тогда получим

,

или

. (2.43)

Полученное соотношение (2.43) формулируется следующим образом: геометрическая сумма приложенной к телу активной силы и силы инерции равна нулю в каждый момент времени.

Это означает, что для решения задач динамики материальной точки на основе принципа Даламбера необходимо помимо приложенной к точке M активной силы приложить к этой же точке силу инерции , обусловленную ее ускоренным движением. Уравнение (2.43) по форме совпадает с уравнениями статики и выражает уравновешенность сил и в каждый момент времени.

При изучении движения несвободной материальной точки применяют аксиому освобождаемостиот связей (была сформулирована в предыдущем праграфе), согласно которой связи, ограничивающие движениеточки, могут быть отброшены и заменены силами реакций связей таким образом, чтобы состояниеточки не изменилось.

Основное уравнение динамики для несвободной материальной точки Мпримет вид

или

,(2.44)

где – активная сила;

– реакция связей;

– сила инерции.

Уравнение (2.44) показывает, чтов любой момент времени геометрическая сумма активной силы, силы реакции связей и силы инерции для несвободной материальной точки равна нулю.Это положение называется принципом Даламбера для несвободной материальной точки. Остановимся более подробно на понятии силы инерции. Рассмотрим тело , которое лежит на гладкой горизонтальной плоскости (рис. 2.29).

Рис. 2.29 Модель движения тела по гладкой горизонтальной плоскости

Вес тела уравновешивается реакцией плоскости . Если телу сообщают ускорение с помощью нити , действующей на тело с силой , то сила инерции приложена к нити . Эту силу ощутит человек, который тянет нить. Таким образом, сила инерции является реальной силой, представляющей собой противодействие материальной точки изменению ее скорости и приложенной к телу, сообщающему этой точке ускорение. При неравномерном криволинейном движении точки силу инерции разлагают на две составляющие, направленные по касательной к траектории и по главной нормали (рис. 2.30).

Полученные составляющие и называюткасательнойинормальной силами инерции. Эти силы направлены противоположно касательному и нормальному ускорениям, поэтому

,.(2.45)

Из кинематики известно, что

,

где – алгебраическая величина скорости точки;

– радиус кривизны траектории.

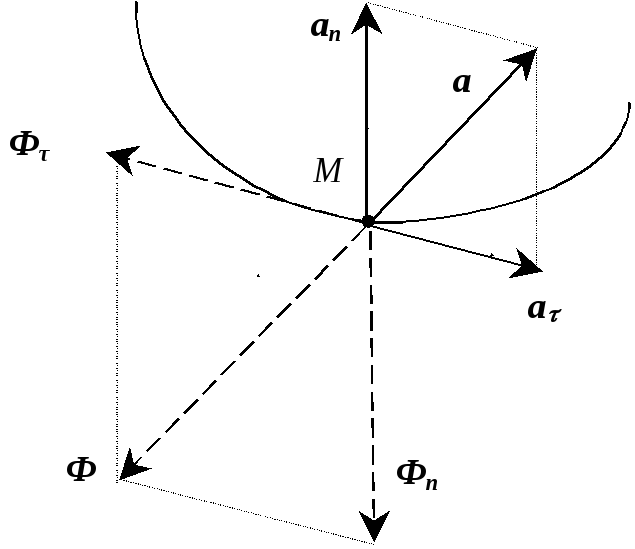
Рис. 3.30 Модель неравномерного криволинейного движения

Пользуясь этими выражениями, получаем абсолютные значения касательной и нормальной сил инерции:

,.(2.46)

Соотношение (2.45)естественным образом обобщается на случай системыnнесвободных материальных точекM_i:

, (i= 1,…,n),(2.47)

где – активная сила, приложенная к точкеM_i;

– реакция связей, ограничивающих движение точкиM_i;

– сила инерции точкиM_i.

Складывая все уравнений(2.47), получим

,(2.48)

где – главный вектор активных сил;

– главный вектор реакций связей;

– главный вектор сил инерции точек системы.

С учетом введенных обозначений (2.48)принимает вид

, (2.49)

т. е. в любой момент времени для всякой несвободной механической системы геометрическая сумма главных векторов активных сил, сил реакций связей и сил инерции материальных точек равна нулю.

Соотношение (2.49) представляет собой основу метода кинетостатики.